不相交集ADT
1.不相交集是解决等价关系的一种数据结构,执行合并和查找的速度都非常快,M次运行合并和查找的运行时间为(M*logN)。
在一个集合中,对于每一对元素(a,b),a,b∈S,对于关系R如果满足下面三个条件,则成关系R为等价关系:
(1)自反性 对于所有a∈S,aRa
(2)对称性 aRb当且仅当bRa
(3)传递性 若aRb且bRc,则aRc
2.不相交集ADT支持三种操作:
Union操作:把两个集合合并
Find操作:查找某个元素所在集合的名字,两个元素x,y在同一个集合中的充要条件是Find(x)和Find(y)返回的结果相同。
Set操作:生成若干个集合
不相交集的初始操作代码为:
void init(int a[])
{
int i;
for(i=Numsets;i>0;i--)
a[i]=-1;
}
3.不相交集的合并操作可以分为按大小合并和按高度合并。按照大小的合并,即把较小的集合合并到较大的集合中,这需要我们记录每个集合的大小。按大小合并的代码为:
void unionset(int a[],int root1,int root2)
{
int tmp=a[root1]+a[root2];
if(a[root1]<=a[root2])
{a[root2]=root1;
a[root1]=tmp;
}
else
{
a[root1]=root2;
a[root2]=tmp;
}
}
按照高度的合并是把高度较小的集合合并到高度较大的集合中,只有两个集合的高度相同是,集合的高度才会更新,这需要我们记录集合的高度,按照高度合并的代码为:
void unionset(int s[],int root1,int root2)
{
if(s[root2]<s[root1])
s[root1]=root2;
else
{
if(s[root1]==s[root2])
s[root1]--;
s[root2]=root1;
}
}
4.不相交集合的Find操作
Find操作的代码是:
int find(int a[],int x)
{
if(a[x]<=-1)
return x;
else
return find(a,a[x]);
}
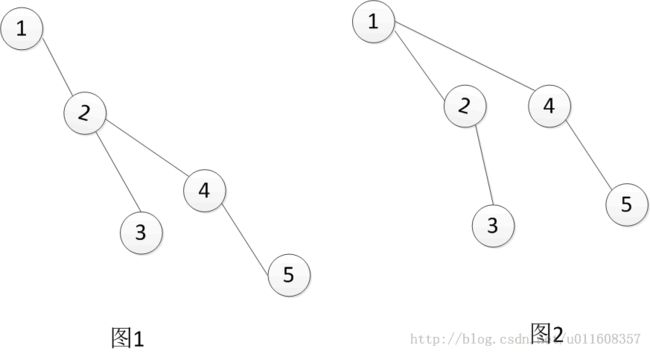
还有一种更为简便的查找方法,带有路径压缩的查找,路径压缩的效果是,从X到根的路径上的每一个结点都使它的父结点变成根。如查找5时对下面的图1集合进行路径压缩,压缩后的集合变为图2
带有路径压缩的find操作代码为:
int find(int s[],int x)
{
if(s[x]<=-1)
return x;
else
return s[x]=find(s,s[x])
}
下面是不相交集合的C语言实现:
# include <iostream>
using namespace std;
# include <stdlib.h>
int main()
{
void create(int a[],int n);
int find(int a[],int x);
void unionset(int a[],int root1,int root2);
int a[10];
create(a,10);
unionset(a,1,2);
unionset(a,2,3);
unionset(a,4,5);
cout<<find(a,5)<<endl;
system("pause");
return 0;
}
void create(int a[],int n) //不相交集的初始化
{
int i=0;
for(i=0;i<n;i++)
a[i]=-1;
}
void unionset(int a[],int root1,int root2) //合并操作,按大小合并
{
int tmp=a[root1]+a[root2];
if(a[root1]<=a[root2])
{a[root2]=root1;
a[root1]=tmp;
}
else
{
a[root1]=root2;
a[root2]=tmp;
}
}
int find(int a[],int x) //采用带有路径压缩的查找
{
if(a[x]<=-1)
return x;
else
return a[x]=find(a,a[x]);
}