[完结]saliency filters精读之permutohedral lattice
一、背景碎碎念
之前的saliency filter引用了一篇Adams的Fast high-dimensional filtering using the permutohedral lattice,2010(见引用4),看了很多遍,感觉由于篇幅受限略过去了很多东西,数学又是属于基础的问题,看起来很慢。不死心继续搜,终于功夫不负有心人,Adams在2011年写了篇HIGH-DIMENSIONAL GAUSSIAN FILTERING FOR COMPUTATIONAL PHOTOGRAPHY(Pdf),全文133页,详细介绍了Gaussian Filtering的加速方法,分两种:一个就是本篇中要详细讲的利用permutohedral lattice,第二种使用了Gaussian KD-Tree。文章还在开始处介绍了几种Gaussian滤波的家族成员:双边滤波,joint-双边滤波,joint-双边滤波upsample,以及Non-local Means。下面是高维高斯滤波的函数形式:
对于此处为什么有个1,我的理解是为了保证窗口中权值之和为1需要除一个参数,新得到rgb值缺少这么一个参数,于是就有了这个1;普通Gaussian滤波中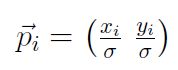 ,双边滤波中
,双边滤波中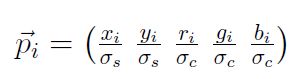 ,导致颜色迥异的点时权值近似为零。(后来我才知道这里放的两只黑狗照片是作者拍摄地,有钱淫,他的Stanford主页上还有各种旅游风景照,口水ing)这里先做简单介绍,实现代码与此有关。此后又对以上几种方法进行了图片(Canon 400D at ISO 1600.)处理的对比,发现对于非高斯噪点,joint-双边滤波对人眼表现最好,但Non-local Means处理后的照片最真实。
,导致颜色迥异的点时权值近似为零。(后来我才知道这里放的两只黑狗照片是作者拍摄地,有钱淫,他的Stanford主页上还有各种旅游风景照,口水ing)这里先做简单介绍,实现代码与此有关。此后又对以上几种方法进行了图片(Canon 400D at ISO 1600.)处理的对比,发现对于非高斯噪点,joint-双边滤波对人眼表现最好,但Non-local Means处理后的照片最真实。
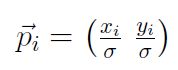 ,双边滤波中
,双边滤波中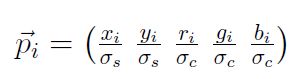 ,导致颜色迥异的点时权值近似为零。(后来我才知道这里放的两只黑狗照片是作者拍摄地,有钱淫,他的Stanford主页上还有各种旅游风景照,口水ing)这里先做简单介绍,实现代码与此有关。此后又对以上几种方法进行了图片(Canon 400D at ISO 1600.)处理的对比,发现对于非高斯噪点,joint-双边滤波对人眼表现最好,但Non-local Means处理后的照片最真实。
,导致颜色迥异的点时权值近似为零。(后来我才知道这里放的两只黑狗照片是作者拍摄地,有钱淫,他的Stanford主页上还有各种旅游风景照,口水ing)这里先做简单介绍,实现代码与此有关。此后又对以上几种方法进行了图片(Canon 400D at ISO 1600.)处理的对比,发现对于非高斯噪点,joint-双边滤波对人眼表现最好,但Non-local Means处理后的照片最真实。
下面轮到介绍本文的基本思想了,也许各位也看过了很多遍吧。。。
1)用新建坐标系,用pi表示节点坐标而不是原始的(x, y),vi保持不变
2)投影映射,就是坐标变换,降维的步骤在此处进行。一个坐标不是投影到一个点,而是类似于重心插值投影到一个单形(lattice)各个顶点处,保留各顶点的权值为以后的upsample保存。若两个不同的点投影到相同的顶点坐标时,增大此点值。
3)对lattice的顶点进行blur
4)upsample得到原始的点。
二、现有成果
由于我读本文重点在于permutohedral lattice,所以那些滤波之类的就只做了一下简单了解,joint-双边滤波-upsample和Non_local Means真心没有搞懂,这里也不瞎做介绍。然后有一幅图挺重要的,具体对比了Gaussian Filter这些年的进步。
Naive方法只是单纯地将窗口中所有点进行卷积,时间复杂度O(n^2);fast方法首先将格子中的每个点都放在了格子的重心上,时间复杂度O(nd),由于格子的个数小于point的个数,所以提速;但此方法有个缺点就是对高维Gaussian滤波不合适,产生了Improved的方法,不局限于方格而是用多项式逼近cluster的概念(此处有疑惑),双边滤波改进处就是在中心表示之后,直接对重心进行blur,然后在插值形成原来的点,时间复杂度O(d^2);本文在第一步采用了新的方法,通过提高维度的方法将格子原来的grid变成了文中的permutohedral lattice,时间复杂度也是O(d^2),但由于使用重心插值方法,能够产生更加优秀的效果;高斯Kd-tree则在分类上做了改变,有时间再继续读。
三、Permutohedral Lattice
Permutohedral lattice相比之前工作的进步之处于,
- 它不仅仅把一个点映射到格子中心表示,而是映射到lattice的各个顶点上,这样子模糊的更加精确;
- 由于每个lattice具有同等形态,能够用重心差值插值映射到lattice的各个顶点上;
- 并且能够快速在此lattice上找到映射点四周的顶点,这样子两次映射(splat,slice)能够快速进行;
- blur阶段可以每一维离散进行,并且lattice顶点能够迅速确定,此阶段能够快速进行。
一个d维的permutohedral lattice是d+1维空间中格子的所有顶点在平面中的映射。此平面法向量为1 ⃗=[1,1,…,1],所以我们有H_d: x ⃗∙1 ⃗=0。
当d=3时,lattice如上图。
此lattice的顶点坐标为整数,并且一个点的坐标各项模d+1有相同余项k,我们称之为remainder-k点。基底如下图所示。
在上一幅图中,对于一个点x ⃗=(x,y,z),当且仅当x>y>z ⋀ x-z<3时候,此点才能够在中心高亮区域。又证明了当∀x ⃗∈H_d,当max┬x ⃗ -min┬x ⃗ ≤d+1,离x ⃗最近的remainder-0点为原点,所以平面H_d中任一点只能由唯一的simplex包含,所以我们才能够放心地使用重心插值。
下面介绍利用这个permutohedral lattice进行Gauss Transform。
首先要将position点映射到超平面H_d上面,这是一个简单升维的过程。最简单的方法就是用矩阵乘法将其映射。论文中首先将每个坐标点除了一个误差,是由splat,blur以及slice中产生的。设原始坐标p ⃗除以√(2/3) (d+1)得到x ⃗,乘以矩阵E映射到高维空间。
举例bilateral filter,position由5-D向量组成,
首先要将position点映射到超平面H_d上面,这是一个简单升维的过程。最简单的方法就是用矩阵乘法将其映射。论文中首先将每个坐标点除了一个误差,是由splat,blur以及slice中产生的。设原始坐标p ⃗除以√(2/3) (d+1)得到x ⃗,乘以矩阵E映射到高维空间。
举例bilateral filter,position由5-D向量组成,
计算方法如下:
Splat阶段:
使用rounding algorithm找到最近的remainder-0点,然后平移至标准单元形中找到simplex剩余顶点。
找到离平移Ex ⃗至以原点为remainder-0的标准单元形中y ⃗点,计算重心权重b,查找哈希表将此y ⃗点的value乘以顶点(v_j ) ⃗相应b_j,再加到(v_j ) ⃗点的值(u_j ) ⃗上,有如下形式:
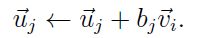
使用rounding algorithm找到最近的remainder-0点,然后平移至标准单元形中找到simplex剩余顶点。
找到离平移Ex ⃗至以原点为remainder-0的标准单元形中y ⃗点,计算重心权重b,查找哈希表将此y ⃗点的value乘以顶点(v_j ) ⃗相应b_j,再加到(v_j ) ⃗点的值(u_j ) ⃗上,有如下形式:
将和的索引储存至一个新table的位置(i, j)上,以便后续查找。
Blur阶段:
循环查找哈希表中每一点取值(v_old) ⃗,在哈希表中再次找到它position±[1,1,…,d,1,…,1]的结点,取值(v1) ⃗,(v2) ⃗。做加法(v_new) ⃗=(v1) ⃗+(v2) ⃗+2*(v_old) ⃗,放入原位置。假设哈希表长度为l,每个结点需要查找O(d)次邻居节点,每次用时O(d),所以此步骤用时为O(ld^2)。
循环查找哈希表中每一点取值(v_old) ⃗,在哈希表中再次找到它position±[1,1,…,d,1,…,1]的结点,取值(v1) ⃗,(v2) ⃗。做加法(v_new) ⃗=(v1) ⃗+(v2) ⃗+2*(v_old) ⃗,放入原位置。假设哈希表长度为l,每个结点需要查找O(d)次邻居节点,每次用时O(d),所以此步骤用时为O(ld^2)。
Slice阶段:
同splat阶段步骤,利用权重b计算插值。由于在splat阶段建立了b的table,所以用时O(nd)。
本算法总计用时为O((n+l)d^2)。
此图为速度比的等高线,为最快速度和第二快的算法结构用时之比。颜色越深相差越大。图片左侧标志维度,横轴为filter size,右侧为使用的算法。
可以看到5-20维度时候permutohedral lattice根据filter size情况最优。
可以看到5-20维度时候permutohedral lattice根据filter size情况最优。
完结。
![[完结]saliency filters精读之permutohedral lattice_第1张图片](http://img.e-com-net.com/image/info5/7834a5bd3aa64a4bb4a4906dcd654cac.jpg)
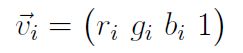
![[完结]saliency filters精读之permutohedral lattice_第2张图片](http://img.e-com-net.com/image/info5/cbdf8f426990470fb6dd86840bbbb750.jpg)
![[完结]saliency filters精读之permutohedral lattice_第3张图片](http://img.e-com-net.com/image/info5/4ace7a94d8344a908b01c6c2601aa0cd.png)

![[完结]saliency filters精读之permutohedral lattice_第4张图片](http://img.e-com-net.com/image/info5/289b012499db4d179a4c7e466482a0b8.jpg)
![[完结]saliency filters精读之permutohedral lattice_第5张图片](http://img.e-com-net.com/image/info5/593e668003cc4a57a8b4461c3302ceed.jpg)