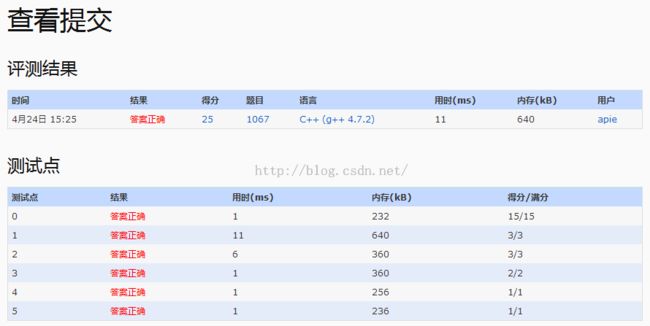
1067. Sort with Swap(0,*) (25)

题目链接：http://www.patest.cn/contests/pat-a-practise/1067

题目：

Given any permutation of the numbers {0, 1, 2,..., N-1}, it is easy to sort them in increasing order. But what if Swap(0, *) is the ONLY operation that is allowed to use? For example, to sort {4, 0, 2, 1, 3} we may apply the swap operations in the following way:

Swap(0, 1) => {4, 1, 2, 0, 3}
Swap(0, 3) => {4, 1, 2, 3, 0}
Swap(0, 4) => {0, 1, 2, 3, 4}

Now you are asked to find the minimum number of swaps need to sort the given permutation of the first N nonnegative integers.

Input Specification:

Each input file contains one test case, which gives a positive N (<=10⁵) followed by a permutation sequence of {0, 1, ..., N-1}. All the numbers in a line are separated by a space.

Output Specification:

For each case, simply print in a line the minimum number of swaps need to sort the given permutation.

Sample Input:

10 3 5 7 2 6 4 9 0 8 1

Sample Output:

9

分析：

基数排序，因为是0,N-1所以每个数字都知道其对应的位置，把相应的数字放到正确的位置上去的步骤就是最短的步骤

对于一个数组中的数字，有三种情况
1），它在正确的位置，那么不用动

2），如果它在错误的位置，那么和它在同一组的数字有num个，并且其中如果包括0，那么只需要n - 1次这num个数都能回到自己的正确位置上

3），如果它在错误的位置，那么和它在同一组的数字有num个，并且其中如果不包括0，那么需要n +1次这num个数才能回到自己的正确位置上（相当于需要先把0和其中一个数字对调，最后再把0对调回0位置，所以增加了两次）

比如0，2，1，3这四个数字，0，3在正确的位置上，2，1它们两个是一组的，因为都占了其他的正确的位置，所以这里num = 2，并且需要2+1=3次才能把全部都调对。

比如0，4，3，2，1这五个数字，0是在正确的位置上，而4和1是一组，3和2是一组，它们都需要3次，所以总共需要6次才能把他们排好序。

比如3 5 7 2 6 4 9 0 8 1这10个数字，其中8在正确的位置上，而3 7 2 0这四个为一组，他们需要3次，5，6，4，9，1为一组，它们需要6次，所以总共需要9次。

至于怎么找出一个不在正确位置上的数所在组的其他数字，可以采用类似基数排序的方式，把它所在位置上的数字和其数字所对应位置上的数字对调，知道所调回的数和自己的位置对应上，这个次数 + 1就是所在组的数字数目了。

AC代码：

#include<stdio.h> 
int main(void){ 
 freopen("F://Temp/input.txt", "r", stdin); 
 int n; 
 scanf("%d", &n); 
 int *input = new int[n]; 
 for (int i = 0; i < n; i++){ 
  scanf("%d", (input + i)); 
 } 
 int count = 0; 
 bool flag = false; 
 if (*input == 0)flag = true;//flag表示第一位是不是0 
 int group_num = 0;//组数目 
 for (int i = 0; i < n; i++){ 
  bool newGroup = false; 
  while (*(input + i) != i){ 
   newGroup = true; 
   int tmp = *(input + *(input + i)); 
   *(input + *(input + i)) = *(input + i); 
   *(input + i) = tmp; 
   count++; 
  } 
  if (newGroup)group_num++; 
 } 
 if (flag)count += group_num * 2; 
 else{ 
  count += (group_num - 1) * 2; 
 } 
 printf("%d\n", count); 
 return 0; 
}

截图：

——Apie陈小旭