回归分析之线性回归

1回归分析

1.1概念

回归分析（英语：Regression Analysis）是一种统计学上分析数据的方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便观察特定变量来预测研究者感兴趣的变量。

运用十分广泛，回归分析按照涉及的自变量的多少，可分为 一元回归分析和 多元回归分析；按照 自变量和 因变量之间的关系类型，可分为 线性回归分析和 非线性回归分析。如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是 线性关系，则称为 多元线性回归分析。

回归分析的一般流程是：
（1）确定Y与X间的定量关系表达式，这种表达式称为回归方程；
（2）对求得的回归方程的可信度进行检验；
（3）判断自变量X对因变量Y有无影响；
（4）利用所求得的回归方程进行预测和控制。

1.2 效果分析-统计检验

主要有拟合优度检验R^2，显著性检验T， 显著性检验F。

R    R^2表示的是拟合优度，它是用来衡量估计的模型对观测值的拟合程度。它的值越接近1说明模型越好。
F的值是回归方程的显著性检验，表示的是模型中被解释变量与所有解释变量之间的线性关系在总体上是否显著做出推断。若F>Fa(k-1,n-k),则拒绝原假设，即认为列入模型的各个解释变量联合起来对被解释变量有显著影响，反之，则无显著影响。

T的数值表示的是对单个回归参数的显著性检验值，它的绝对值大于等于ta/2(n-k)（这个值表示的是根据你的置信水平，自由度得出的数值）时，就拒绝原假设，即认为在其他解释变量不变的情况下，解释变量X对被解释变量Y的影响是显著的。

参考自： http://course.cug.edu.cn/cugThird/Econometrics/Chapter_study/chapter_3_2.htm

2 线性回归

2.1概念

本质上建立变量之间的线性关系，表现形式就是线性方程y=ax+b,例如给出两组数据x={0, 1, 2, 3, 4, 5}, y={0, 20, 60, 68, 77, 110}，拟合出直线。线性回归模型经常用最小二乘逼近来拟合。

线性回归是利用 数理统计 中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种 统计分析 方法，运用十分广泛。分析按照 自变量 和 因变量 之间的关系类型，可分为线性回归分析和非线性回归分析。 在 统计学 中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个 自变量 和 因变量 之间关系进行建模的一种 回归分析 。

线性回归模型经常用最小二乘逼近来拟合，但他们也可能用别的方法来拟合，比如用最小化“拟合缺陷”在一些其他规范里（比如最小绝对误差回归），或者在桥回归中最小化最小二乘损失函数的惩罚.相反,最小二乘逼近可以用来拟合那些非线性的模型.因此，尽管“最小二乘法”和“线性模型”是紧密相连的，但他们是不能划等号的

2.2用途

线性回归有很多实际用途。分为以下两大类：
如果目标是预测或者映射，线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。
给定一个变量y和一些变量X1,...,Xp，这些变量有可能与y相关，线性回归分析可以用来量化y与Xj之间相关性的强度，评估出与y不相关的Xj，并识别出哪些Xj的子集包含了关于y的冗余信息。

2.3假设检验

线性关系： Y=A+BX+§
式中：A和B为待定参数，A为 回归直线的截距；B为回归直线的斜率，表示X变化一个单位时，Y的平均变化情况；§为依赖于用户满意度的 随机误差项。
对于经验回归方程： y=0.857+0.836x
回归直线在y轴上的截距为0.857、斜率0.836，即质量每提高一分，用户满意度平均上升0.836分；或者说质量每提高1分对用户满意度的贡献是0.836分。
上面所示的例子是简单的一个自变量的线性回归问题，在数据分析的时候，也可以将此推广到多个自变量的多元回归，具体的回归过程和意义请参考相关的 统计学书籍。此外，在SPSS的结果输出里，还可以汇报R2，F检验值和T检验值。R2又称为方程的确定性系数（coefficient of determination），表示方程中变量X对Y的解释程度。R2取值在0到1之间，越接近1，表明方程中X对Y的解释能力越强。通常将R2乘以100%来表示回归方程解释Y变化的百分比。F检验是通过 方差分析表输出的，通过显著性水平（significant level）检验回归方程的线性关系是否显著。一般来说，显著性水平在0.05以上，均有意义。当F检验通过时，意味着方程中至少有一个回归系数是显著的，但是并不一定所有的回归系数都是显著的，这样就需要通过T检验来验证回归系数的显著性。同样地，T检验可以通过显著性水平或查表来确定。在上面所示的例子中，各参数的意义如表8－2所示。
线性回归方程检验

指标	显著性水平	意义
R2	0.89		“质量”解释了89%的“用户满意度”的变化程度
F	276.82	0.001	回归方程的线性关系显著
T	16.64	0.001	回归方程的系数显著

示例 SIM手机用户满意度与相关变量线性回归分析
我们以SIM手机的用户满意度与相关变量的线性回归分析为例，来进一步说明线性回归的应用。从实践意义讲上，手机的用户满意度应该与产品的质量、价格和形象有关，因此我们以“用户满意度”为因变量，“质量”、“形象”和“价格”为自变量，作线性回归分析。利用SPSS软件的回归分析，得到回归方程如下：
用户满意度=0.008×形象+0.645×质量+0.221×价格
对于SIM手机来说，质量对其用户满意度的贡献比较大，质量每提高1分，用户满意度将提高0.645分；其次是价格，用户对价格的评价每提高1分，其满意度将提高0.221分；而形象对产品用户满意度的贡献相对较小，形象每提高1分，用户满意度仅提高0.008分。
方程各检验指标及含义如下：

指标	显著性水平	意义
R2	0.89		“质量”和“形象”解释了89%的“用户满意度”的变化程度
F	248.53	0.001	回归方程的线性关系显著
T（形象）	0.00	1.000	“形象”变量对回归方程几乎没有贡献
T（质量）	13.93	0.001	“质量”对回归方程有很大贡献
T（价格）	5.00	0.001	“价格”对回归方程有很大贡献

3 最小二乘

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

在我们研究两个 变量（x,y）之间的相互关系时，通常可以得到一系列成对的数据（x1,y1.x2,y2... xm,ym）；将这些数据描绘在x -y直角坐标系中，若发现这些点在一条直线附近，可以令这条 直线方程如（式1-1）。

其中：a0、a1 是任意实数

为建立这直线方程就要确定a0和a1，应用《最小二乘法原理》，将实测值Yi与利用（式1-1）计算值（Yj=a0+a1X）的离差（Yi-Yj）的平方和

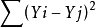 最小为“优化判据”。

令：φ =

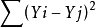 （式1-2)

把（式1-1）代入（式1-2）中得：

φ =

 （式1-3)

当

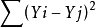 最小时，可用函数 φ 对a0、a1求偏导数，令这两个 偏导数等于零。

∑2（a0 + a1*Xi - Yi）（式1-4)

∑2*Xi（a0 + a1*Xi - Yi）（式1-5)

亦即：

na0 + （∑Xi ) a1 = ∑Yi （式1-6)

（∑Xi ) a0 + （∑Xi^2 ) a1 = ∑（Xi*Yi) （式1-7)

得到的两个关于a0、 a1为未知数的两个方程组，解这两个方程组得出：

a0 = （∑Yi) / n - a1（∑Xi) / n （式1-8)

a1 = [n∑Xi Yi - （∑Xi ∑Yi)] / [n∑Xi2 - （∑Xi)2 )] （式1-9)

这时把a0、a1代入（式1-1）中， 此时的(式1-1）就是我们回归的元线性方程即：数学模型。

在回归过程中，回归的关联式不可能全部通过每个回归数据点（x1,y1. x2,y2...xm,ym），为了判断关联式的好坏，可借助 相关系数“R”， 统计量“F”，剩余标准偏差“S”进行判断；“R”越趋近于 1 越好；“F”的绝对值越大越好；“S”越趋近于 0 越好。

R = [∑XiYi - m （∑Xi / m）（∑Yi / m)]/ SQR{[∑Xi2 - m （∑Xi / m)2][∑Yi2 - m （∑Yi / m)2]} （式1-10) *

在（式1-10）中，m为 样本容量，即实验次数；Xi、Yi分别为任意一组实验数据X、Y的数值。