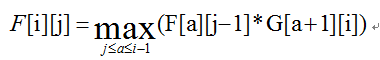- #19ACM第三次周赛补题赛de题解呐#
桦hua呐
秃头hua的题解
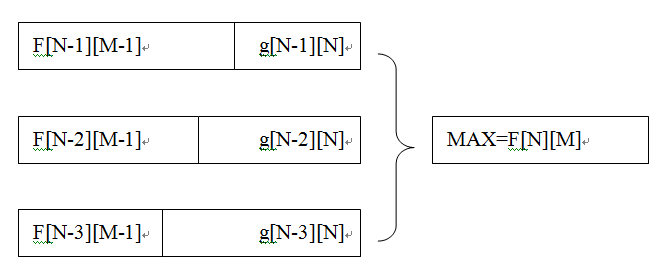
我真的太low了,谁能教教我C.D.E.?A.我是个签到题!这题的确签到,一共y/n两种情况,运气不好WA一次,运气好直接过,但相信聪明的你们,一定去探索了方程式的规律,才不会像我一样盲猜n就对了,嘿嘿,看题↓描述:判断x^4+y^4=z^4,x,y,z是否存在正整数解输入:无输出:存在输出“YES”,不存在输出"NO"直接送上hua的无脑代码↓#includeintmain(){printf("
- #19ACM第五次周赛补题赛de题解呐#
桦hua呐
秃头hua的题解
磕出来的所有题唉……A.防AK题目——超难系列这是一道Helloword题,题面花里胡哨,但就想让你输出一个“Accepted!!!”。#includeintmain(){printf("Accepted!!!");return0;}B.Fenoix超厌恶xxx这一题呢判断几种可能情况来进行即可,先看题面:描述:Fenoix觉得xxx是一个非常怪的人,因为他特别厌恶xxx这样的人。现在他给你出一道
- Android Telephony 网络状态中的 NAS 信息
Dic-
#AndroidTelephony#计算机网络网络通信Telephony自学笔记Android计算机网络移动网络非接入层
引言上层如何拿到NAS信息?那么首先要知道什么是NAS。领域知识术语表通信网络术语英文缩写英文全称中文含义NASNon-AccessStratum非接入层RRCRadioResourceControl无线资源控制层PDCPPacketDataConvergenceProtocol分组数据汇聚协议层RLCRadioLinkControl无线链路控制层MACMediumAccessControl媒体接
- HDU杭电OJ基础100题2010-2019(C语言版)
雁于飞
算法专栏c语言开发语言
文章目录@[TOC](文章目录)[原题出处](https://acm.hdu.edu.cn/listproblem.php?vol=11)前言p2010.水仙花数问题描述解题思路代码核心思想:p2011多项式求和问题描述代码p2003求绝对值问题描述解题思路代码扩展p2004成绩转换问题描述解题思路代码重点p2005第几天问题描述解题思路代码扩展p2006求奇数的乘积p2007平方和与立方和问题描
- WIN11+VSCODE搭建的c/c++环境调试报错解决
xtmatao
C语言编程vscodec语言c++
解决调试报错前面win11+vscode搭建的c/c++环境,ctrl+shift+B生成正常,cttl+F5运行正常。今天打断点逐步调试时报错,提示找不到库文件。解决方案如下:下载mingw-w64源码库:(两种途径)通过MSYS2UCRT64终端下载pacman-Sgit#安装gitgitclonehttps://git.code.sf.net/p/mingw-w64/mingw-w64#下载
- 手动续期证书后自动上传到阿里云
要将acme.sh续期后的脚本自动传到阿里云上,可以按照以下步骤进行:安装阿里云CLI:在服务器上安装阿里云命令行工具(CLI),以便能够通过命令行与阿里云进行交互。可以使用以下命令进行安装:wgethttps://aliyuncli.alicdn.com/aliyun-cli-linux-latest-amd64.tgz&&tarxzvfaliyun-cli-linux-latest-amd64
- Mac mini 跑 DeepSeek R1 及 QwQ-32B模型实测报告
强哥之神
GPTmacosGPUdeepseek人工智能语言模型LLM
测试对象:2025款Macmini(M4/M4Pro芯片)测试模型:DeepSeek-R1(14B/32B)、QwQ-32B(原版/量化版)测试目标:硬件性能适配性、推理速度、内存占用及优化方案一、Macmini硬件配置概览配置项M4基础款(16GB)M4Pro高配(32GB/64GB)芯片M4(10核CPU/10核GPU)M4Pro(14核CPU/20核GPU)内存16GB统一内存32GB/64
- 项目实战复盘:跨平台团队如何组合工具完成 iOS App 上架全流程
2501_91600889
httpudphttpswebsocket网络安全网络协议tcp/ip
在一次使用Flutter开发的跨平台项目中,我们团队要将一款教育类App同时上线Android与iOS。团队成员清一色Windows/Linux用户,仅有远程使用的一台旧款Macmini,资源非常有限。这篇文章将还原我们当时iOS上架的完整流程,并分享我们是如何组合使用不同工具,各自完成关键环节,不依赖完整Mac环境也能顺利上线AppStore的经验。阶段一:准备开发者证书和描述文件(Provis
- acme自签证书
获取acme自签证书1、安装安装acmegitclonehttps://gitee.com/neilpang/acme.sh.gitcdacme.sh./
[email protected]、获取阿里云ak/sk3、生成证书通过环境变量导入ak/skexportAli_Key="控制台获取ak"exportAli_Secret="控制台获取sk"生成证书(有效期3个月
- 【题解】洛谷P1001 A+B Problem
炯炯目光
c++
写在前面第一篇博客,献给2020年的残夏。静听8月的热情与安宁,在竞赛中的时光如白驹过隙。也不惧未知的风雨,努力向着既往的通途。ACMACMACM的目标,希望能实现吧。同时,推荐一下我的个人博客,欢迎访问。https://www.cnblogs.com/jjmg/下面是页面编辑的测试。题目地址https://www.luogu.com.cn/problem/P1001题目描述输入两个整数a,ba,
- 信息检索简介——文本处理、搜索引擎、数据挖掘、机器学习、推荐系统等
AI天才研究院
Python实战自然语言处理人工智能语言模型编程实践开发语言架构设计
作者:禅与计算机程序设计艺术1.简介2005年8月17日至9月3日在美国加利福尼亚州伯克莱纳举行了SIGIR国际会议(中文全称“计算机信息retrieval国际会议”),这是信息检索领域的顶级会议之一。该会议由ACM主办,主题涵盖了包括文本处理、搜索引擎、数据挖掘、机器学习、推荐系统等多个热门方向。此次会议是第一次将信息检索作为一个学科,并取得重大突破。本文试图对SIGIR进行一个完整的介绍,阐述
- abp 链接本地mysql_ABP Vnext使用mysql数据库
漫小威
abp链接本地mysql
ABPVnext支持Sqlserver、Mysql、PostgreSql等数据库,通过CLI模板建立的项目默认使用SqlServer,需要进行一定变更才支持其他数据库,下面以使用Mysql举例1.使用CLI建立一个带UI的MVC项目abpnewAcme.BookStoreUi--templateapp--database-provideref--uimvc--mobilenone建立后项目如下2.
- 重温经典第二弹(xdoj1175,xdoj1179)
Owen_Q
搜索暴力枚举字符串
一转眼,记忆又来到了暑假。或许,这是一个这算是自己真正开始接触了解acm的一个时间点吧,各种算法数据结构,开始慢慢浮出水面。回顾当初,感慨万千。又找出了两道未ac之题,确实复杂度明显加强,思维性的进一步考验。Count思路:子串搜索问题,因为n和k大到2e5,因此,肯定是个单向处理不能回溯的问题,否则最坏n方的复杂度是难以接受的。对于单次搜索,考虑可以维护现有区间的元素,然后移位遍历向后搜索,对于
- ACM ICPC 2017 Warmup Contest 7(CTU Open Contest 2016)
Owen_Q
水题搜索数组stlacm
ccsp与区域赛都越来越近了,模拟与区域赛题并进,还有一堆作业,有点累,想玩耍,感觉自己有点迷失,算了,还是就这样吧,努力向前练习赛7,打两个签到题走人,继续刷csp去B.HotAirBallooning思路:统计不同人用过的气球的方案数,又是个去重问题,又想往set上放,后来发现气球数很少,完全可以数组统计,而气球总组合有限,虽然不大,但强搜可能会感觉tle,加个状压好了,感觉现在自己特别喜欢做
- 008 【入门】算法和数据结构简介
要天天开心啊
算法专栏算法数据结构
算法与数据结构系统概览|[算法]-[基础]-[通用]一、算法分类与应用1.硬计算类算法|[算法]-[中级]-[通用]特点应用场景复杂度特征-精确求解问题-可能带来较高计算复杂度-大厂笔试/面试-ACM竞赛-所有程序员岗位必考⏱️通常为O(n)~O(n²)//[示例]快速排序算法-分治思想核心实现publicvoidquickSort(int[]arr,intleft,intright){if(le
- 【Linux】ghb工具
nanguochenchuan
Linux操作系统linux运维服务器
GDB简介GDB(GNUDebugger)是Linux系统中最强大的命令行调试工具,由GNU项目开发。作为程序员调试C/C++程序的利器,GDB能帮助你:定位程序崩溃原因分析程序运行状态跟踪变量值变化检测内存错误安装与配置安装方法#Ubuntu/Debiansudoaptinstallgdb#CentOS/RHELsudoyuminstallgdb#ArchLinuxsudopacman-Sgdb
- 中国计算机学会推荐国际学术会议-体系结构相关(含投稿截至时间)
HiAallen
事务编辑器
Ref:CCF推荐国际学术刊物目录-中国计算机学会中国计算机学会推荐国际学术会议(●计算机体系结构/并行与分布计算/存储系统)A类序号刊物名称刊物全称出版社投稿截止时间地址1PPoPPACMSIGPLANSymposiumonPrinciples&PracticeofParallelProgrammingACM2022-8-17dblp:PPOPP2FASTConferenceonFileandS
- 2019 CCF 推荐国际学术期刊&会议(计算机体系结构/并行与分布计算/存储系统)
漓艾初
CCF
中国计算机学会推荐国际学术期刊&会议直接去这里找,全部都有https://www.ccf.org.cn/Academic_Evaluation/By_category/计算机体系结构/并行与分布计算/存储系统期刊A类序号刊物简称刊物全称出版社网址1TOCSACMTransactionsonComputerSystemsACMhttp://dblp.uni-trier.de/db/journals/
- manjaro安装微软雅黑字体_开始使用 Manjaro(添加源+字体渲染去模糊+软件安装+优化配置+常见错误)(30)...
真的是单大宝
manjaro安装微软雅黑字体
1.添加archlinux镜像源1.步骤一向/etc/pacman.d/mirrorlist中添加国内镜像地址1.1方法1:自动添加1、输入如下命令查看国内镜像源,并按质量排序:sudopacman-mirrors-i-cChina-mrank,之后会弹出一个窗口,可以选择想要的镜像源,选择确定后会自动导入/etc/pacman.d/mirrorlist配置文件中。1.2方法2:手动添加直接在et
- iOS App 上架流程工具链解析:开发者视角下的协作实践总结
2501_91591841
httpudphttpswebsocket网络安全网络协议tcp/ip
在我们最近完成的一个B2C健康管理类App项目中,有一个显著的特点:开发团队并不拥有统一的macOS环境。我们使用Flutter开发,一部分成员使用Windows,一部分使用Ubuntu,团队中仅有一台远程可用的Macmini作为打包主机。这次项目的iOS上架过程从准备证书、打包构建、上传提交,到信息维护与测试,每一个步骤都涉及多个工具协作。本文是从一个工程师的日常视角,拆解我们如何组合各类工具完
- Ubuntu22.04安装CH343驱动并创建udev规则
驱动说明Linux系统提供CH34*系列USBUART设备配合使用的默认CDC-ACM驱动程序。驱动程序文件名为CDC-ACM。CDC-ACM驱动程序控制特定设备的能力有限。此通用驱动程序不了解特定设备协议。因此,设备制造商可以创建能够访问设备特定功能集(例如硬件流控制或GPIO功能)的替代或自定义驱动程序。驱动文件下载:https://github.com/WCHSoftGroup/ch343s
- Spring Boot集成RabbitMQ的使用
码海浮生
后端Java技术类java-rabbitmqspringbootrabbitmq
作者:知识浅谈,CSDN签约讲师,CSDN博客专家,华为云云享专家,阿里云专家博主擅长领域:全栈工程师、爬虫、ACM算法微信:zsqtcyw联系我领取学习资料SpringBoot集成RabbitMQ的使用引言引入依赖配置RabbitMQ交换机、队列和绑定声明交换机和队列发送消息接收消息消息类型消息确认发送确认消费确认消息序列化监控与管理注意事项总结引言RabbitMQ是一个开源的消息代理和队列服务
- ACM题目和培养训练!!!
wretchedme
算法codecacm
ACM大量习题题库ACM大量习题题库现在网上有许多题库,大多是可以在线评测,所以叫做OnlineJudge。除了USACO是为IOI准备外,其余几乎全部是大学的ACM竞赛题库。USACOhttp://ace.delos.com/usacogate美国著名在线题库,专门为信息学竞赛选手准备TJUhttp://acm.tongji.edu.cn/同济大学在线题库,唯一的中文题库,适合NOIP选手ZJU
- 【node】Mac m1 安装nvm 和node
夜雨hiyeyu.com
vuemacoschrome前端vuevue.jsnvmjava
Macm1安装nvm和node一、使用brew安装nvm安装brewhome二、建立.nvm文件夹三、~/.zshrc或~/.bash_profile中配置如下四、nvm常用命令一、使用brew安装nvm安装brewhome安装国内版本/bin/bash-c"$(curl-fsSLhttps://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)
- 2012 - 正方形矩阵
寒燕舞
算法数据结构
题目描述晶晶同学非常喜欢方形,她希望打印出来的字符串也是方形的。老师给了晶晶同学一个字符串"ACM",晶晶同学突发奇想,如果任意给定义一个整数n,能不能打印出由这个字符串组成的正方形字符串呢?要求是每行要使用n个给定的字符串。请你编程实现一下。输入输入的第一行是一个正整数N(Nusingnamespacestd;intmain(){intn,m;cin>>n;for(intx=0;x>m;for(
- 【Tools】Mac brew工具
CodeWithMe
Toolsmacos
Homebrew(简称brew)是macOS(也支持Linux)上的一款包管理工具,它的作用类似于:Ubuntu下的aptCentOS下的yumArchLinux下的pacman一句话概括:brew是用来在macOS上安装、管理软件包的命令行工具。brew能做什么?安装CLI工具(如wget,git,cmake,python,node,ffmpeg等)安装GUI应用(如VisualStudioCo
- jxnu acm新生选拔赛
weixin_30474613
c/c++
最小的数ProblemDescription定义一种正整数集合K,集合中有N个数,集合中元素Ki(12#include3#include4#include5#include6#definelllonglong7usingnamespacestd;8constintMAX=1e4+10;9constintMOD=1e9+7;10intvis[10010],b[MAX*10],k;11voidinit
- [论文阅读] 人工智能+软件工程 | 用大语言模型架起软件需求形式化的桥梁
张较瘦_
前沿技术人工智能论文阅读软件工程
用大语言模型架起软件需求形式化的桥梁:一篇ACM调查草案的深度解读论文信息arXiv:2506.14627ACMSurveyDraftonFormalisingSoftwareRequirementswithLargeLanguageModelsArshadBeg,DiarmuidO’Donoghue,RosemaryMonahanComments:22pages.6summarytablesSu
- C++基础练习-二维数组
s15335
C++练习题c++开发语言
题目:https://acm.hdu.edu.cn/showproblem.php?pid=2022题解:#includeusingnamespacestd;intz[10000][10000];intmain(){intm,n;while(cin>>m>>n){intx,max=-1,l,c;//往数组里添加数据for(inti=0;i>z[i][j];}}//遍历数组并找出最大值for(int
- 数据结构-顺序表-数值统计
题目:https://acm.hdu.edu.cn/showproblem.php?pid=2008解答:#includeusingnamespacestd;#defineSLDataTypedoublestructSequlist{SLDataType*array;intsize;intcapacity;};//********************顺序表初始化***********/void
- scala的option和some
矮蛋蛋
编程scala
原文地址:
http://blog.sina.com.cn/s/blog_68af3f090100qkt8.html
对于学习 Scala 的 Java™ 开发人员来说,对象是一个比较自然、简单的入口点。在 本系列 前几期文章中,我介绍了 Scala 中一些面向对象的编程方法,这些方法实际上与 Java 编程的区别不是很大。我还向您展示了 Scala 如何重新应用传统的面向对象概念,找到其缺点
- NullPointerException
Cb123456
androidBaseAdapter
java.lang.NullPointerException: Attempt to invoke virtual method 'int android.view.View.getImportantForAccessibility()' on a null object reference
出现以上异常.然后就在baidu上
- PHP使用文件和目录
天子之骄
php文件和目录读取和写入php验证文件php锁定文件
PHP使用文件和目录
1.使用include()包含文件
(1):使用include()从一个被包含文档返回一个值
(2):在控制结构中使用include()
include_once()函数需要一个包含文件的路径,此外,第一次调用它的情况和include()一样,如果在脚本执行中再次对同一个文件调用,那么这个文件不会再次包含。
在php.ini文件中设置
- SQL SELECT DISTINCT 语句
何必如此
sql
SELECT DISTINCT 语句用于返回唯一不同的值。
SQL SELECT DISTINCT 语句
在表中,一个列可能会包含多个重复值,有时您也许希望仅仅列出不同(distinct)的值。
DISTINCT 关键词用于返回唯一不同的值。
SQL SELECT DISTINCT 语法
SELECT DISTINCT column_name,column_name
F
- java冒泡排序
3213213333332132
java冒泡排序
package com.algorithm;
/**
* @Description 冒泡
* @author FuJianyong
* 2015-1-22上午09:58:39
*/
public class MaoPao {
public static void main(String[] args) {
int[] mao = {17,50,26,18,9,10
- struts2.18 +json,struts2-json-plugin-2.1.8.1.jar配置及问题!
7454103
DAOspringAjaxjsonqq
struts2.18 出来有段时间了! (貌似是 稳定版)
闲时研究下下! 貌似 sruts2 搭配 json 做 ajax 很吃香!
实践了下下! 不当之处请绕过! 呵呵
网上一大堆 struts2+json 不过大多的json 插件 都是 jsonplugin.34.jar
strut
- struts2 数据标签说明
darkranger
jspbeanstrutsservletScheme
数据标签主要用于提供各种数据访问相关的功能,包括显示一个Action里的属性,以及生成国际化输出等功能
数据标签主要包括:
action :该标签用于在JSP页面中直接调用一个Action,通过指定executeResult参数,还可将该Action的处理结果包含到本页面来。
bean :该标签用于创建一个javabean实例。如果指定了id属性,则可以将创建的javabean实例放入Sta
- 链表.简单的链表节点构建
aijuans
编程技巧
/*编程环境WIN-TC*/ #include "stdio.h" #include "conio.h"
#define NODE(name, key_word, help) \ Node name[1]={{NULL, NULL, NULL, key_word, help}}
typedef struct node { &nbs
- tomcat下jndi的三种配置方式
avords
tomcat
jndi(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。命名服务将名称和对象联系起来,使得我们可以用名称
访问对象。目录服务是一种命名服务,在这种服务里,对象不但有名称,还有属性。
tomcat配置
- 关于敏捷的一些想法
houxinyou
敏捷
从网上看到这样一句话:“敏捷开发的最重要目标就是:满足用户多变的需求,说白了就是最大程度的让客户满意。”
感觉表达的不太清楚。
感觉容易被人误解的地方主要在“用户多变的需求”上。
第一种多变,实际上就是没有从根本上了解了用户的需求。用户的需求实际是稳定的,只是比较多,也比较混乱,用户一般只能了解自己的那一小部分,所以没有用户能清楚的表达出整体需求。而由于各种条件的,用户表达自己那一部分时也有
- 富养还是穷养,决定孩子的一生
bijian1013
教育人生
是什么决定孩子未来物质能否丰盛?为什么说寒门很难出贵子,三代才能出贵族?真的是父母必须有钱,才能大概率保证孩子未来富有吗?-----作者:@李雪爱与自由
事实并非由物质决定,而是由心灵决定。一朋友富有而且修养气质很好,兄弟姐妹也都如此。她的童年时代,物质上大家都很贫乏,但妈妈总是保持生活中的美感,时不时给孩子们带回一些美好小玩意,从来不对孩子传递生活艰辛、金钱来之不易、要懂得珍惜
- oracle 日期时间格式转化
征客丶
oracle
oracle 系统时间有 SYSDATE 与 SYSTIMESTAMP;
SYSDATE:不支持毫秒,取的是系统时间;
SYSTIMESTAMP:支持毫秒,日期,时间是给时区转换的,秒和毫秒是取的系统的。
日期转字符窜:
一、不取毫秒:
TO_CHAR(SYSDATE, 'YYYY-MM-DD HH24:MI:SS')
简要说明,
YYYY 年
MM 月
- 【Scala六】分析Spark源代码总结的Scala语法四
bit1129
scala
1. apply语法
FileShuffleBlockManager中定义的类ShuffleFileGroup,定义:
private class ShuffleFileGroup(val shuffleId: Int, val fileId: Int, val files: Array[File]) {
...
def apply(bucketId
- Erlang中有意思的bug
bookjovi
erlang
代码中常有一些很搞笑的bug,如下面的一行代码被调用两次(Erlang beam)
commit f667e4a47b07b07ed035073b94d699ff5fe0ba9b
Author: Jovi Zhang <
[email protected]>
Date: Fri Dec 2 16:19:22 2011 +0100
erts:
- 移位打印10进制数转16进制-2008-08-18
ljy325
java基础
/**
* Description 移位打印10进制的16进制形式
* Creation Date 15-08-2008 9:00
* @author 卢俊宇
* @version 1.0
*
*/
public class PrintHex {
// 备选字符
static final char di
- 读《研磨设计模式》-代码笔记-组合模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
abstract class Component {
public abstract void printStruct(Str
- 利用cmd命令将.class文件打包成jar
chenyu19891124
cmdjar
cmd命令打jar是如下实现:
在运行里输入cmd,利用cmd命令进入到本地的工作盘符。(如我的是D盘下的文件有此路径 D:\workspace\prpall\WEB-INF\classes)
现在是想把D:\workspace\prpall\WEB-INF\classes路径下所有的文件打包成prpall.jar。然后继续如下操作:
cd D: 回车
cd workspace/prpal
- [原创]JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
comsci
eclipse设计模式算法工作swing
JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
&nb
- SecureCRT右键粘贴的设置
daizj
secureCRT右键粘贴
一般都习惯鼠标右键自动粘贴的功能,对于SecureCRT6.7.5 ,这个功能也已经是默认配置了。
老版本的SecureCRT其实也有这个功能,只是不是默认设置,很多人不知道罢了。
菜单:
Options->Global Options ...->Terminal
右边有个Mouse的选项块。
Copy on Select
Paste on Right/Middle
- Linux 软链接和硬链接
dongwei_6688
linux
1.Linux链接概念Linux链接分两种,一种被称为硬链接(Hard Link),另一种被称为符号链接(Symbolic Link)。默认情况下,ln命令产生硬链接。
【硬连接】硬连接指通过索引节点来进行连接。在Linux的文件系统中,保存在磁盘分区中的文件不管是什么类型都给它分配一个编号,称为索引节点号(Inode Index)。在Linux中,多个文件名指向同一索引节点是存在的。一般这种连
- DIV底部自适应
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- Centos6.5使用yum安装mysql——快速上手必备
dcj3sjt126com
mysql
第1步、yum安装mysql
[root@stonex ~]# yum -y install mysql-server
安装结果:
Installed:
mysql-server.x86_64 0:5.1.73-3.el6_5 &nb
- 如何调试JDK源码
frank1234
jdk
相信各位小伙伴们跟我一样,想通过JDK源码来学习Java,比如collections包,java.util.concurrent包。
可惜的是sun提供的jdk并不能查看运行中的局部变量,需要重新编译一下rt.jar。
下面是编译jdk的具体步骤:
1.把C:\java\jdk1.6.0_26\sr
- Maximal Rectangle
hcx2013
max
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
public class Solution {
public int maximalRectangle(char[][] matrix)
- Spring MVC测试框架详解——服务端测试
jinnianshilongnian
spring mvc test
随着RESTful Web Service的流行,测试对外的Service是否满足期望也变的必要的。从Spring 3.2开始Spring了Spring Web测试框架,如果版本低于3.2,请使用spring-test-mvc项目(合并到spring3.2中了)。
Spring MVC测试框架提供了对服务器端和客户端(基于RestTemplate的客户端)提供了支持。
&nbs
- Linux64位操作系统(CentOS6.6)上如何编译hadoop2.4.0
liyong0802
hadoop
一、准备编译软件
1.在官网下载jdk1.7、maven3.2.1、ant1.9.4,解压设置好环境变量就可以用。
环境变量设置如下:
(1)执行vim /etc/profile
(2)在文件尾部加入:
export JAVA_HOME=/home/spark/jdk1.7
export MAVEN_HOME=/ho
- StatusBar 字体白色
pangyulei
status
[[UIApplication sharedApplication] setStatusBarStyle:UIStatusBarStyleLightContent];
/*you'll also need to set UIViewControllerBasedStatusBarAppearance to NO in the plist file if you use this method
- 如何分析Java虚拟机死锁
sesame
javathreadoracle虚拟机jdbc
英文资料:
Thread Dump and Concurrency Locks
Thread dumps are very useful for diagnosing synchronization related problems such as deadlocks on object monitors. Ctrl-\ on Solaris/Linux or Ctrl-B
- 位运算简介及实用技巧(一):基础篇
tw_wangzhengquan
位运算
http://www.matrix67.com/blog/archives/263
去年年底写的关于位运算的日志是这个Blog里少数大受欢迎的文章之一,很多人都希望我能不断完善那篇文章。后来我看到了不少其它的资料,学习到了更多关于位运算的知识,有了重新整理位运算技巧的想法。从今天起我就开始写这一系列位运算讲解文章,与其说是原来那篇文章的follow-up,不如说是一个r
- jsearch的索引文件结构
yangshangchuan
搜索引擎jsearch全文检索信息检索word分词
jsearch是一个高性能的全文检索工具包,基于倒排索引,基于java8,类似于lucene,但更轻量级。
jsearch的索引文件结构定义如下:
1、一个词的索引由=分割的三部分组成: 第一部分是词 第二部分是这个词在多少