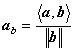向量、矩阵乘法的几何意义(一) scalar multiplication VS scalar product
1、scalar multiplication 纯量乘法
(1)定义:
纯量乘法是指一个标量r与一个向量V(或矩阵M)相乘,其结果为一个向量(矩阵),该向量(矩阵)的每一个元素为标量r与V(M)中对应位置元素的乘积。
(2)几何意义:
Scaling:对向量(矩阵)各维上的伸(stretch, r>1)缩(shrink, 0<r<1)。Scalar multiplication is a way to change the size of a configuration of points by stretching or shrinking them on all dimensions.
2、scalar product (dot product, inner product) 数积、标量积、内积
(1) 定义:两个向量的内积的结果是一个标量,其定义如下
(1)
(2)
(2) 几何意义:
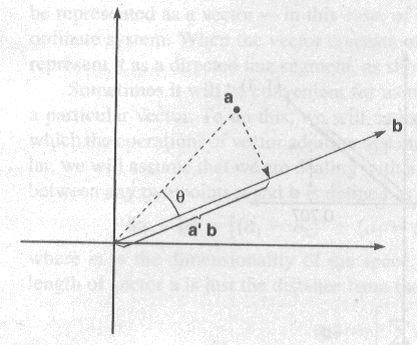
Projection:如图1所示,两个向量的内积可以看做是其中一个向量(看成向量空间中的一个点)向另一个向量(看成向量空间中的一条有向线段,directed line segment)的投影,投影的距离长度为内积的值。
还有一种说法是向量a在向量b上的投影是
图1 两向量内积的几何解释
参考资料:
《Analyzing Multivariate Data》
http://en.wikipedia.org/wiki/Scalar_multiplication
http://www.purplemath.com/modules/mtrxmult.htm