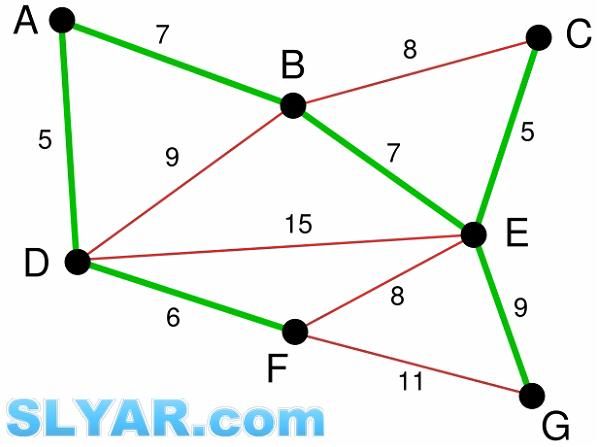
最小生成树实现(kruskal+并查集)续
题目:(和上篇的那个题目差不多,不过里用到了路径压缩,所以效率更高。还有就是数据后面输入的,所以,更上篇的那个题目还是有区别。)
输入数据:
具体实现代码(C++):
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 100
//定义边(x,y),权值为W
typedef struct
{
int x,y;
int w;
}edge;
edge e[MAX];
//rank[x]表示x所在树的高度
int rank[MAX];
// father[x]表示x的父节点
int father[MAX];
int sum;
//比较函数,按权值(相同则按x坐标)非降序排序
int cmp(const void *a,const void *b)
{
if((*(edge *)a).w == (*(edge *)b).w)
{
return (*(edge *)a).x - (*(edge *)b).x;
}
return (*(edge *)a).w - (*(edge *)b).w;
}
//初始化集合
void Make_Set(int x)
{
father[x] = x;
rank[x] = 1;
}
//查找x元素所在的集合,回溯是压缩路径
int Find_Set(int x)
{
if(x != father[x])
{
father[x] = Find_Set(father[x]);//递归压缩
}
return father[x];
}
//合并x,y所在的集合
void Union(int x,int y,int w)
{
if(x == y) return;
//将高度较小的连接在高度较大的树后
if(rank[x] == rank[y]){
rank[x] = rank[y] + 1;
father[y] = x;
}else if(rank[x] < rank[y])
father[x] = y;
else
father[y] = x;
sum += w;
}
//主函数
int main()
{
int i,n;
int x,y;
char chx,chy;
//读取边的数目
cin>>n;
//读取边信息并初始化集合
for(i = 0; i < n; i++)
{
cin>>chx>>chy>>e[i].w;
e[i].x = chx - 'A';
e[i].y = chy - 'A';
Make_Set(i);
}
//将边排序
qsort(e,n,sizeof(edge),cmp);
sum = 0;
for(i = 0; i < n; i++)
{
x = Find_Set(e[i].x);
y = Find_Set(e[i].y);
if(x != y)
{
printf("%c - %c:%d\n",e[i].x + 'A',e[i].y + 'A',e[i].w);
Union(x,y,e[i].w);
}
}
printf("MST Total:%d\n",sum);
return 0;
}
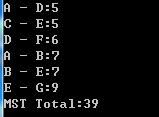
运行结果: