基于GML的几何数据模型
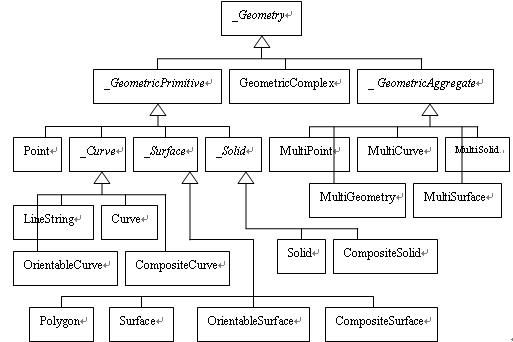
目前GML 3.1.0版本中所使用的几何模型的XML模式文档包括: geometryBasic0d1d.xsd、geometryBasic2d.xsd、geometryPrimitives.xsd、geometryAggregates.xsd、geometryComplexes.xsd。其中,geometryBasic0d1d.xsd 的部分类型和元素是为了兼容以前的GML2版本(GML2中只有一个模式geometry.xsd),其它的几个模式文档则完全是由新的类型和元素组成的。下图是GML中几何模型的类型层次。
其中,_Geometry元素是所有GML3几何元素的置换组的抽象头(head)元素,这包括预定义的和用户自定义的几何元素。任何几何元素必须是抽象几何类型(AbstractGeometryType)的直接或间接的扩充或限制,同时必须直接或间接属于_Geometry置换组。
从图中可以看出,几何模型分为基本几何(geometric primitives)、聚合几何(aggregates)和复杂几何(complexes)。
基本几何(也就是AbstractGeometricPrimitiveType的子类型的实例)可被打开,就是说它们不包含边界点。曲线(curves)不包含终点,面(surfaces)不包含边界曲线,体(solids)不包含边界面。
聚合几何(也就是AbstractGeometricAggregateType的子类型的实例),是几何元素的任意聚合。它们被假定为没有任何附加的内部结构,是许多指定类型的几何的聚合。应用模式可按自己的表达方式为需要多个几何对象描述的要素使用聚合。
复杂几何(即GeometricComplexType的实例)是基本几何的闭集,即它们包含边界。
下面就以基本几何中的二维图元Polygon为例说明一下在GML中如何表示地理特征。在GML中定义的Polygon的Schema为:
<complexType name="PolygonType">
<complexContent>
<extension base="gml:AbstractSurfaceType">
<sequence>
<element ref="gml:exterior" minOccurs="0" />
<element ref="gml:interior" minOccurs="0"
maxOccurs="unbounded" />
</sequence>
</extension>
</complexContent>
</complexType>
<element name="Polygon" type="gml:PolygonType"
substitutionGroup="gml:_Surface" />
Polygon是一个多边形的曲面,元素exterior和interior分别描述了多边形的曲面的内外边界,他们的定义如下:
<element name="exterior" type="gml:AbstractRingPropertyType" />
一个由许多环组成的曲面的边界。在标准的2维情况下,这些环中的一个作为外部边界区别于其它环。在通常的多种情况下,所有的边界都作为内部边界列出来且外部边界为空不总是可能的。
<element name="interior" type="gml:AbstractRingPropertyType" />
一个由许多环组成的曲面的边界。“interior”环将曲面或者曲面片从由环闭合形成的区域中分开。gml:AbstractRingPropertyType封装一个环来表示曲面的曲面边界特性。