栈和队列（二）：栈的应用举例

一、数制转换

　　十进制数N和其它d进制数的转换是计算机实现计算的基本问题，其解决方法很多，其中一个简单的算法是基于下列原理：
　　　　　　N = (N div d) * d + N mod d。其中：div为整除运算，mod为求余运算。
　　　　例：(1348)₁₀ = (2504)₈，其运算过程如下：
　　　　　　    N　　　　N div 8　　　　N mod 8
　　　　　　1348　　　　168　　　　　　  4
　　　　　　  168　　　　  21  　　           0
　　　　　　    21 　　        2　　　　　　  5
　　　　　　　　2　　         0　　 　　       2 　

 　　　　从上述运算过程可见：①从低位到高位顺序产生八进制数的各个位数；②与打印输出由高位到低位的顺序相反。

　　因此，将计算过程中得到的八进制数的各位顺序进栈，再按出栈序列打印输出，即可得到与输入对应的八进制数。

 

二、括号匹配的检验 

　　假设表达式中允许包含两种括号：圆括号和方括号，其嵌套的顺序随意，即([]())或[([][])]等均为正确的格式，[(])或([())均为不正确的格式。

　　检验括号是否匹配的方法：运用“期待的急迫程度”的概念。

　　　　例：考虑下列括号序列

　　　　　　[　　(　　[　　]　　[　　]　　)　　]

　　　　　　1　　2　 3　  4　　5　  6　  7     8

　　　　分析：1.计算机接受第1个括号后，期待与之匹配的第8个括号出现。
　　　　　　　2.获得第2个括号，此时第1个括号暂时放在一边，而急迫期待与之匹配的第7个括号出现。

　　　　　　   3.获取第3个括号，此时又把第2个括号暂时放在一边，而急迫期待与之匹配的第4个括号出现，第3个括号的期待得到满足，消解之后，第2个括号的期待匹配又成为当前最急迫的任务了。

　　　　　　   4.以此类推，可见，该处理过程与栈的特点吻合。

　　　　算法的思路：1.设置一个栈，顺序读入括号。

　　　　　　　　　　2.若是右括号，则或者使置于栈顶的最急迫期待得以消解，或则是不合法的情况。

　　　　　　　　　　3.若是左括号，则作为一个新的最急迫的期待压入栈中，自然使原有在栈中所有未消解的期待的急迫性降了一级。

　　　　　　　　　　说明：在此算法的开始和结束时，栈都应该是空的。

 

三、迷宫求解 

　　计算机解迷宫的方法：“穷举求解”法，即从入口出发，顺某一方向向前探索，若能走通，则继续网前走，否则沿原路退回，换一个方向再继续探索，直到所有的通路都探索到为止。如下图为一迷宫

　　　　　　　　　　

　　　　　　求一条路径算法的基本思想：假设以栈S记录当前路径，则栈顶中存放的是“当前路径上最后一个通道块”：

　　　　　　1.若当前路径可通，则纳入“当前路径”——当前位置入栈操作，并继续朝下一个位置“探索”，即切换下一位置为当前位置，如此重复直至到达出口。

　　　　　　2.若当前位置不可通，则应该顺着“来向”退回到前一通道块，然后朝着除来向之外的其他方向继续探索。

　　　　　　3.若该通道的4个方向均不可通，则应该从“当前路径”上删除该通道块——出栈操作。 

  

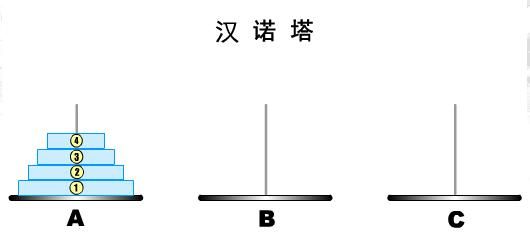
四、Hanoi塔问题 

　　n阶Hanoi塔问题。假设有3个分别命名为X,Y,Z的塔座，在塔座X上插有n个直径大小不同、依小到大编号为1，2，……，n的圆盘，如下图。现要求将X轴上的n个圆盘移到Z上并仍按同样的顺序叠排，圆座移动必须遵循下列规则：

　　(1)每次只能移动一个圆盘。

　　(2)圆盘可以插在X,Y,Z中的任一塔座上。

　　(3)任何时刻都不能将一个教大的圆盘压在较小的圆盘之上。

　　　　

　　解决方法：

　　当n = 1时，直接把圆盘从X移到Z。

　　当n > 1时，先把上面的n-1个圆盘从X移到Y，然后将n号盘从X移到Z，再将n-1个盘从Y移到Z。

　　即把求解n个圆盘的Hanoi问题转化为求解n-1 个圆盘的Hanoi问题，依次类推，直到转化成只有一个圆盘的Hanoi问题。

　　执行情况：递归工作栈保存内容：形参n，x，y，z。代码如下

代码

     void  Move( char  x,  char  y)
    {
        Console.Write( string .Format( " {0}-->{1} " , x, y));
        Console.WriteLine();
    }
     void  Hanoi( int  n,  char  one,  char  two,  char  three)
    {
         if  (n  ==   1 ) 
            Move(one, three);
         else
        {
            Hanoi(n  -   1 , one, three, two);
            Move(one, three);
            Hanoi(n  -   1 , two, one, three);
        }
    }

 注：该算法通过递归实现，栈在递归算法的内部中所起到的什么样的作用呢？

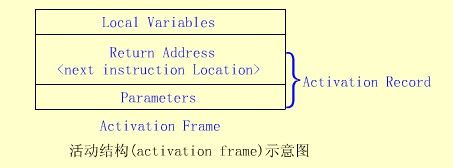
　　①调用函数时：系统将会为调用者构造一个由参数表和返回地址组成的活动记录，并将其压入到由系统提供的运行时刻栈的栈顶，然后将程序的控制权转移到被调函数。若被调函数有局部变量，则在运行时刻栈的栈顶也要为其分配相应的空间。因此，活动记录和这些局部变量形成了一个可供被调函数使用的活动结构。 

　　

　　　　注意：参数表的内容为实参，返回地址是函数调用语句的下一指令的位置。
　　②被调函数执行完毕时：系统将运行时刻栈栈顶的活动结构退栈，并根据退栈的活动结构中所保存的返回地址将程序的控制权转移给调用者继续执行。