平衡边界作业算法并发仿真测试网络存储系统的响应时间
传送门 ☞ Android兵器谱 ☞ 转载请注明 ☞ http://blog.csdn.net/leverage_1229
一、实验参数列表
二、MATLAB脚本(balanced job bounds.m)
clear;
N = input('SAN Performance N = ');
L = input('Queue length L = ');
Z = input('Thinking time Z = ');
%testing a group of data
% N = 60;
% L = 32;
% Z = 0.24;
%model M/M/1
%host
E1 = 1/(64*33/8)+0.0002;
for n = 1 : L
u(n) = (sqrt(n*n+4*n)-n)/2; %utilization in percent
rate(1,n) = u(n)/E1; %I/O request rate in IOPS
arate1 = sum(rate(1,n))/n;
end
D(1) = E1 + arate1*(E1^2)/(2*(1-arate1*E1));
%fcf
E2 = 1/1062.5;
for n = 1 : L
arate2 = rate(1,n);
D(2) = arate2*(E2^2)/(2*(1-arate2*E2));
end
%dacc
h = 2.283;
v = 2.798;
E3 = 1/(64*66/8)+0.00016;
% E3 = 1/(64*66/8)+0.00018;
ts = E3+(E3^2)*sqrt(1.39794);
for n = 1 : L
u(n) = (sqrt(n*n+4*n)-n)/2; %utilization in percent
rate(3,n) = u(n)/E3; %I/O request rate in IOPS by read
% rate(3,n) = u(n)/E3; %I/O request rate in IOPS by write
arate3 = sum(rate(3,n))/n;
% arate3 = sum(rate(3,n))/n;
D(3) = ts+((0.5*(h+(4*v-3*h-1)*0.5)+2*(1+h-2*v)*0.25)*(1/(E3^2))*arate3*E3*(2*(E3^2)))/((1/E3)-arate3);
% D(3) = ts+((0.5*(h+(4*v-3*h-1)*0.5)+2*(1+h-2*v)*0.25)*(1/(E3^2))*arate3*E3*(2*(E3^2)))/((1/E3)-arate3);
end
%disk
E4 = 2*(0.05/30+(1-0)*(8.9+4.16)*0.05/1)*10^-3;
% E4 = (0.6+0.0876*sqrt(14100)+(1/10025)*60*1000/2+0.8+0.2+1.2)*10^-3;
% E4 = (0.9+0.0910*sqrt(14100)+(1/10025)*60*1000/2+0.8+0.2+1.2)*10^-3;
for n = 1 : L
u(n) = (sqrt(n*n+4*n)-n)/2; %utilization in percent
rate(4,n) = u(n)/E4; %I/O request rate in IOPS
arate4 = sum(rate(4,n))/n;
end
D(4) = E4 + arate4*(E4^2)/(2*(1-arate4*E4));
Dmax = max(D(1:4)); % maximum service demand per code
Dsum = D(1)+D(2)+D(3)+D(4); % sum of total service demands
Davg = Dsum/4; % average service demand per queue
for n = 1:N
Rmin(n) = max(n * Dmax - Z, Dsum + ((n-1)*Davg*Dsum/(Dsum+Z))); % lower bound of response time
Rmax(n) = Dsum + ((n-1)*Dmax*(n-1)*Dsum/(((n-1)*Dsum)+Z)); % upper bound of response time
end
% response time of MVA
for m = 2:4
L(m) = 0;
end
for n = 1:N
R(1) = D(1);
for m = 2:4
R(m) = D(m) * (1 + L(m));
end
Tau = n / sum(R(:));
for m = 2:4
L(m) = Tau * R(m);
end
Rn(n,1) = D(1);
for m = 2:4
Ln(n,m) = L(m);
Rn(n,m) = R(m);
end
Taun(n) = Tau;
end
for n = 1:N
RTn(n) = sum(Rn(n,2:4)); % average response time
end
t = 1:N;
% response time
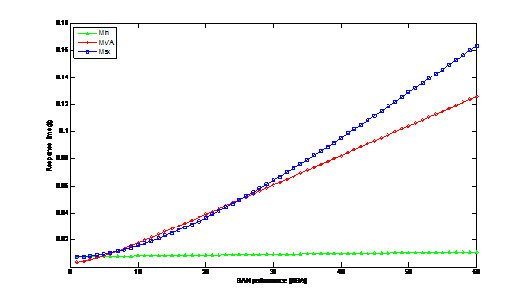
figure(1), plot(t, Rmin, 'g', t, RTn, 'r', t, Rmax, 'b'),xlabel('SAN performance (MB/s)'),ylabel('Response time(s)');
三、NSS(网络存储系统)边界性能