【编程珠玑】空间换时间的数据结构问题

One problem with trading more space to use less time is that initializing the space can itself take a great deal of time. Show how to circumvent this problem by designing a technique to initialize an entry of a vector to zero the first time it is accessed. Your scheme should use constant time for initialization and for each vector access, and use extra space proportional to the size of the vector. Because this method reduces initialization time by using even more space, it should be considered only when space is cheap, time is dear and the vector is sparse.[译]使用更多的空间来换取更少的运行时间存在一个问题：初始化空间本身需要消耗大量的时间。说明如何设计一种技术，在第一次访问向量的项时将其初始化为0。你的方案应该使用常量时间进行初始化和向量访问，使用的额外空间应正比于向量的大小。因为该方法通过进一步增加空间来减少初始化的时间，所以仅在空间很廉价、时间很宝贵且向量很稀疏的情况下才考虑使用。（来源于《编程珠玑》第2版的第1章中第8页习题9）

分析

首先，我们应该对题目进行彻底分析---我们需要访问的是一个长度(假设为n)非常大的数组，一般而言对数组中某个元素访问前我们必须要进行初始化，但是当n值非常大而程序对time要求较严格时，对所有的数组元素都进行统一的初始化是不可取的。为了达到程序对time的要求，我们应该对需要访问的元素(它的个数相对于n来说很小)进行初始化。

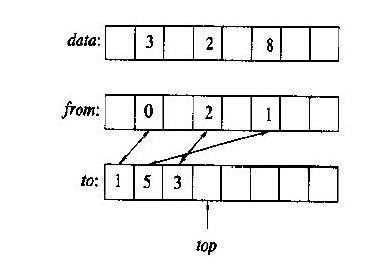
其次，对元素初始化的判断---为了提高判断的准确性，答案引入了两个数组from和to以及整数top，且对于元素data[i]已初始化的条件是from[i]<top && to[from[i]]==i。现在让我们来具体分析这些规则是如何被应用的：假设当我们第一次访问的数组元素下标为1时，先判断初始化条件(此时数组from和to都没有初始化，当然time也不允许让我们多管闲事)，一般而言from[1]中的随机数是大于top(现在为0)的，但我们不能保证，于是我们加入了第二个判断条件--to[from[1]]==1,对于这个表达式我们两次取随机值且让后者等于1，这样的概率有但几乎为0！因此，data[1]未被初始化，于是执行from[1]=top; to[top]=1; data[1]=0; top++；这样做的目的就是保证以后再次访问data[1]时不需要再初始化(条件满足了直接读取即可)。

最后，对于该方法的可靠性分析---让我们先来分析一下整数top的作用，不难发现，top记录了当前data中已初始化元素的个数，但主要是保证了from中已初始化的元素都小于top(通过from[i]=top; top++)，这给我们的判断条件(from[i]<top)提供了一定的可靠性，当然再加上第二到保险(to[from[i]]==i)使得此方法可靠性值得信赖!

解答

（来自于《编程珠玑》第2版部分习题答案）

借助于两个额外的n元向量from、to和一个整数top,我们就可以使用标识来初始化向量data[0....n-1]。如果元素data[i]已始化，那么from[i] < top并且 to[from[i]] =i.因此，from是一个简单的标识，to和top一起确保了from中不会被写入内存里的随机内容。下图中data的空白项未被始化：

变量top初始为0,下面的代码实现对数组元素i首次访问：

from[i] =top;
to[top] = i;
data[i] = 0;
top ++;

总结

这个以空间换时间的数据结构是很Amusing的。首先应考虑初始化数组导致的直接结果是什么？ 就是第一次访问某个元素的时候，这个元素的值是初始化后的值。由此就想到了，我们提出的算法应该能够实现：当我们第一次访问某个元素的时候，这个元素的值是初始化后的值。这个实现的关键点是：如何判断是第一次访问，即如何判断数组中的元素是初始化过还是没有初始化过。思考如下几点：

1）当时我看这道题的时候第一个反应就是：再建立一个数组，然后第一次访问时候将已初始化元素的数组下标存储在里面，每次访问的时候查询这个数组，要是数组下标在里面，就说明这个数组下标的元素已经被初始化了。相信很多人都有同样的想法，但是如果这样做的话，虽然节省了初始化的时间，但是每次访问都要在存已访问元素下标的数组里进行线性搜索，这样的时间也是浪费不少，如何不用线性时间而用常数时间就能判断是否一个数组元素是否初始化过呢？？

2）然后我就又想到，还不如建立一个和需要访问数组等长的数组，在访问某个元素的时候先看这个数组，要是这个数组的对应元素标记为1则表示已经初始化过了，没有就把相应元素置为1。不过同样 ，这个等长的数组没有被初始化过，那么它里面存储的随机数有很大的概率就是1，这样很容易误判。

3）然后我看了习题答案后，恍然大悟。作者通过巧妙地利用from和to数组以及整数top保障了方法的可靠性~~~

=========================================================================================

转载请注明出处：http://blog.csdn.net/utimes/article/details/8760313