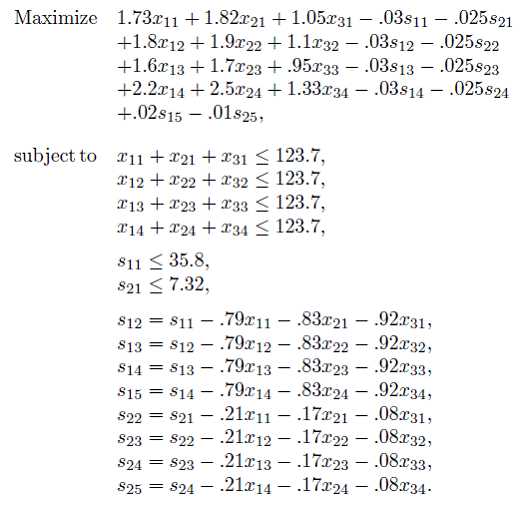AMPL：A Mathematical Programming Language 翻译

    最近翻译了一篇有关AMPL作者写的文章，点击下载(把下载后的文件扩展名改为rar然后解压即可)，后面附录的例子见这里。

AMPL：一门数学规划语言

Robert Fourer

西北大学，Evanston，伊利诺伊州，60201

Brian W. Kernighan

贝尔实验室，Murray Hill，新泽西州，07974

Robert Fourer, David M. Gay and Brian W. Kernighan. A Modeling Language for Mathematical Programming. Management Science 36 (1990) 519-554

摘 要

    实践中的大规模数学规划不只是牵涉到一个算法来最小或最大化一个目标函数。在我们调用任何优化程序之前，我们要花费相当的力气在刻画一个模型和产生适用于计算的数据安排。AMPL是让这些步骤更容易也更少犯错误的一门新语言，采用了非常类似于许多建模人员用于描述数学规划的符号代数标记，不过它是规范和形式的，足以能被计算机系统处理，它特别引人注目之处在于它的语法的一般性和多样的索引操作。我们已经实现了一个翻译器，它把一个线性规划模型及其相关数据做为输入，产生适合于标准线性规划求解器求解的输出。语言和翻译器可以直接地被扩展到能够处理包含非线性表达和离散变量的更一般的数学规划问题。

1. 引言

    实践中的大规模数学规划问题不只是牵涉到一个算法来进行优化。在任何优化算法使用之前，我们必须花费相当的力气来刻画潜在的模型并产生必要的数据模式。

    如果算法能够处理就像人们能做的那样形式的优化问题，那么模型的公式化和产生阶段的任务就相对的容易了。然而，实际上建模人员能够明晰的问题的形式和算法能够求解的形式存在许多的不同。从“建模者形式”到“算法形式”的可靠转换经常是相当的费时费力。

   传统的做法是把工作在人和计算机之间进行分配。首先，我们写一个计算机程序把建模人员能够理解的形式转化成需要的数据形式。然后，计算机编译和执行这个程序来创建一个算法形式。这种做法经常费时费力并且易于出错，最为严重的是程序必须由建模人员调试，而它的输出也就是算法形式人读起来往往很困难。

    在重要的特例线性规划中，大多数算法形式都是约束系数矩阵表示。典型的情况是矩阵往往是稀疏的，它有成百上千的行和列，非零元素的分布也是错综复杂的。产生紧凑的系数表示的程序就是所谓的矩阵产生器。几门编程语言被设计专门用来针对矩阵产生器(Haverly Systems 1977, Creegan 1985)，标准语言蔽日Fortran也经常被使用(Beale 1970)。

   在建模者形式到算法形式的翻译中的许多困难都可以通过使用针对数学规划的建模语言得到回避。这种建模语言被设计成把建模者形式表示为计算机系统能够直接理解的输入。这样算法形式的翻译完全由计算机执行，而省去了中间的编程步骤。建模语言相比于矩阵产生器的优点Fourer有详尽的分析（1983）。诸如GAMS (Bisschop and Meeraus 1982; Brooke, Kendrick and Meeraus 1988)和MGG(Simons 1987)的实现始于20世纪70年代，最近几年加快了开发的速度。

    在本文中我们描述了AMPL语言的设计和实现。同以前的语言相比，AMPL最为突出的是它的语法的一般性，和在建模者形式中经常使用的代数符号的相似性。针对索引集合的定义和一系列的逻辑表达式，AMPL提供了不同的类型和操作。AMPL从XML原型语言（Fourer 1983）获取了相当多的灵感，不过也包含了诸多的改变和扩展。

    AMPL通过一个最大收益产品问题这样一个简单例子引入。第2、3和4节使用了更复杂的例子来检验语言设计方面的细节。我们试着简单设计语言最基本的特征，而避免一些特殊的细节，那应该是语言用户指南和参考手册包含的内容。我们重点是描绘特别重要或困难的语言的设计决定等方面。

   AMPL仅仅被单独用来描述几类数学规划模型。为了让它有用，还必须把它包含到一个系统中，由系统来管理数据、模型和解。第5节讨论一个针对AMPL模型的数据表示，第6节描述了我们的一个能够解释模型及其数据的实现。解释器的输出是一个能够适合绝大多数算法的数学规划的表示。对于大量含有超过一千个约束和一万个变量的实际问题的计时表明转化的计算费用相比于优化的费用是十分合理的。

    我们打算让AMPL能够表示许多种类的数学规划。然而限于本文的篇幅，我们仅限于讨论线性规划的问题和例子。第7节比较了AMPL与其它的线性规划使用的语言，也指出AMPL怎样扩展到其它种类的模型，怎样集成到其它的建模软件中。附录罗列了四个AMPL线性规划的例子，它们的一部分在正文中用做示例。

1.1 引例

    图1-1罗列了一个简单线性规划模型的代数表示，就像在普通报告或论文中的那样。整个表示从模型需要的索引集和数值参数的描述开始，接着定义了决策变量，最后目标函数和约束条件做为索引集、参数和变量的表达式而给出。

    在图1-1的代数表示并没有定义任何特定的问题。这样表示的目的是指定一类有着共同数据和目标的表示。如果我们想定义一个特定的问题，就必须为这个表示中的集和参数提供相应的数据。每个不同的集和数据的说明就产生一个不同的问题。为了区分通用表示和特定问题，我们称前者是模型称后者是线性规划或LP。

    在处理超大的线性优化问题时通用模型和特定线性规划问题之间的区别就是本质的。做为一个实例，图1-2a给出前面表示的小实例的一系列数据：2个原材料，3个最终产品和4个周期。在这样的一个小实例中，目标函数和约束条件容易显示列出来，见1-2b。假如现在我们有10个原材料，30个产品和20个周期。图1-1的模型不用改变，图1-2a的数据表仍然在两页之内；但是线性规划扩展到230个约束和810个变量，它的显示罗列显然太大而不利于阅读。如果周期数进一步扩展到40，模型不需要改变，仅仅一个数据表（期望利润）扩大为原来的两倍，尽管线性规划的变量数和约束数大致上都变为原来的两倍。

    我们将使用术语：模型翻译器来描述这样的计算机系统，它除了形如图1-2a的数据以外以图1-1的紧凑代数形式读入一个模型，再用形如图1-2b的繁琐形式写出相应的线性规划。对于实际的实现，数据输入能给出更多的机器可读的安排，显式输出能被写成更适合于一个高效算法的格式。然而翻译面临的主要障碍在于要设计一种语言，它能够清晰地表述一个紧凑的代数模型，并且它也能被一个计算机系统读取和解释。

    AMPL就是这样一种语言。图1-1模型的AMPL表示见图1-3，并用来在整个引言中来示例说明语言的特征。

    一个AMPL翻译器通过读、解析和解释形如图1-3的模型作为开始，然后读入一些特定数据的表示，图1-4就显示了针对图1-2a数据的合适的格式，接着模型和数据就被处理用以确定它们所表示的线性规划，最后线性规划就被写成一种合适的形式。

    当AMPL用这种方式被使用的时候，留给人们的主要工作就是模型的表示和数据的收集。此外，如果一个模型起初就被用传统代数符号表示的话，那么我们必须把它转换成AMPL能够使用的语句。然而AMPL设计成让这种转换更像转述而不是翻译。例如，在图1-3中的几乎所有的表达式都能从与图1-1中相似的表达式用一种直接的方式确定。

    因为AMPL要由计算机读取，所以它确实有几个明显的方面与代数符号不同。语法更规则，例如每个参数的生明以param起头，以分号结尾。像传统的数学符号像和都被用清晰的仅使用ASCII码的表达式所代替。AMPL语法允许多字符名，然而单字符名更为适合于传统的代数表达式。

    代数模型的五个主要部分—集、参数、变量、目标和约束—在AMP模型中也是五组成部分。本节的剩余部分简要介绍每个组成部分及其AMPL表示。在最后我们也评论一下数据格式。

给定参数：

    一个产品集合，

    一个原材料集合，

    产品周期数，

    每个周期生产的产品的最大量，

    ：生产每单位产品需要的原材料的单位数，

    : 原材料的最大初始存储量，

    : 产品在周期的估计利润（如果≥0）或处理费用（如果≤0），

    : 原材料每周期每单位的存储费用，

    : 在最后的周期之后原材料的估计剩余价值或（如果≥0）处理费用（如果≤0）。

定义决策变量：

    : 在周期制造的产品的数量，

    : 在周期的开始时原材料的数量。

Maximize :在所有周期上的估计利润减去存储费用，再加上在最后周期之后剩余原材料的价值；

subject to ，: 在周期总产品数量一定不能超过指定的最大量；

                  ，: 在起初有的原材料数量不能超过指定的最大量；

                 ，: 在周期开始的原材料数量减去该周期内所消耗掉的原材料的数量一定等于周期开始时的原材料的数量。

图1-1 最大收益产品问题的代数公式

=螺帽，螺栓，垫圈

=铁，镍

，

a_{ij}	螺帽	螺栓	垫圈
铁	.79	.83	.92
镍	.21	.17	.08

c_{jt}	1	2	3	4
螺帽	1.73	1.8	1.6	2.2
螺栓	1.82	1.9	1.7	2.5
垫圈	1.05	1.1	.95	1.33

a_{ij}	b_i	d_i	f_i
铁	35.8	.03	.02
镍	7.32	.025	-.01

图1-2a 针对图1-1的两个原材料，三个产品，四个周期的数据

图 1-2b 由图1-1和图1-2a定义的线性规划问题

### 集 ###

set prd; # 产品

set raw; # 原材料

### 参数 ###

param T > 0 integer; # 产品周期数

param max_prd > 0; # 每个周期生产的产品的最大量

param units {raw,prd} >= 0; # units[i,j]是生产每单位产品j需要的原材料i的单位数

param init_stock {raw} >= 0; # init_stock[i]是原材料i的最大初始存储量

param profit {prd,1..T}; # profit[j,t]是产品j在周期t的估计利润（≥0）或处理费用（≤0）

param cost {raw} >= 0; # cost[i]是原材料i每周期每单位的存储费用

param value {raw}; # value[i]是剩余原材料i的估计剩余价值（≥0）或处理费用（≤0）

### 变量 ###

var Make {prd,1..T} >= 0; # Make[j,t]是在周期t制造的产品j的数量

var Store {raw,1..T+1} >= 0; # Store[i,t]是在周期t的开始时原材料i的数量

### 目标函数 ###

maximize total_profit:

sum {t in 1..T} ( sum {j in prd} profit[j,t] * Make[j,t] -

sum {i in raw} cost[i] * Store[i,t] )

+ sum {i in raw} value[i] * Store[i,T+1];

### 约束 ###

subject to limit {t in 1..T}: sum {j in prd} Make[j,t] <= max_prd;

subject to start {i in raw}: Store[i,1] <= init_stock[i];

subject to balance {i in raw, t in 1..T}:

Store[i,t+1] = Store[i,t] - sum {j in prd} units[i,j] * Make[j,t];

图1-3 转述成AMPL的图1-1的模型

data;

set prd := nuts bolts washers;

set raw := iron nickel;

param T := 4;

param max_prd := 123.7;

param units : nuts bolts washers :=

iron .79 .83 .92

nickel .21 .17 .08 ;

param profit : 1 2 3 4 :=

nuts 1.73 1.8 1.6 2.2

bolts 1.82 1.9 1.7 2.5

washers 1.05 1.1 .95 1.33 ;

param : init_stock cost value :=

iron 35.8 .03 .02

nickel 7.32 .025 -.01 ;

end;

图1-4 来自于图1-2a的标准AMPL格式的数据

1.2 集

    一个集可以是任意与模型有关的对象的集合。在我们的例子中两个集就是最终产品集P和原材料集R。声明语句如下：

set prd; #产品

set raw; #原材料

它们的成员在LP数据部分来指定（在图1-2a和1-4）。

    伴随prd和raw声明的注释是以#开头一直到行尾。如果模型包含了适当的注释的话，它总是很容易理解，就像在图1-3中的那样。然而为简洁起见，在接下来的正文中当声明作为例子给出时我们删掉注释。

    另外一种类型的集就是一个整数序列。在例子模型中，所有周期构成的序列1到T就是一例。在AMPL中通过表达式1..T来表示，这里T是一个参数表示周期数。一个序列集的成员显然是有序的，可以出现在算术表达式中。

    第2部分详细讨论集和索引。

1.3 参数

    参数就是与模型有关的数值。最简单的参数就是单个的独立的数值，比如前面例子中的周期数或最大总产量。

    大多数声明参数的AMPL语句也指定了某种限制。例如，周期数声明

param T>0 integer;

这也就是说T的值不喜是正整数。人们默认在代数模型中的整数限制，但是它必须对于翻译AMPL的计算机系统显式地给出。带有这种限制的数据不一致性会被翻译器拒绝。

    大多数的模型参数都不是单个值，它们是被聚合到以集为索引的数组中。初始存储量就是一个典型的例子，有一个存储水平b_i，它必须对于集R中的每个原材料i来指定。AMPL通过如下表达式指定这样关系

param init_stock{raw}>=0;

这里声明了相应于集raw的每个成员的非负参数。后面在描述约束时，相应于raw的成员i的参数用init_stock[i]来表示（AMPL总是用大括号表示整个集，用中括号表示指定的集的成员）。

    参数a_{ij}和c_{jt}是索引于两个集之上的数组。对应于c_{jt}的AMPL声明

param profit{prd,1..T};

这定义了一个参数，它索引于集prd和集1..T的所有组合之上。自然地相应于prd的成员j和1..T的成员t的参数用profit[j,t]。（AMPL大小写敏感，因此索引t和集T不产生混淆。）

    第3节详细讨论参数和表达式的操作。

1.4 变量

    一个线性规划的变量就像参数那样声明。仅有本质的区别是变量的值要通过优化来确定，然而参数的值事先要给定。

    一个典型针对储存原材料的变量声明如下

var Store{raw,1..T+1}>=0;

这定义了以raw和1..T+1所有组合为索引的一个非负变量。同参数类似，对应于raw的成员i和1..T+1的成员t的变量用Store[i,t]来表示。

    在上面所写的1..T+1中，我们使用了一个算术表达式来帮助定义一个集。就绝大部分而言，表达式可以使用在需要数值的任何地方。

1.5 目标

    一个目标函数可以是参数和变量的任意线性表达式。在图1-3中的目标的AMPL表示是从图1-1中的代数目标表达式转述而来。

AMPL的索引和的表示第一次出现在我们目标中。周期t的评估利润的和典型的表示如下

sum{j in prd} profit[j,t]*Make[j,t]

标识符j是一个哑索引，与代数符号中的对应的j有同样的目的和意思，它定义在sum的范围内，适用至紧接的项的结尾。

1.6 约束

    一个约束可以使参数和变量的任意线性等式或不等式。模型的约束使用所有同类型的表达式为其目标。虽然在图1-1中的目标函数是单个表达式，但是约束是定义在集之上的。例如在每个周期上产量限制的约束。

    对于一系列约束的AMPL表示必须指定两件事情：约束索引于其上的集和约束的表达式。于是产量限制看起来就像这样：

subject to limit{t in 1..T}: sum{j in prd} Make[j,t]<=max_prd;

紧跟关键字subject to和标识符limit之后，在大括号那个的表达式给出1..T表示索引集。标识符t是另一个哑索引，起着和代数表示中的符号同样的作用，它的有效范围是紧跟冒号之后的整个不等式。从而这对1..T中的不同的成员t，声明就指定了不同的不等式约束。

   AMPL约束表达式不需要所有的变量都在关系运算符的左边，或约束项都在右边。平衡约束就是具有更一般形式的例子：

subject to balance {i in raw, t in 1..T}: Store[i,t+1]=Store[i,t]-sum{j in prd} units[i,j]*Make[j,t];

Store[i,t+1]的引用表明集1..T的一个成员是怎样方便地使用于算术表达式中的。

    start约束可以看做周期1时Stroe变量的简单上界。大多数LP优化器通过操纵这样的界作为变量的隐式约束而不是作为显式约束矩阵的一部分表现得更有效。不过界仍然可以像其它代数约束那样来指定；界的检测和处理做为模型处理的一部分留给计算机系统来完成。

    第4节的大部分都用来讨论表示AMPL约束中的一些问题。

1.7 数据

    一旦AMPL翻译器已经读入和处理了图1-3的内容，它就准备这读数据。严格地说，有关数据的规则并不是AMPL的一部分；每个AMPL翻译器的实现都可以接受它的创作者认为合适的任何格式的数据。然而做为一个实际问题，我们希望有一个为所有的翻译器版本都接受的标准数据格式。图1-4用我们的标准数据格式显示了样例LP的一个小的数据集；它是图1-2a的一个很大程度上自明的转述。第5节详细地讨论了数据格式。

    一旦数据值被成功地读入，所有的集成员和参数的值都变成已知的。然后AMPL翻译器能够识别目标函数和约束中的变量，确定其中的系数和常数，输出适合于算法的形式。第6节描述了我们的AMPL翻译器的实现。

2. 集和索引

    索引集是任何大的线性规划模型的基础。大多数模型的组成都索引于这些集的某种组合之上；然而对于实际意义上的模型很少像图1-1中的P，R和1,…,T那样容易来描述。从而一个建模语言的设计不能在不同的集和索引表达式上提供太多的限制。任何的限制可能缩小模型能够方便表示的范围。

    根据这些考虑，我们在建模语言中提供了特别广泛的集类型。AMPL提供了针对“稀疏性”的子集，针对有序对，三元有序组和更长的元组的集，针对索引化的集簇。集能够通过使用集的并和交等运算，或者在成员上指定任意的逻辑条件来定义。参数，变量和约束都能够索引于任意的集之上；诸如求和等通用的迭代运算用同样的方式索引于集之上。

    我们通过在2.1小节介绍更简单类型的集和2.2小节的索引表达式的概念开始这一节。然后我们在2.3小节关注于有序对和其它的复合集及2.4节的索引化集簇。

    在本节和后续节的大多数例子取自四个广泛的AMPL模型，它们比放在附录中。PROD和DIST改编自为一个大的制造厂开发的多周期模型和多重物资分配模型。EGYPT是一个埃及肥料工业静态模型（Choksi，Meeraus and Stoutjesdijk 1980）。TRAIN是一个铁路系统乘客-车需求的模型（Fourer, Gertler and Simkowitz 1977, 1978）。

2.1 简单集

    任意对象的无序集通过在AMPL集声明中给定它的名字来定义：

set prd;

set center;

set whse;

    AMPL也提供了任意子集的声明。例如，DIST是被表示在分配中心坐落于仓库的子集之上、工厂坐落于分配中心的子集之上的假设上：

set dctr within whse;

set fact within dctr;

    这些子集声明既做为人们读模型时的帮助又做为数据的检查之用。也就是说如果数据包含集fact的成员而它并非集dctr的成员，那么翻译器拒绝fact的数据并报告错误。

    在DIST中实际的集声明稍微比上面的要长一些，因为它们在集标识符后包含了一个可引用的别名：

set whse 'warehouses';

set dctr 'distribution centers' within whse;

set fact 'factories' within dctr;

    别名既可以被看做是简要的解释也可以做为长的标识符被AMPL翻译器在结果报告中使用。相似的语法也可以被用在AMPL模型中的其它标识符后声明别名。为了节省空间，我们从此以后引用附录的例子时略去别名。

    简单集也可以利用其它的集或参数来定义，而不是直接来源于数据。AMPL提供了集的并、交和差等运算，就像在EGYPT中从最终产品集，中间产品集和原材料集创建产品集那样：

set commod:=c_final union c_inter union c_raw;

    也有..运算符用于构造两个整数之间的连续整数列。在PROD中，time就是以参数first开始以参数last结束的整数集：

param first >0 integer;

param last > first integer;

set time:=first..last;

    用这些运算建立的集表达式使用在AMPL模型中需要集的任何地方。例如

set c_prod within c_final union c_inter;

就声明了集c_prod，它的成员必须在集c_final或c_inter中。

2.2 索引表达式

    我们需要更一般的语法来指定参数、变量和约束索引于其上的集。同样的语法可用来描述求和和其它的运算在其上迭代的集，在下面的第三节有解释。

    在代数符号中索引通过像“for all i /in P”或“for t=1,…,T”的短语来非正式的标示。AMPL使其正式化为用大括号界定的索引表达式。就像在PROD中看到的那样，最简单的索引表达式就是刚好一个集的名字，可选的在之前可以加上哑索引：

{prd}

{t in time}

    索引表达式中的集也可通过使用集运算来指定：

{first-1..last}

{a in 1..life}

    为了与传统的代数符号一致，我们不要求哑索引的名字与任何集具有特定的关系。有时不同的集使用同样的索引名是方便的（比如PROD中t被用在几个不同的集中表示时间）或者同样的集使用不同的索引名（比如EGYPT中p1,p2,p3都作为集plant的索引）。在声明参数和变量时如果哑索引不需要就可以不要它们。

    大模型不能索引于单个集上达到充分的描述。许多参数、变量和约束最自然要索引于两个或以上的集的所有组合之上。AMPL通过在把集罗列在一个大括号中的索引表达式来表示这样的索引，比如来自于PROD的例子：

{prd,time}

{prd,first..last}

{prd,time,1..life}

{p in prd, t in time}{

{p in prd, v in 1..life-1, a in v+1..life}

集是从左至右进行解析。因此在上面的最后一个例子中，p取遍prd的所有成员，v从1到life-1，对于p和v的所有组合，a取遍v+1到life。这是一个比较自然的方式定义了一个“三角形”索引数组。AMPL也允许“方形”数组，比如在AEGYPT中的例子：

{p1 in plant, p2 in plant}

    这个表达式指定了定义在plant的成员所有的对上的索引，这取自中间工厂距离的定义中。

    实际的模型往往需要更复杂的索引，它们是由加在索引集上的某些限制而得到的。AMPL在索引表达式中通过允许指定一个逻辑条件来做到这件事。例如，DIST中的一系列约束就索引于产品的费用是零的产品-工厂对上：

{p in prd, f in fact: rpc[p,f]=0}

    在索引表达式中的条件也可以是哑索引之间的直接比较。我们可以这样

{p1 in plant, p2 in plant: p1<>p2}

来索引于来自于plant的所有不同的成员对上。

2.3 复合集

    把集看做是项的有序对或更长的组而不是单项组成的往往更为自然。例如，DIST中允许的运输路线是由有序对（d, w）组成的，其中d是分配中心集的成员，w是仓库集的成员。表示运输量的变量索引于这些对之上。

    如果每个分配中心能够运送到每个仓库，那么AMPL通过在2.2小节中介绍的表达式来操纵所有的对。的确索引表达式{dctr,whse}或{d in dctr, w in whse}精确这定了中心和仓库的所有有序对。然而在DIST模型的应用中，从中心出发的货物仅被允许运到某些相关的仓库。运输路线的集是中心-仓库对的稀疏子集。这样的情形在分配和仓储模型中是很普通的。为了自然地处理这种情形，建模语言必须能够索引于“路线集中的所有（d, w）”和类似情形的集之上。

在AMPL中运输路线集最简单地声明如下：

set rt dimen 2;

    这就是说rt是一个成员是“2维”的集：对象的有序对。然而DIST中路线并不是任意的有序对，每个成员必须是匹配的分配中心-仓库对。一个更适当的AMPL声明如下：

set whse;

set dctr within whse;

set rt within (dctr cross whse);

集算子cross表示直集，或笛卡尔积；应用到两个简单集上其结果是左操作数和右操作数的所有有序对构成的集合。从而上面的声明就是针对rt的数据必须由dcrt的成员为第一个分量、whse的成员为第二个分量的有序对组成。

    针对rt的索引表达式可以是如下两者之一

{rt}

{(d,w) in rt}

    选择哪一个取决于哑索引是否需要。索引表达式也可以是rt同其它集构成，例如

var Ship{prd, rt}>=0;

    在DIST的目标函数和约束中，这些产品货物路线变量的引用使用Ship[p,d,w]这样的形式，其中p属于prd, (d,w)属于rt。

    如果运输路线直接从数据中读取，那么建模人员必须收集路线对并把它们输入到数据文件中。然而对于DIST应用，允许的路线总是运输费用和其它数值数据的某个函数。从而一个更便利和更具可读性的AMPL模型就是通过索引表达式中的逻辑条件来定义rt。首先，运输费用通过如下语句指定：

param sc{dctr, whse}>=0;

param huge >0;

仅当sc[d,w]小于huge时，从d到w的路线是合法的，其AMPL语句如下:

set rt:={d in dctr, w in whse: sc[d,w]< huge};

    因为每个分发中心本身也是仓库，所以这个集包含了从每个分发中心到自己的路线。然而这样路线的运输费用是0，因此它们要从rt中剔除：

set rt:={d in dctr, w in whse: d<>w and sc[d,w]<huge};

    在完整的DIST例子中，如果一条路线其终点的仓库无需求量（除非仓库也是分发中心），或者如果它是“最小量限制”并且仓库装满货物的总需求量小于运输架的某个数目。整个的定义如下：

set rt:={d in dctr, w in whse:

d<>w and sc[d,w]<huge and

( w in dctr or sum{p in prd} dem[p,w]>0) and

not (msr[d,w] and sum{p in prd} 1000*dem[p,w]/cpp[p]<dsr[d])};

    更长的有序组构成的集用类似的样式来定义。例如，在TRAIN中每个铁路时刻表线路是四元组：出发城市，出发时间，到达城市，到达时间。AMPL声明如下：

set cities;

param last>0 integer;

set times:=1..last;

set schedule dimen 4;

    表示每个火车上汽车数目的变量X索引于四元组的集之上的声明如下：

var X{schedule}>=0；

    在针对这个模型的数据中（附录D）有4座城市，last是48。这样就有4×48×4×48=36864个潜在的四元组，然而schedule仅有200个成员。有序四元组对于清晰和高效的模型描述来说是必要的。

2.4 集簇

    就像参数、变量和约束能够索引于集之上一样，定义索引于其它集上的集簇也是有道理的。例如在EGYPT中，假设有肥料工厂构成的集和产品工序构成的集。然而在每个工厂，某些工序的子集被禁止。所有这些禁止的子集就是索引于工厂集之上的“集簇”。

    在AMPL中，被禁止工序的子集簇直接声明如下：

set plant;

set proc;

set p_except{plant} within proc;

    一个集p_except[pl]就定义在plant的成员工厂pl之上。所有这些集都必须是proc的子集；它们实际成员关系通过集数据的剩余部分来指定。

    AMPL的集算子也可以用类似于索引的方式来定义新的集簇。例如，第二个集簇，p_cap，表示有可用容量的工序的子集。那么在每个工厂所有可能工序的子集声明如下：

set p_pos{pl in plant}:=p_cap[pl] diff p_except[pl];

    对于plant中的每个pl，这个声明定义了独立的集p_pos[pl]，等于p_cap[pl]和p_except[pl]的差。从而对每个工厂，可能工序的子集由可用容量和不被禁止的工序组成。

    AMPL索引表达式也能用来定义索引化的集簇。考虑产品元件集unit，可以在肥料工厂集中找到，对于每个元件u和工厂pl的组合，存在初始容量icap[u,pl]。把工厂pl中有正的初始容量的元件的子集定义成m_pos[pl]是可取的：

set m_pos{pl in plant}:={u in unit: icap[u,pl]>0};

    这种更复杂的表达式在EGYPT模型中定义几个别的合适的集簇。

    集簇典型地被用在参数、变量和约束的复合索引表达式中。例如，变量Z[pl,pr]表示工厂pl的元件pr的级别。定义如下：

var Z{pl in plant, p_pos[pl]}>=0;

    更简单的索引表达式{plant, proc}也可以使用，但是我们就要对每个工厂和元件的组合来定义变量。上面的声明对每个工厂和工厂的可能元件的组合仅创建了一个变量。

    集簇和有序对很像。两者都允许模型指定两个集的笛卡尔乘积的稀疏子集。上面模型中集p_cap和集p_except能用plant cross proc中的有序对来代替，在这种方式下可能元件用集p_pos:=p_cap diff p_exceptlai来给出，元件级别变量用var Z{p_pos}>=0声明。对于有正容量的元件-工厂对类似的声明如下：

set m_pos:={u in unit, pl in plant: icap[u,pl]>0};

    EGYPT中的所有其它的集簇可做类似的转换。

    相反地，DIST模型中的集rt也可用集簇来表示：

set rt{d in dctr}:={w in whse: d<>w and sc[d,w]<huge};

对于每个分发中心d，定义rt[d]表示中心能运输货物到它那里的仓库的子集。

    几乎任意使用集簇的模型都能使用有序对来代替，反之亦然。这种选择依赖于建模者认为那哪种符号更合适和更方便。上面的例子表明有序对有时提供了更简洁但欠解释性的表达式。然而两者最重要的区别可能是在约束的描述中引起的，第4节有进一步的讨论。

3. 数值

    所有高效的大规模建模语言都必须能够描述“向量”、“矩阵”和索引于集之上的数值。如同前面提示的那样，这些值的符号描述需要显示在模型中，而它们的真实的值用一种便利的方式分离地给出（比如用第5节描述的格式）。

    在AMPL中，一个单符号数值叫做参数。因为多个数经常地被索引于集之上，所以在不致混淆的情况下我们不严格地称索引于集之上的多个数为一个参数。3.1小节以描述声明索引参数和在其上指定简单条件做为本节的开始。

    数值通过算术和逻辑运算来产生模型的目标和约束的表达式。除了相似的一元和二元运算外，传统的代数符号还提供了诸如针对加的和针对乘的等迭代运算。这些运算的AMPL做法将在3.2小节给出，对索引于集上的迭代求和的AMPL使用方法给予了特别的关注，因为这在线性规划中是必须的。我们也引入了条件（if-then-else）结构，它频繁地被使用在复杂模型的算术表达式中。

    AMPL数值表达式几乎可以用在模型中数可以出现的任何地方。然而代数模型最易于阅读和验证其目标函数和约束条件中的表达式是否保持完全的简洁。在3.3小节中，对于如何在算术表达式中利用前面定义的参数和集定义新参数给出了解释。

3.1 参数

    AMPL的参数声明描述了模型需要的某种数据，并指出模型在符号表达式中引用那些数据。语法上，参数声明由关键字param和紧跟其后的标识符和可选的针对索引、检查和其它目的的语句组成。

    索引表达式和索引参数的声明已经在第1和2节做了介绍。一个直接的例子如下

param io{commod, proc};

它定义了模型EGYPT的输入-输出系数。对于分别给定的集commod和proc中成员c和p，相应的参数值表示为io[c,p]。

不像io，绝大多数的参数都有一定的限制，典型的声明包含限定表达式，就像来自于PROD中的例子：

param iinv {prd} >= 0;

param cri {prd} > 0;

param life >0 integer;

所有的iinv的值都必须非负，cri的值必须严格正，life是个正整数。这些限制对于模型的验证是必要的，并且当翻译器到达数据的检测点时强制执行，任何的违例都会被看做错误。

    尽管像非负和整数等限制是最常用的，但是有时其它的一些限制也是需要的。在PROD中计划范围内的最后周期一定是在第一个周期之后的：

param first >0 integer;

param last >first integer;

    同样在每个周期，最大的工作人员数目不低于最小的：

param cmin {time}>=0;

param cmax {t in time}>=cmin[t];

    在很少情况简单的不等式对于表达期望的限制是不充分的。为了适应所有可能，我们在设计中包含了伴随着参数声明的check语句。例如，下面代码用来限制工作人员数目是递增的：

param cmin {first..last};

check {t in first..last} cmin[t]<=cmin[t+1];

    通常check语句可以出现在AMPL模型中任何方便的地方，并且可以在集和参数上指定任意的逻辑条件。翻译器检测所有这样的条件并报告任何的违例。

    AMPL模型的参数最常用来表示数值。然而，参数也可以声明成symbolic，用来指向任意对象比如集成员名字等。

3.2 算术和逻辑表达式

    AMPL中的算术表达式计算出浮点数。任何引用或数值字面量（17，2.71828，1.0e+30）的参数本身就是算术表达式。通常的单变量算术函数（abs，ceil，floor）和多变量算术函数（min，max）也是表达式，见TRAIN中的例子。更长的算术表达式通过使用诸如+和*等运算来建立。

    AMPL的逻辑表达式计算出真或假。它们绝大多数通过使用像=和<=等比较运算来创建。AMPL也提供了集成员关系运算in，其结果为真当且仅当它的左操作数是右操作数的成员。最后，逻辑表达式也能够通过像or和not等逻辑运算组合和扩展。表3-1汇总了这些运算和操作，按优先级递减顺序排列。

运算符	操作
^	求幂
+ - not	一元正、负、逻辑否
* / mod	乘、除、取余
sum等	迭代求和，等（见表3-2）
+ - less	加、减、非负减
in	集关系
< <= = >= > <>	比较
and	逻辑与
or	逻辑或
if … then … else …	条件计算

表3-1 算术和逻辑运算符，按优先级降序排列

迭代运算符	潜在的二元运算
sum	+
prod	*
min
max
exists	or
forall	and

表3-2 迭代运算符

    表达式也能通过在集上迭代某个运算得到。最常见就是迭代求和了，在代数符号中用∑来表示，在AMPL中是sum：

sum {p in prd} dem[p,w]

    任何的索引表达式都可以跟在sum之后。后续的算术表达式针对每个索引集的成员被计算一次，然后所有的值加起来。从而上面的来自于DIST的sum代表了仓库w的所有产品的需求量的和。sum的优先级在二元+和*之间，以致于紧跟sum的表示式包含了直到下一个+或-（不含括号子表达式）的所有内容。

    凭借sum之后可以跟任意索引表达式，AMPL对于求和提供了通用和弹性的符号表示。甚至线性约束中复杂的求和也可以直接转述，见第4节的例子。从而这种符号上的一般性实际上使语言更简单，在这里索引sum的规则同索引参数声明没有不同。AMPL用户仅仅需要学习一次索引集的语法。

    其它的满足结合律、交换律的运算也可以像sum一样被迭代计算。表3-2给出了那些AMPL中算术和逻辑运算可用的迭代运算符。返回逻辑结果的迭代运算forall的例子可以再EGYPT模型中找到：

forall {u in unit: util[u,pr]>0} u in m_pos[pl]

给定处理pr和工厂pl，这个表达式为真当且仅当满足util[u,pr]为正的每个util的成员u也是集m_pos[pl]的成员。

    最后，我们给出一个其参数值必须依赖于一些逻辑条件的例子。road[r,pl]表示从工厂pl到区域r的距离，如果工厂就在该区域则为0。从工厂到区域的运输导致固定费用加上与距离成比例的费用，但仅当工厂在区域之外。运输费用的算术表达式如下：

if road[r,pl]>0 then .5+.0144*road[r,pl] else 0

    如果在if和then之间的条件为真，那么整个表达式取then和else之间的值；而如果条件为假，那么 表达式取else之后的值。整个if…then…语句自己在任何合适的地方都充当一个操作数。EGYPT使用条件和，

(if impd_barg[pl]>0 then 1.0+.0030*impd_barg[pl] else 0)

+(if impd_road[pl]>0 then 0.5+.0144*impd_road[pl] else 0)

由进口货物的船舶和公路运输的费用组合而成。

    条件表达式的else部分可以省略，此时else 0是默认情况。这种默认在指定可选的约束项时特别方便，见第4节。紧跟else（或没有else的then）的表达式的范围是到该表达式的结尾。从而if…then…和if…then…else…语句用括号括起来会更清楚些。

3.3 计算参数

    模型的数据刚好就是目标和约束条件的系数的情况是很少见的。系数经常是参数的表达式。例如，PROD给出了在周期t所有工作组的整个正常工资：

rtr*sl*dpp[t]*cs*Crews[t]

其中rtr是每人每小时的工资额（美元），sl是一天每班的工作时数，dpp[t]是每周期的天数，cs是每个工作组的人数，Crews[t]表示周期t的工作组个数。表达式也看作约束的常数项（右端项，LP术语）。在第一个周期中对产品p的需求量约束中，如果需求量大于初始存货量，项

dem[p,first] less iinv[p]

就是两者的差，否则以0计。

    尽管任何的参数表达式可以用在目标和约束中，但是表达式最好和上面例子那样简单。当需要更复杂的表达式时，在模型中利用数据参数来定义新的、计算好的参数就更容易理解。

    计算参数的声明通常更像前面已经看到的计算集的声明。在PROD中，产品p在周期t的最小存储量是被定义成下一周期的需求量乘以pir或rir，这取决于它是否要促销：

param minv{p in prd, t in time}

:= dem[p,t+1]*(if pro[p,t+1] then pri else rir);

紧跟:=的表达式针对每个prd的成员p和time的成员t的组合进行计算，其结果赋给minv[p,t]。对周期t后分配的可用的初始存储量也是计算参数；它被看做在周期t的需求量被扣除后剩余的下一周期初始存储量（如果有的话）：

param iil{p in prd, t in time}

:= iinv[p] less sum{v in first..t} dem[p,v];

紧接着minv和iil就出现在存储需求的约束中，那里的常数项是minv[p,t]-iil[p,t]。

    按照模型的数据规范，任何为minv和iil提供显式数值的尝试都被看做错误而被拒绝。然而，如果在:=操作符后出现default，那么参数minv[p,t]和iil[p,t]的参数的部分或全部的值可以赋予其它数值，它们将覆盖计算出的值。

    作为另外的选择，我们可以利用分离的预处理程序来诸如minv和iil这些参数的值，这样它们就可以像AMPL模型中的其它参数那样来对待。当计算包含了一些比算术表达式更复杂的计算（比如算法的应用）时这种选择就无法避免了。然而我们宁愿尽可能在模型中用数据参数来表示原始的数据，然后这些数据的算术处理显式地显示在模型声明中，这样易读也易验证数据的有效性。AMPL提供的算术表达式的能力和种类倾向于鼓励这样的实践。

4. 线性规划

    线性规划中最复杂的部分就是约束。因而在4.1小节做了变量的简要说明之后，本节大部分篇幅都用于约束的声明。在4.2小节我们首先仔细解释了一些相当直接的代数约束的索引集并转述成AMPL。然后我们又说明了必须解决的三个更常用但更难的情形（双不等式，可选线性项，复合集之上的“分片”）的问题。

    做为本节的总结，给出了少量的目标函数的规范的解释。

4.1 变量

    代数线性规划模型的变量用数值数据同样的方式来描述。AMPL变量声明由关键词var，后续的标志符，同param声明一样的可选索引和限定表达式构成。

    EGYPT模型的一个变量既没有索引也没有限定：

var Psip；

然而，在大的线性规划中变量通常要索引于集上并且非负。例如，PROD包含了如下声明

var Crews{first-1..last}>=0;

var Hire{time}>=0;

var Rprd{prd,time}>=0;

var Inv{prd,time,1..life}>=0;

限定>=0表示在这些变量上的简单约束。因为非负是这样的常用，并且被几乎所有针对线性规划的算法当做默认情况来对待，所以它几乎都是做为变量声明的一部分而不是做为显式的约束。

    更一般地限定表达式可以在每个变量上指定任何下界或上界。用两个这样的表达式可以同时指定上界和下界。做为选择一个或两个这样的界可以做为约束，就像下面描述的那样。

4.2 约束

    一个线性约束就是说一个线性算术表达式等于、大于等于或者小于等于另一个线性算术表达式。典型的线性规划后很少种类的约束：10种或更少是正常的，20种就是多的了。每种约束能够用单个由参数、变量和一个或更多个哑索引所表示的符号等式或者不等式来描述。由于哑索引遍历某个集，所以一个符号表达式可以产生许多显式的约束。

    约束声明的AMPL转述有两个主要部分：索引表达式和使用-，<=，>=的比较表达式。在它们之前的是关键字subject to（可选）和约束标识符。（在模型声明中，约束标识符仅被看做语法上的占位符和具有解释该约束的有意义名字。然而标识符也是有用的，被做为优化之后针对约束的松弛和对偶变量的名字。）

    接个典型的不复杂的榆树可以在PROD中找到。对于每个计划周期，产品需要的整个工作时数不能超过所有工作组能够提供的时数：

rlim{t in time}:

sum{p in prd} pt[p]*Rprd[p,t]<=sl*dpp[t]*Crews[t];

对于每个周期的每个产品，所有前面产品的存储量加上一些没被使用的厨师存储量总共至少达到最小需求存储量：

ireq{p in prd, t in time}:

sum{a in 1..life} Inv[p,t,a]+iil[p,t]>=minv[p,t];

周期t结束时的a个周期的存储量不大于周期t-1结束时的a-1个周期的存储量：

ilim{p in prd, t in first+1..last, a in 2..life}:

Inv[p,t,a]<=Inv[p,t-1,a-1];

    AMPL翻译器决定被这些声明包含的约束中那些变量有非零的系数，然后计算这些系数和常数项的值。在我们的实现中，所有的变量被移到运算符的左端，而常数项在右端，但是这种变换建模人员并不需要关心。在参数和变量中的任何表达式都做为约束来对待，只要表达式的每一侧的关系可以解释成线性的。例如，语言允许参数乘上变量之和，或者一个变量被一个参数除。

    毫无疑问关系约束对用来表示两个不等式约束非常方便。在PROD中，每个周期雇佣的工作组的数目必须在最小值和最大值之间：

emplbnd{t in time}: cmin[t]<=Crews[t]<=cmax[t];

    如果cmin[t]小于cmax[t]那么这个约束给出了变量Crews[t]的上下界；如果cmin[t]等于cmax[t]那么Crews[t]事实上被固定在一个值上。两个更可能的例子出现在DIST中，在那里需要来完成一个周期内的定时产品的工作组数目必须落在每个工厂指定的界中：

rlim{f in fact}: rmin[f]<=

sum{p in prd} (pt[p,f]*Rprd[p,f])/(dp[f]*hd[f])<=rmax[f];

    因为仅有中间表达式包含变量，所以这样的双不等式能做为单个约束来对待。对于fact中的每个成员t，如果rmin[f]小于rmax[f]那么相关的约束就是一个不等式，其松弛就不大于rmax[f]-rmin[f]（在线性规划中的术语是range）；如果rmin[f]等于rmax[f]那么这个约束实际上就是一个等式。

    总而言之，从求解线性规划的算法的角度看，仅有四种双不等式，以四种不同的方式来处理。然而从建模者的角度看，这些都是线性约束而已。因此AMPL语言没有提供特殊的语法来区分它们，可选的模型翻译器来区分它们，见第6节的解释。

    一些约束有两个或更多的紧密关联的变体。例如在DIST中有两个运输约束的变体。在每个常规的分配中心，每个产品的转运量至少等于运出中心的量；在么个工厂分配中心，转运量至少等于运输中心的量家去在工厂中的量。通过使用条件表达式，这些变体能一起声明：

trdef{p in prd, d in dctr}

Trans[p,d]>=sum{(d,w) in rt} Ship[p,d,w]-

(if d in fact then Rprd[p,d]+Oprd[p,d]);

对于不在fact中的d，if…then…的值是0（因为没有else），因此产品项Rprd[p,d]+Oprd[p,d]被忽略。带三个变体的例子可以在每个仓库的每个产品的材料平衡约束中看到：

bal{p in prd, w in whse}:

sum{(v,w) in rt} Ship[p,v,w]+

(if w in fact then Rprd[p,w]+Oprd[p,w])=

(dem[p,w]+ (if w in dctr then sum{(w,v) in rt} Ship[p,w,v]);

第一个if表示在w中的产品，当且仅当w是工厂；第二个if表示从w到其它仓库的运输量，当且仅当w是分配中心。

上面的例子也展示了有序对被经常地使用在约束中。在bal中有两个涉及到集rt的对的和：

sum{(v,w) in rt} Ship[p,v,w]

sum{(w,v) in rt} Ship[p,w,v]

    这些和出现在约束的所有索引表达式{p in prd, w in whse}范围内，它已经定义了哑索引w。因此对特定的仓库w，第一个和是所有满足(v,w)是rt的对的v到w的运量之和，换句话说，它就是所有由分配中心运输到w的运量之和。第二个和是所有满足(w,v)是rt的对的w到v的运量之和，换句话说，它就是所有由w运输到分配中心的运量之和。简言之，第一个和的索引表达式从rt的第二个坐标中取了一些片段，而第二个和在第一个坐标中取了一些片段。在坐标中的分片安排可能在一些网络应用中看到，在那里使用集的对来表示弧。

    AMPL的对于分片对的简单符号确实引入了某种歧义，在下面的表达式

sum{(v,w) in rt} …

如果它在另外一个已经定义了哑索引w的索引表达式中（就像在bal中）那么和就是遍历在rt的分片上。另一方面，如果sum并不在任何的定义了w的范围内，那么这个和就遍历所有rt的有序对。

    做为选择我们考虑了分片之上的和的更复杂索引表达式，例如，以致于bal约束有这样的开头

bal{ p in prd, w in whse}:

sum{v in dctr: (v,w) in rt} Ship[p,v,w]+…

或者

bal{ p in prd, w in whse}:

sum{(v,w1)in rt: w1=w} Ship[p,v,w]+…

然而后者更为笨拙，同时前者仅在那些显式定义了满足(v,w)在集rt中的所有v的集的模型中才能工作。我们逐渐相信更简明分片符号的简单性和通用性是胜于由于歧义而来的任何缺点。（在TRAIN中优点更明显，那里是在有序四元组上取分片求和的。）

    集的集（不是有序对）能够用来刻画DIST。假如rt[d]被声明做可以从分配中心d直接运输到的仓库的集。那么在DIST中的约束bal有

bal{p in prd, w in whse}:

sum{v in dctr: w in rt[v]} Ship[p,v,w]+

(if w in fact then Rprd[p,w]+Oprd[p,w])=

Dem[p,w]+(if w in dctr then sum{v in rt[w]} Ship[p,w,v]);

    沿着第一坐标的分片{v in rt[w]} 显然比沿着第二个坐标的分片{v in dctr: w in rt[v]}更容易指定。在两种分片之间的对称性丢失了。

    EGYPT模型也能利用有序对或集的集来刻画，但情况不同。对的集并不能表示网络流，我们能够适当安排使它们用在约束中时总是在第一坐标上分片。对于货物的材料平衡约束提供了一个扩展的例子：

subject to mb{c in commod, pl in plant}:

sum{pr in p_pos[pl]} io[c,pr]*Z[pl,pr]

+ (if c in c_ship then

(if pl in cp_pos[c] then sum {p2 in cc_pos[c]} Xi[c,pl,p2])

+(if pl in cc_pos[c] then sum{p2 in cp_pos[c]} Xi[c,p2,pl]))

+ (if (c in c_raw and pl in cc_pos[c]) then

(( if p_imp[c]>0 then Vr[c,pl])

+( if p_dom[pl,c]>0 then U[c,pl])))

>= if(c in c_final and pl in cp_pos[c]) then sum{r in region} Xf[c,pl,r];

这集的集提供了一种自然和简明的符号，这使得它比有序对更可取。

4.3 目标函数

    线性规划的目标函数拥有约束的所有性质，除了少了一个关系运算符之外。因而除了开始使用关键字minimize或maximize代替subject to之外，目标函数的声明有着约束相同的形式。

    尽管一个线性规划仅需要一个目标函数，AMPL允许声明有任意数量的可选的目标函数，既可以是单个的或在索引集中。因而TRAIN有一个目标函数用来表示车队中车的总数，另一个目标函数用来表示按时刻表运行的车-英里数；针对已经开发的应用中，这两个目标函数借助于参数单纯形算法而交替使用。

5. 数据

    如同我们在前面的节中做的强调的那样，指定的集和参数的数据必须同AMPL组合在一起来描述一个特定的线性规划问题。数据有不同的源，但通常使用计算机来收集和组织。数据库软件经常适用于这个目的，电子表格程序也很方便。在理想的集成系统中，建模语言翻译器同数据库或电子表格软件有某种直接的联系；翻译器既能读取数据，也能够做为一个子程序被这些软件调用。

    然而即使有专用的软件界面，建模语言支持一些针对文件的简单的、标准的数据格式也是可取的。使用这样的格式有几个优点：允许翻译器运行在更广泛的环境中，鼓励教育目的的模型的交流，为算法测试收集标准模型提供便利。

    因此作为原始实现的一部分，我们设计了标准的AMPL数据文件格式。基于一维表和二维表，这个格式支持几个罗列集和参数值的自然的方式。对集和参数尽可能地使用相似的语法和概念。在我们的格式中文件可以使用任何文本编辑器创建；它们也可以相当容易地用数据库和电子表格的输出来产生。

    使用标准AMPL数据格式的例子见图1-4和附录。我们在5.1小节阐述了集成员的规范，在5.2小节阐述了参数值的规范。

5.1 集

    简单集的成员可直接指定。例如，在EGYPT模型的数据中，营养和处理的值按如下格式给出：

set nutr := N P205;

set proc := SULF_A_S SULF_A_P NITR_ACID AMM_ELEC AMM_C_GAS

CAN_310 CAN_335 AMM_SULF SSP_155;

    对集的数据既可以组织成一维表也可以组织成二维表。例如，如果p_except被定义做对集（如同2.4节建议的那样）那么上面的数据可以罗列成

set p_except:=(ASWAN,CAN_355) (HELWAN,CAN_310);

或者写成二维表如下

set p_except: CAN_335 CAN_310 :=

ASWAN + -

HELWAN - + ;

    在二维表中，+表示相应的对在集中，-表示不在。

    三元或更长的复合成员构成的集通常更为方便的表示沿着某坐标的分片。在TRAIN模型中，schedule参数是一个四元集，其成员的数据文件规范如下：

set schedule :=

(WA,*,PH,*) 2 5 6 9 8 11 10 13

12 15 13 16 14 17 15 18

16 19 17 20 18 21 19 22

20 23 21 24 22 25 23 26

24 27 25 28 26 29 27 30

28 31 29 32 30 33 31 34

32 35 33 36 34 37 35 38

36 39 37 40 38 41 39 42

40 43 41 44 42 45 44 47

46 1

(PH,*,NY,*) 1 3 5 7 9 11 11 13

13 15 14 16 15 17 16 18 ...

    模板(WA,*,PH,*)表示沿着第一个坐标WA和第三个坐标PH的分片；对于第二个坐标和第四个坐标的不同的组合的值在后面提供。上面集的等价列表式罗列如下：

set schedule:=(WA,2,PH,5) (WA,6,PH,9) (WA,8,PH,11) …

    分片表示显然更易读可能也更易创建。我们的数据格式提供了多种分片选项。有两个坐标自由的分片可以用表来描述也可以用列表。

    整个schedule集由六个不同的分片联合而成（上面仅显示了两个）。一般地，任何的一系列分片都一个定义一个集，只要没有成员被给出两次；不同的分片选项甚至可以用在同样的集的规范中。因而大的三元或四元集可以用不同的途径来指定。选择取决于建模者的习惯；例如，如果集成员保存在数据库中那么沿着排序的键就比沿着坐标更容易。

5.2 参数

    简单无索引的参数可以用显然的方式来赋值，就像图1-4中的例子：

param T:=4;

param max_prd:=123.7;

    然而绝大多数典型模型参数要索引在集上，它们的值可以用一维列表或二维表来指定。

    最基本的情况是参数索引于单个集上，比如：

param init_stock:=

iron 35.8

nickel 7.82;

    换行可以忽略，因此这个语句可以放在一行之上：

param init_stock:=iron 35.8 nickel 7.82;

    在图1-4中，init_stock同参数cost和value索引于同样的集之上。习惯上单个表可以给出所有数据：

param: init_stock cost value :=

iron 35.8 .03 .02

nickel 7.32 .025 -.01 ;

    在这种特殊形式的param语句中，每列给出了不同参数的值；参数名作为标记显示在列的顶部。

    对于索引于两个集上的参数，数据自然就使用像下面来自图1-4的二维表形式来给出：

param units: nuts bolts washers :=

iron .79 .83 .92

nickel .21 .17 .08 ;

    行标记表示第一个索引，列标记表示第二个索引。比如units[iron, bolts]是0.83。

    另外几个选项在产生或显示某种表时是有用的，特别当行是非常长时更是如此。首先，表可以转置；例如在PROD中，一个命令声明如下：

param dem{prd, first..last+1} >=0;

数据罗列如下：

param dem (tr) :

18REG 21REG 24PRO :=

1 63.8 1212.0 0.0

2 76.0 306.2 0.0

3 88.4 319.0 0.0

4 913.8 208.4 0.0

5 115.0 298.0 0.0

6 133.8 328.2 0.0

7 79.6 959.6 0.0

8 111.0 257.6 0.0

9 121.6 335.6 0.0

10 470.0 118.0 1102.0

11 78.4 284.8 0.0

12 99.4 970.0 0.0

13 140.4 343.8 0.0

14 63.8 1212.0 0.0 ;

    标记(tr)说明列标记表示第一个索引、行标记表示第二个索引，同前面的例子相比正好排列相反。同样的数据可以用非转置的形式给出，但表会有3行14列，将几乎不是那么容易显示和编辑。如果转置选项不可用，我们改变模型声明param dem {first..last+1, prd}来代替。然而我们更喜欢代数模型以更为自然的形式声明，而不关心数据是怎么表示的。

    有时转置表甚至让它的行很长。表可以按列分成几个小一点的表，就像在EYGPT模型中的参数cf75的数据那样（附录B）。或者因为打断列并不太重要，所以每个行可以沿着数据文件的几列进行划分。

    当读取数据时，AMPL翻译器对任何参数的值都不做假定。如果参数没在数据文件或模型中分配值，那么在模型中任何使用该参数的值的操作都被当做错误。这样数据中某种不一致的地方，诸如表中缺失行或列，都会在翻译器执行期间被发现。

    在一些应用中，参数某些索引是“稀疏的”：对于许多索引的组合参数的值是0。我们发现指定其默认值是0，然后显示给出非零值是方便的。例如，EGYPT模型声明厂际铁路的距离如下：

param rail_half{plant,plant}>=0;

param rail {p1 in plant, p2 in plant}:=

if rail_half[p1,p2]>0 then rail_half[p1,p2] else rail_half[p2,p1];

    指定数据如下：

set plant:=ASWAN HELWAN ASSIOUT KAFR_EL_ZT ABU_ZAABAL ;

param rail_half default 0 :

KAFR_EL_ZT ABU_ZAABAL HELWAN ASSIOUT :=

ABU_ZAABAL 85 . . .

HELWAN 142 57 . .

ASSIOUT 504 420 362 .

ASWAN 1022 938 880 518 ;

    短语default 0 表明默认值是0。参数有两种方式被赋这样的值。第一种，在表中显示 . 的的位置使用这个默认值； rail_half[ABU_ZAABAL, ABU_ZAABAL]和其它五个参数使用这样发式被赋默认值。第二种，那些没有显示在表中的参数自动赋上默认值0；这包含rail_half[ASWAN, ASWAN]和另外8个。

    另外几个默认值0的例子可以在EGYPT模型中看到。DIST中的参数使用了默认值99.99表示该路线不被允许时的大运输费用。在这些例子中，使用默认值符号而不是使用0或99.99主要是让表更具可读性；可以把 . 改成任何你喜欢的符号。