CF 505B(Mr. Kitayuta's Colorful Graph-并查集)

B. Mr. Kitayuta's Colorful Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color ci, connecting vertex ai and bi.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — ui and vi.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex ui and vertex vi directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — ai, bi (1 ≤ ai < bi ≤ n) and ci (1 ≤ ci ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (ai, bi, ci) ≠ (aj, bj, cj).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — ui and vi (1 ≤ ui, vi ≤ n). It is guaranteed that ui ≠ vi.

Output

For each query, print the answer in a separate line.

Sample test(s)

input

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

output

2
1
0

input

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

output

1
1
1
1
2

Note

Let's consider the first sample.

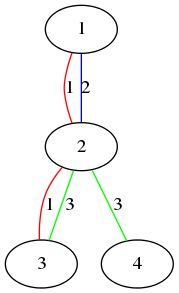The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

建m个颜色的并查集，维护点连通性。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])  
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define MAXN (100+10)
#define MAXM (100+10)
#define MAXQ (100+10)
long long mul(long long a,long long b){return (a*b)%F;}
long long add(long long a,long long b){return (a+b)%F;}
long long sub(long long a,long long b){return (a-b+(a-b)/F*F+F)%F;}
typedef long long ll;
int n,m,q;
class bingchaji  
{  
public:  
    int father[MAXN],n;  
    void mem(int _n)  
    {  
        n=_n;  
        For(i,n) father[i]=i;  
    }  
    int getfather(int x)   
    {  
        if (father[x]==x) return x;  
          
        return father[x]=getfather(father[x]);  
    }  
    void unite(int x,int y)  
    {  
        father[x]=getfather(father[x]);  
        father[y]=getfather(father[y]);  
        father[father[x]]=father[father[y]];  
    }  
    bool same(int x,int y)  
    {  
        return getfather(x)==getfather(y);  
    }  
}S[MAXM];  
int main()
{
//	freopen("Graph.in","r",stdin);
//	freopen(".out","w",stdout);
	cin>>n>>m;
	For(i,m) S[i].mem(n);
	For(i,m)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		S[c].unite(a,b);
	}
	cin>>q;
	For(i,q)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		int ans=0;
		For(j,m) if (S[j].same(u,v)) ans++;
		cout<<ans<<endl;
	}

	return 0;
}