Expectation Maximization Algorithm(EM)算法
一、基础数学知识
在正式介绍EM算法之前,先介绍推导EM算法用到的数学基础知识,包括凸函数,Jensen不等式。
1.凸函数
对于凸函数,凹函数,如果大家学过高等数学,都应该知道,需要注意的是国内教材如同济大学的《高等数学》的这两个概念跟国外刚好相反,为了能更好的区别,本文章把凹凸函数称之为上凸函数,下凸函数,具体定义如下:
上凸函数:函数f(x)满足对定义域上任意两个数a,b都有f[(a+b)/2] ≥ [f(a)+f(b)]/2
下凸函数:函数f(x)满足对定义域上任意两个数a,b都有f[(a+b)/2] ≤ [f(a)+f(b)]/2
更直观的可以看图2.1和2.2:
可以清楚地看到图2.1上凸函数中,f[(a+b)/2] ≥ [f(a)+f(b)]/2,而且不难发现,如果f(x)是上凸函数,那么-f(x)是下凸函数。
当a≠b时,f[(a+b)/2] > [f(a)+f(b)]/2成立,那么称f(x)为严格的上凸函数,等号成立的条件当且仅当a=b,下凸函数与其类似。
2.Jensen不等式
有了上述凸函数的定义后,我们就能很清楚的Jensen不等式的含义,它的定义如下:
如果f是上凸函数,X是随机变量,那么f(E[X]) ≥ E[f(X)]
特别地,如果f是严格上凸函数,那么E[f(X)] = f(E[X])当且仅当p(X=E[X]),也就是说X是常量。
那么很明显 log x 函数是上凸函数,可以利用这个性质。
有了上述的数学基础知识后,我们就可以看具体的EM算法了。
二、EM算法所解决问题的例子
在推导EM算法之前,先引用《统计学习方法》中EM算法的例子:
例1. (三硬币模型) 假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别为π,p和q。投币实验如下,先投A,如果A是正面,即A=1,那么选择投B;A=0,投C。最后,如果B或者C是正面,那么y=1;是反面,那么y=0;独立重复n次试验(n=10),观测结果如下: 1,1,0,1,0,0,1,0,1,1假设只能观测到投掷硬币的结果,不能观测投掷硬币的过程。问如何估计三硬币正面出现的概率,即π,p和q的值。
解:设随机变量y是观测变量,则投掷一次的概率模型为
![]()
有n次观测数据Y,那么观测数据Y的似然函数为
那么利用最大似然估计求解模型解,即
这里将概率模型公式和似然函数代入(1)式中,可以很轻松地推出 (1)=> (2) => (3),然后选取θ(π,p,q),使得(3)式值最大,即最大似然。然后,我们会发现因为(3)中右边多项式+符号的存在,使得(3)直接求偏导等于0或者用梯度下降法都很难求得θ值。
这部分的难点是因为(3)多项式中+符号的存在,而这是因为这个三硬币模型中,我们无法得知最后得结果是硬币B还是硬币C抛出的这个隐藏参数。那么我们把这个latent 随机变量加入到 log-likelihood 函数中,得

略看一下,好像很复杂,其实很简单,请容我慢慢道来。首先是公式(4),这里将zi做为隐藏变量,当z1为结果由硬币B抛出,z2为结果由硬币C抛出,不难发现
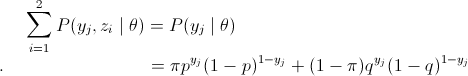
注:一下Q中有些许漏了下标j,但不影响理解
接下来公式说明(4)=> (5)(其中(5)中Q(z)表示的是关于z的某种分布,![]() ),很直接,在P的分子分母同乘以Q(zi)。最后是(5)=>(6),到了这里终于用到了第二节介绍的Jensen不等式,数学好的人可以很快发现,
),很直接,在P的分子分母同乘以Q(zi)。最后是(5)=>(6),到了这里终于用到了第二节介绍的Jensen不等式,数学好的人可以很快发现,
 就是
就是![]() 的期望值(如果不懂,可google期望公式并理解),
的期望值(如果不懂,可google期望公式并理解),
且log是上凸函数,所以就可以利用Jensen不等式得出这个结论。因为我们要让log似然函数l(θ)最大,那么这里就要使等号成立。根据Jensen不等式可得,要使等号成立,则要使![]() 成立。
成立。
再因为![]() ,所以得,c为常数,那么
,所以得,c为常数,那么
这里可以发现
OK,到这里,可以发现公式(6)中右边多项式已经不含有“+”符号了,如果知道Q(z)的所有值,那么可以容易地进行最大似然估计计算,但是Q的计算需要知道θ的值。这样的话,我们是不是可以先对θ进行人为的初始化θ0,然后计算出Q的所有值Q1(在θ0固定的情况下,可在Q1取到公式(6)的极大值),然后在对公式(6)最大似然估计,得出新的θ1值(在固定Q1的情况下,取到公式(6)的极大值),这样又可以计算新的Q值Q1,然后依次迭代下去。答案当然是可以。因为Q1是在θ0的情况下产生的,可以调节公式(6)中θ值,使公式(6)的值再次变大,而θ值变了之后有需要调节Q使(6)等号成立,结果又变大,直到收敛(单调有界必收敛),如果到现在还不是很清楚,具体清晰更广义的证明可以见下部分EM算法说明。
ps:看到上述红色内容,如果大家懂得F函数的极大-极大算法的话,就可以知道其实它们是一码事。
另外对公式(6)进行求偏导等于0,求最大值,大家可以自己练习试试,应该很简单的,这里不做过多陈述。
在《统计学习方法》书中,进行两组具体值的计算
(1)π0=0.5, p0=0.5, q0=0.5,迭代结果为π=0.5, p=0.6, q=0.5
(2)π0=0.4, p0=0.6, q0=0.7,迭代结果为π=0.4064, p=0.5368, q=0.6432
两组值的最后结果不相同,这说明EM算法对初始值敏感,选择不同的初值可能会有不同的结果,只能保证参数估计收敛到稳定点。因此实际应用中常用的办法就是选取多组初始值进行迭代计算,然后取结果最好的值。
在进行下部分内容之前,还需说明下一个东西。在上面的举例说明后,其实可以发现上述的解决方法跟一个简单的聚类方法很像,没错,它就是K-means聚类(不懂的见百度百科关于K-means算法的说明)。K-means算法先假定k个中心,然后进行最短距离聚类,之后根据聚类结果重新计算各个聚类的中心点,一次迭代,是不是很像,而且K-means也是初始值敏感,因此其实K-means算法也包含了EM算法思想,只是这边EM算法中用P概率计算,而K-means直接用最短距离计算。所以EM算法可以用于无监督学习。在下一篇文章,我准备写下典型的用EM算法的例子,高斯混合模型(GMM,Gaussian Mixture Model)。
三、EM算法
1.模型说明
考虑一个参数估计问题,现有![]() 共n个训练样本,需有多个参数θ去拟合数据,那么这个log似然函数是:
共n个训练样本,需有多个参数θ去拟合数据,那么这个log似然函数是:
可能因为θ中多个参数的某种关系(如上述例子中以及高斯混合模型中的3类参数),导致上面的log似然函数无法直接或者用梯度下降法求出最大值时的θ值,那么这时我们需要加入一个隐藏变量z,以达到简化l(θ),迭代求解l(θ)极大似然估计的目的。
2.EM算法推导
这小节会对EM算法进行具体推导,许多跟上面例子的解法推导是相同的,如果已经懂了,可以加速阅读。首先跟“三硬币模型”一样,加入隐变量z后,假设Q(z)是关于隐变量z的某种分布,那么有如下公式:

公式(7)是加入隐变量,(7)=>(8)是在![]() 基础上分子分母同乘以,(8)=>(9)用到Jensen不等式(跟“三硬币模型”一样),等号成立的条件是
基础上分子分母同乘以,(8)=>(9)用到Jensen不等式(跟“三硬币模型”一样),等号成立的条件是![]() ,c是常数。再因为
,c是常数。再因为![]() ,则有如下Q的推导:
,则有如下Q的推导:

再一次重复说明,要使(9)等式成立,则为yj,z的后验概率。算出后(9)就可以进行求偏导,以剃度下降法求得θ值,那么又可以计算新的值,依次迭代,EM算法就实现了。
EM算法(1):
选取初始值θ0初始化θ,t=0
Repeat {
E步:
M步:
}直到收敛
3.EM算法收敛性证明
那么可得如下不等式:
(10)=>(11)是因为Jensen不等式,因为等号成立的条件是θ为θt的时候得到的,而现在![]() 中的θ值为θt+1,所以等号不一定成立,除非θt+1=θt,
中的θ值为θt+1,所以等号不一定成立,除非θt+1=θt,
(11)=>(12)是因为θt+1已经使得![]() 取得最大值,那必然不会小于(12)式。
取得最大值,那必然不会小于(12)式。
所以l(θ)在迭代下是单调递增的,且很容易看出l(θ)是有上界的(单调有界收敛),则EM算法收敛性得证。
4.EM算法E步说明
上述EM算法描述,主要是参考Andrew NG教授的讲义,如果看过李航老师的《统计方法学》,会发现里面的证明以及描述表明上有些许不同,Andrew NG教授的讲义的说明(如上述)将隐藏变量的作用更好的体现出来,更直观,证明也更简单,而《统计方法学》中则将迭代之间θ的变化罗列的更为明确,也更加准确的描述了EM算法字面上的意思:每次迭代包含两步:E步,求期望;M步,求极大化。下面列出《统计方法学》书中的EM算法,与上述略有不同:
EM算法(2):
选取初始值θ0初始化θ,t=0
Repeat {
E步:
M步:
}直到收敛
(13)式中,Y={y1,y2,...,ym},Z={z1,z2,...,zm},不难看出将(9)式中两个Σ对换,就可以得出(13)式,而(13)式即是关于分布z的一个期望值,而需要求这个期望公式,那么要求出所有的EM算法(1)中E步的值,所以两个表明看起来不同的EM算法描述其实是一样的。
四、小结
EM算法的基本思路就已经理清,它计算是含有隐含变量的概率模型参数估计,能使用在一些无监督的聚类方法上。在EM算法总结提出以前就有该算法思想的方法提出,例如HMM中用的Baum-Welch算法就是。
在EM算法的推导过程中,最精妙的一点就是(10)式中的分子分母同乘以隐变量的一个分布,而套上了Jensen不等式,是EM算法顺利的形成。