积分通道特征(二)
上次,我们介绍了积分通道特征的基本方法。虽然相对于传统的HOG特征在性能和速度上面都有了一定的提升。但是,这种方法需要多次缩放图像、并且需要计算每一次缩放后的提分通道特征,这个过程需要消耗很多时间。因此,Dollar在2010提出了对这个方法的改进算法,这样相对于原始方法有了一定的提升,基本达到了实时的效果。(5fps左右)
该篇文章通过实验发现,相邻的尺度的积分通道特征之间存在一定的相似性,可以用邻近尺度的特征计算出来。文章正是基于这一思想,每个Octive内可以只计算其中一个尺度的通道特征,其他尺度的通道特征通过该尺度的特征近似计算得到。
下面,我们简要的介绍一下这篇文章:
一、近似的多尺度直方图
a)上采样的梯度直方图
假原始图像,表示上采样的图像,则,其在x方向和y方向的导数分别为为,。则我们可以理解向上采样图像的梯度变化率是原始图像的,则。那么
,
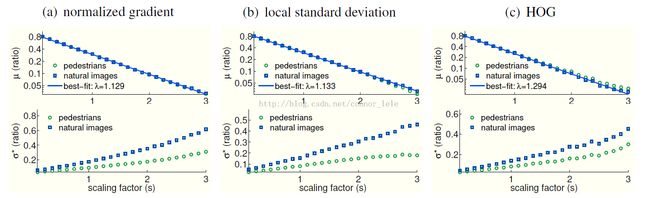
即上采样某一区域内的梯度之和是其对应原始区域梯度之和的倍。由此,我们结合直方图的定义可以得出。图1(a)给出了上采样过程中的概率分布情况,在1.99附近抖动,基本符合2倍的关系。
b)下采样的梯度直方图
由于下采样图像的过程中存在高频信息的损失,对应将会失去一部分能量。则文章认为。图1(b)给出了下采样过程中的概率分布情况,在0.32(小于0.5)附近抖动,符合预期效果。
图1
图2给出分别给出了上采样图像、原始图像以及下采样图像在8个方向的梯度直方图,可以看出前两个图像的直方图基本一致,第三个图像的存在较大的差别,主要原因是由于第三个图像中含有大量的高频信息,在下采样过程中丢失了。
图2
二、近似的多尺度特征
第一部分我们简要地说明在上采样过程、下采样过程中梯度直方图近似的过程,下面我们讲讲在积分通道特征中用到的特征的近似。
首先,在具体介绍之前,先定义几个概念。通道图像为原始图像的映射,表示为。通道特征为通道图像的区域和。表示倍下采样图像得到图像的特征。
a)指数尺度法则
该文章认为下采样图像特征与原始图像特征的差别与原始图像的尺度无关,仅与原始图像和下采样图像之间的相对尺度有关。即只和有关,通过证明及实验发现。那么当给定时,可以近似表示为
。
近似误差随着的增大而增大。当然,该公式同样适合上采样过程。这里以下采样说明。
b)估计
图1(c)给出了下采样过程中,随着的增大,梯度直方图中的变化规律。可以看出起始点并不是从1开始,至于原因可能是时虽然图像大小没变,但是使用了双线性差值对图像进行了平滑,则,根据曲线我们可以得出,。图3给出了其他三种通道特征的这一规律图。
见图2(c)和图3中方差部分。可以看出,当时,基本满足。
三、快速的多尺度检测
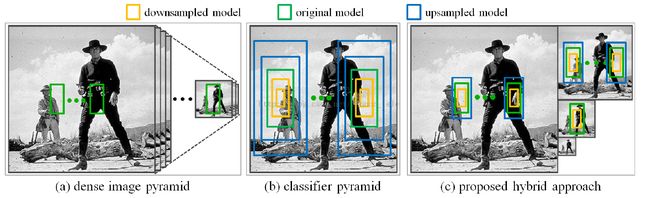
与模板固定、缩放图像的方法(图4.a)和图像固定、缩放模板的方法(图4.b)不同,该文章融合二者思想,提出先稀疏地缩放图像、后在每个图像中用多个模板检测的方法。实际中,该方法采样的尺度间距为,上采样模板所用的阈值和下采样模板所用的阈值都是原始模板的阈值近似得到的,不需要训练。该思想减少了图像缩放的次数以及通道特征计算的次数。因此,相对于原始积分通道特征方法,该方法起到了一定的加速作用。该文章表示检测速度能够达到5fps左右。
图4
四、实验结果
a)速度方法
相对于原始积分通道特征方法而言,该方法快了5-10倍。
b)检测性能
图5
五、结论
该文章主要利用了特征近似的思想,减少了图像的缩放密度以及通道特征的计算时间,从而加快了检测速度。同时这种特征近似的规律也可以应用到一些其他需要计算特征的领域中去。