重拾算法之路——线性时间选择

***************************************转载请注明出处：http://blog.csdn.net/lttree********************************************

第一章：分治与递归

线性时间选择

算法描述：

给定线性序集中n个元素和一个整数k，1 ≤ k ≤ n，要求找出这n个元素中第k小的元素。即如果将这n个元素依其线性序排列时，排在第k个位置的元素即为要找的元素。当k=1时，就是找最小元素，k=n时，就是找最大元素，当k=(n+1)/2时，就是找中位数。

算法分析：

在某些特殊情况下，很容易设计出解选择问题的线性时间算法。例如，找n个元素的最小元素和最大元素显然可以在O(n) 时间内完成。如果 k ≤ n/log(n) ，通过堆排序算法可以在 O（n+klog(n)） = O（n）时间内找出第k小元素，当k≥n-n/log(n)时也一样。

一般的选择问题，特别是中位数的选择问题似乎比找最小元素要难。但事实上，从渐进阶的意义上看，它们是一样的。一般选择问题也可以在O（n）时间内得到解决。

这次讨论 一般选择问题的一个分治算法 RandomizedSelect。这个算法是模仿 快速排序算法 设计出来的。基本思想也是 对输入数组 进行递归划分。

☆ 注意：本算法与快速排序算法 不同之处： 本算法 只对 划分出的 子数组之一 进行递归处理。 ☆

算法程序：

<span style="font-family:Comic Sans MS;">#include <iostream>
#include <ctime>
#include <cstdlib>

using namespace std;

template <class Type>
void Swap(Type& x,Type& y)
{
    Type temp = x;
    x = y;
    y = temp;
}

int Random(int l, int r)
{
    srand((unsigned)time(NULL));
    int rd = rand()%(r-l+1)+l;
    return rd;
}

// Partition函数
template <class Type>
int Partition(Type a[],int l,int r)
{
    int i = l,j = r + 1;
    Type temp = a[l];

    while(true)
    {
        while( a[++i] < temp && i < r );
        while( a[--j] > temp );
        if( i >= j )   break;
        Swap(a[i],a[j]);
    }
    a[l] = a[j];
    a[j] = temp;
    return j;
}

template<class Type>
int RandomizedPartition(Type a[],int l,int r)
{
    int tem = Random(l,r);
    Swap(a[tem],a[l]);
    return Partition(a,l,r);
}

template <class Type>
Type RandomizedSelect(Type a[],int l,int r,int k)
{
    if(l == r)  return a[l];
    int tem,j;
    tem = RandomizedPartition(a,l,r);
    j = tem - l + 1;
    if(k <= j)  return RandomizedSelect(a,l,tem,k);
    else    return RandomizedSelect(a,tem+1,r,k-j);
}</span>

这里面的函数：

——Swap   交换两个元素的值

——Random 取两个区间内的随机数

——Partition 在快排中也有见过，就是以第一个数为标准，小于它的在它左面，大于它的在它右面

——RandomizedPartition 加了随机数的Partition，这次就不一定以第一个数为标准了，在范围内随机一个数为标准

——RandomizedSelect 求l到r，第k小的元素

算法讲解：

在上述算法程序中，执行完函数RandomizedPartition后，数组a[l:r]会被分为两个部分：a[l:tem] 和 a[tem+1:r]，但左面部分的每一个元素都不大于 右面部分的任何一个元素。

接着计算左面部分元素个数j，如果 k ≤ j ，则a数组中第k小的元素坐落在子数组a[l:tem]中。反之坐落在a[tem+1:r]中。所以只需要对一个子数组进行扩展。

在最坏的情况下，算法RandomizedSelect需要 Ω(n^2)的计算时间。尽管这样，该算法的平均性能很好，因为随机划分数RandomizedPartition使用了随机数产生器Random，在这个条件下可以证明，算法RandomizedSelect可以在O(n)平均时间内找出n个输入元素中的第k小元素。

算法优化：

接下来讨论一个可以在最坏情况下用O(n)时间就完成选择任务的算法Select。

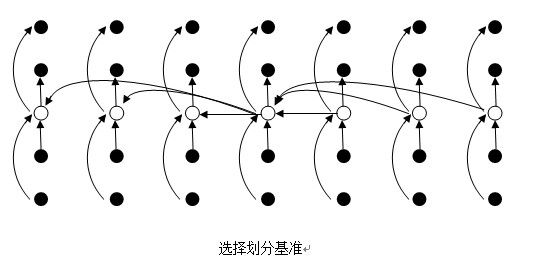
如果能在线性时间内找到一个划分基准，使得按照这个基准所划分出的两个子数组长度都至少为元数组长度的 m 倍（0 < m < 1），那么在最坏情况下用O（n）时间就可以完成选择任务。

例如，m=9/10 ，算法递归调用所产生的子数组长度至少缩短1/10。所以，在最坏情况下，算法所需的时间为T（n） 满足递归式T(n) ≤ T(9n/10)+O(n)。由此可得T（n）=O（n）。

算法步骤如下：

<1> 将所有的数n个以每5个划分为一组共组，将不足5个的那组忽略，然后用任意一种排序算法，因为只对5个数进行排序，所以任取一种排序法就可以了。将每组中的元素排好序再分别取每组的中位数，得到个中位数。

  <2> 取这个中位数的中位数，如果是偶数，就找它的2个中位数中较大的一个作为划分基准。

<3> 将全部的数划分为两个部分，小于基准的在左边，大于等于基准的放右边。在这种情况下找出的基准x至少比个元素大。因为在每一组中有2个元素小于本组的中位数，有个小于基准，中位数处于，即个中位数中又有个小于基准x。因此至少有个元素小于基准x。同理基准x也至少比个元素小。而当n≥75时≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4。

程序：

<span style="font-family:Comic Sans MS;">template <class Type>
void Swap(Type& x,Type& y)
{
    Type temp = x;
    x = y;
    y = temp;
}
int Random(int l, int r)
{
//    srand((unsigned)time(NULL));
    int rd = rand()%(r-l+1)+l;
    return rd;
}
template <class Type>
int Partition(Type a[],int l,int r,Type x)
{
    int i = l-1,j = r + 1;

    while(true)
    {
        while(a[++i]<x && i<r);
        while(a[--j]>x);
        if(i>=j)    break;
        Swap(a[i],a[j]);
    }
    return j;
}
template <class Type>
void BubbleSort(Type a[],int l ,int r )
{
    for( int j = l ; j < r-1 ; ++j )
        for( int i = l ; i < r-1-j ; ++i )
            if( a[i] > a[i+1] )
                Swap(a[i],a[i+1]);
}
template <class Type>
Type Select( Type a[],int l ,int r,int k )
{
    if( (r-l) < 75 )    {
        // 元素小于75个，直接用某个排序排一下就行（这里用的冒泡）
        BubbleSort(a,l,r);
        return a[l+k-1];
    }
    for( int i = 0 ; i <= (r-l-4)/5 ; ++i ) {
        //将元素每5个分成一组，分别排序，并将该组中位数与a[l+i]交换位置
        //使所有中位数都排列在数组最左侧，以便进一步查找中位数的中位数
        BubbleSort(a,l+5*i,l+5*i+4);
        Swap(a[l+5*i+2],a[l+i]);
    }
    // 找中位数的中位数
    Type x = Select(a,l,l+(r-l-4)/5,(r-l-4)/10);
    int i = Partition(a,l,r,x);
    int j = i-l+1;
    if(k<=j)
        return Select(a,l,i,k);
    else
        return Select(a,i+1,r,k-j);
}</span>

***************************************转载请注明出处：http://blog.csdn.net/lttree********************************************