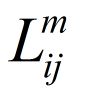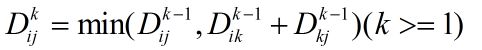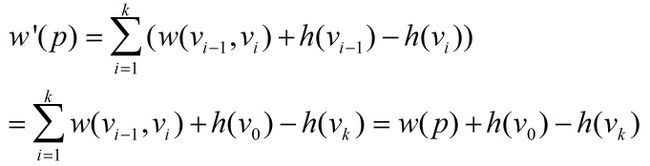图算法---每对顶点间最短路径

前言：

在前面的单源算法中，假定采用图的邻接表表示法。于此不同，本章中的大多数算法均采用邻接矩阵表示法。为方便起见，假设顶点编号为1,2,3,4，....|V|。于是我们用一个n*n的矩阵W，表示有n个顶点的有向图G=（V,E)中边的权值。其中                   0   如果i = j

                 Wij = 有向边（i，j）的权值  如果i != j ,且(i,j)属于E

                             正 无穷如果i != j,且(i,j) 不属于E

前两个算法是用动态规划方法来分析的，利用到矩阵的性质。

在讨论之前，有必要对邻接矩阵表示法建立一些约定。首先，一般假设输入图G=(V,E)有n个顶点，所以n = |V|。其次，我们按常规用大写字母来表示矩阵，例如W,L，用带有下标的小写字母来表示矩阵的元素，如Wij。有些矩阵带有括号的上标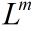 ,用来表示迭代,rows[A] = n 。

25.1、最短路径与矩阵乘法(该算法使用动态规划分析)

1、最短路径子结构：对于图G=(V,E)，用一个n*n的矩阵W，表示有n个顶点的有向图G=（V,E)中边的权值。考察顶点i到j的一条最短路径p，假设p之多包含m条边。假设图中不存在负权回路，则m是有限值。如果i = j，则路径p权值为0，且没有边。若顶点i和顶点j是不同顶点，则把路径p分解为i---->k->j,其中i---->k是路径p‘，其中p’至多有m-1条边。由引理24.1可知  min(i,j) = min(i,k) + wij

2、每对顶点间最短路径问题的一个递归解

      现在设   为是从顶点i到j的至多m条边的任何路径的权值最小值。其中

     公式（25.2） 递归解：

      结论：不难得出，当m >= n-1时，即从顶点i到j的至多有n-1条边的最小权重路径，就是顶i到j的最短路径。

     

3、算法描述（到这一步我想大家应该都很清楚了）

      

#定义25.2公式计算函数，L为L(m-1),W为图G=(V,E)的权重矩阵，返回Lm,其中L是|V|*|V|矩阵，W是|V|*|V|矩阵
def extend_shortest_paths(L,W,P):
    #L1是返回矩阵,初始化L1为n*n矩阵
    import copy
    L1 = copy.deepcopy(W)
    for i in range(0,len(L1)):
        for j in range(0,len(L1)):
            L1[i][j] = None
            for k in range(0,len(L)):
                if W[k][j] == None or L[i][k] == None:
                    continue
                if L1[i][j] == None or L[i][k] + W[k][j] < L1[i][j]:
                    L1[i][j] = L[i][k] + W[k][j]
                    P[i][j] = k
    return L1
#每对顶点间最短路径算法
def slow_ALL_PAIRS_SHOTEST(W):
    import copy
    n = 1
    L = copy.deepcopy(W)
    #定义n*n矩阵P，p[i][j]存储i到j的最短路径上j的前一个顶点
    P = copy.deepcopy(W)
    for i in range(0,len(W)):
        for j in range(0,len(W)):
            if i == j:
                P[i][j] = -1
            if W[i][j] != None:
                P[i][j] = i
    while n < len(W)-1:
        L = extend_shortest_paths(L,W,P)
        n = n+1
    return (L,P)
if __name__ == "__main__":
    W = [[0,2,3,4],[1,0,3,4],[1,2,0,4],[-1,-1,-1,0]]
    ret = slow_ALL_PAIRS_SHOTEST(W)
    print ret[0]

4、算法优化（通过矩阵相乘的性质优化该算法）

      

 25.2 Floyd_Warshall算法(动态规划方法进行分析)

1、最短路径的结构：

    该算法考虑最短路径上的中间顶点，其中简单路径P=(v1,v2,v3.Vn)上的中间顶点是除v1、v2以外P上的任何一个顶点。

    floyd_warshall算法主要基于以下观察。设G的顶点V = {1,2,...,n},对某个K考虑顶点的子集{1,2,...,K}。对任意一对顶点i，j属于V。考察从i到j且所有中间顶点属于{1,2,...K}的所有路径，设p是其中一条最小权值路径（路径p是简单的）FLoyd_warshall算法利用了路径P与i到j之间的最短路径之间的联系。这一联系依赖于K是否是路径P上的一个中间顶点。

   情况1：K不是路径P的中间顶点，因此路径P的所有中间顶点属于集合（1,2，....,k-1)。因此从顶点i到j满足中间顶点属于（1，....,K-1)的最短路径，同样是从顶点i到j满足中间顶点属于（1，...,K)的最短路径

   情况2：K是路径P的中间顶点，因此路径可拆分为 P1: i到K的的部分，P2：K到j的部分。可知，P1、P2所有的中间顶点属于（1，...,K-1)。

2、一个递归解

对于图G=(V,E),矩阵式图G的边权重矩阵，对顶点编号1,2,...,|V|,假设存储顶点i到j且中间顶点属于集合(1,2,...,K)的所有路径中的最小权重值。

其中= ，意味着顶点i到顶点j没有中间顶点，所以直接等于

我们可以得出一个递归解：

最后我们可以得出结论：

,顶点i到j的所有中间顶点属于(1,2,..,n)的最短路径，就是顶点i到j的最短路径

3、算法描述和分析

3.1、时间复杂度O(n^3)

3.2、额外空间存储2*(n*n)

def floyd_warshall(W):
    import copy
    #需要两个n*n矩阵的额外存储
    D_in =  copy.deepcopy(W)
    D_ret = copy.deepcopy(W)
    k = 0
    while k < len(W):
        tmp = D_ret
        D_ret = D_in
        D_in = tmp
        for i in range(0,len(D_ret)):
            for j in range(0,len(W)):
                D_ret[i][j] = min(D_in[i][j],D_in[i][k] + D_in[k][j])
        k = k+1
    print D_ret

4、构造最短路径（这里我们通过获得前驱矩阵来计算最短路径）

定义为i到j的中间顶点属于集合(1,2,...k)的最短路径P

定义存储路径P上顶点j前一个路径。

我们可知，= i 或者 nil，如果有边(i,j)等于i，不存在边(i,j)等于nil

  递归公式：

5、习题

5.1、计算图的闭包：已知有一个有向图G=(V,E),顶点集合V={1,2,...,n)，物品，我们可能希望确定对所有顶点对i,j属于V，图G中是否存在一条从i到j的路径。G的传递闭包定义为图G*=(V,E*),其中E*={(i,j):i到j有路径。？

5.2、利用floyd_warshall算法，判断一个图是否有负权回路？

个人思路： 

1、先利用 floyd_warshall算法求解路径的最短路径，得到举国矩阵D

2、判断D[i][i] 是否 == 0

3、如果有D[i][i]小于0，则有负权回路

25.3稀疏图上的JOHNSON算法

1、引理25.1（重赋权技术）：

已知带权有向图G=(V,E),加权函数w：E->R,设h：V->R是将顶点映射到实数的任意函数。对每条边(u,v)属于E，定义 w'(u,v) = w(u,v)+h(u) - h(v)。另p={v0,v1,...,vk}为从顶点v0到vk的任意一条路径。则p是利用加权函数w从v0到vk的一条最短路径，当且仅当p也是利用w‘的一条最短路径。亦即，w(p) = min(v0,vk),当且仅当w'(p)=min(v0,vk)。

另外，使用加权函数w时，G中存在一条负权的回路，当且仅当使用加权函数w’，G中存在一条负权的回路。

证明：

1.1、首先证明 w'(p) = w(p) + h(v0) - h(vk)

1.2、

w'(p) = w(p) + h(v0) - h(vk)

2、Johnson算法

算法描述:

2.1、通过重新赋权技术，使得每条边的权重大于0，如果有负权回路，返回false

2.2、对每个顶点调用Dijkstra算法计算每对顶点的最短路径

3、Johnson算法关键步骤：如何重新赋权，确保每条边权重大于0。

对于图G=(V,E),构造一个额外顶点s，构造一个新图G'=(V',E'), V' = V U s，E’ = E U{(s,v):v属于E}。

w(s,v) = 0.

现在假设G和G'都不含有负权回路。定义v 属于V‘，h(v) = min(s,v)。  因为h(v) <=  h(u) +w(u,v)，所以，我们定义w'(u,v) = w(u,v) + h(u) - h(v)  >= 0

既然大于0了，那么这个w’满足我们要求了

证明：当且仅当G'存在负权回路，G也存在负权回路。

因为所以便(s,v),v属于E，这些边都是0权路径，所以加入顶点s和边(s,v)后不影响G的回路性质。

4、算法描述(待写）