HDU 5365 Run ——BestCoder Round #50(div.1 div.2)
Run
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Problem Description
AFA is a girl who like runing.Today,he download an app about runing .The app can record the trace of her runing.AFA will start runing in the park.There are many chairs in the park,and AFA will start his runing in a chair and end in this chair.Between two chairs,she running in a line.she want the the trace can be a regular triangle or a square or a regular pentagon or a regular hexagon.
Please tell her how many ways can her find.
Two ways are same if the set of chair that they contains are same.
Please tell her how many ways can her find.
Two ways are same if the set of chair that they contains are same.
Input
There are multiply case.
In each case,there is a integer n(1 < = n < = 20)in a line.
In next n lines,there are two integers xi,yi(0 < = xi,yi < 9) in each line.
In each case,there is a integer n(1 < = n < = 20)in a line.
In next n lines,there are two integers xi,yi(0 < = xi,yi < 9) in each line.
Output
Output the number of ways.
Sample Input
4 0 0 0 1 1 0 1 1
Sample Output
1
Source
BestCoder Round #50 (div.2)
附上该题对应的中文题
Run
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/65536 K (Java/Others)
问题描述
小花是一个热爱健身的姑娘,这天她下载了一个跑步软件,这个软件可以记录下小花跑步的轨迹。小花决定去公园跑步。公园里有许许多多的座椅,小花希望在一些座椅休息一下,并且她在两条座椅之间只跑直线。小花是一个完美主义者,她希望自己最后的轨迹是一个正三边形或者正四边形或者正五边形或者正六边形。小花会从某条座椅开始打开跑步软件,并在回到这个座椅后关闭。 请问小花有多少种跑法。注:若两种跑法经过的座椅集合相同则认为是一种跑法。且经过一条座椅时没有必要一定停下来
输入描述
输入有多组数据 每组数据第一行为一个n(1 < = n < = 20)表示座椅数量 接下来n行,每行两个整数xi,yi(0 < = xi,yi < = 8)表示座椅的坐标
输出描述
输出方案数
输入样例
4 0 0 0 1 1 0 1 1
输出样例
1
/****************************************************/
出题人的解题思路:
出题人简单粗暴地直接说明了整点是不能构成正三角形、正五边形和正六边形的,相信比较多的人对此都有疑问,为什么不能构成呢,下面我给出不能构成正三角形的证明
反证法:假设存在坐标平面上的三个整点,组成了正三角形
则将其平移,将其一个顶点与坐标原点重合,则另两个顶点仍然是整点
设一个非原点的顶点M坐标为(a,b) ,另一个顶点为N(c,d), a、b、c、d都是整数
则MO的斜率=,倾斜角=arctan()
则NO的倾斜角=arctan()+
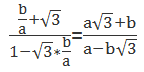
因为a、b不全等于0,所以c和d至少有一个是无理数
这和c、d都是整数矛盾
所以坐标平面上的三个整点,一定不能组成正三角形
至于正五边形和正六边形,就交给你们自己去证明了。所以此题只要暴力枚举每四个点,判断能否形成正方形即可,而正方形的判断依据是四条边均相等,对角线相等,且其平方是边平方的两倍。
上代码,有疑问可以提出来
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
#define ll __int64
using namespace std;
const int N = 25;
const int inf = 1000000000;
const int mod = 1000000007;
int x[N],y[N],s[6];
int sqare(int x1,int y1,int x2,int y2)
{
return (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1);
}
bool judge(int i,int j,int k,int l)
{
int t=0;
s[t++]=sqare(x[i],y[i],x[j],y[j]);
s[t++]=sqare(x[j],y[j],x[k],y[k]);
s[t++]=sqare(x[k],y[k],x[l],y[l]);
s[t++]=sqare(x[l],y[l],x[i],y[i]);
s[t++]=sqare(x[i],y[i],x[k],y[k]);
s[t++]=sqare(x[l],y[l],x[j],y[j]);
sort(s,s+6);
if(s[0]==s[1]&&s[2]==s[3]&&s[1]==s[2]&&s[4]==2*s[0]&&s[5]==s[4])
return true;
return false;
}
int main()
{
int n,i,j,k,l,t;
while(~scanf("%d",&n))
{
t=0;
for(i=1;i<=n;i++)
scanf("%d%d",&x[i],&y[i]);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
for(k=j+1;k<=n;k++)
for(l=k+1;l<=n;l++)
if(judge(i,j,k,l))
t++;
printf("%d\n",t);
}
return 0;
}菜鸟成长记
