动态规划——装配线调度
问题的描述:
汽车生产工厂共有两条装配线,每条有 n 个装配站;装配线 i 的第 j 个装配 站表示为 Si,j,在该站的装配时间为 ai,j。一个汽车底盘进入工厂,然后进入装配 线 i(i 为 1 或 2) ,花费时间为 ei。在通过一条线的第 j 个装配站后,这个底盘来 到任一条线的第(j+1)个装配站。如果它留在相同的装配线,则没有移动开销; 如果它移动到另一条线上,则花费时间为 ti,j。在离开一条线的第 n 个装配站后, 完成的汽车花费时间 xi 离开工厂。带求解的问题是:确定应该在装配线 1 内选择 哪些站,在装配线 2 内选择哪些站,才能使汽车通过工厂的总时间最小。

动态规划的解题步骤有四步:
步骤1:描述最优解的结构的特征 .
步骤2:利用子问题的最优解来递归定义一个最优解的值
步骤3:计算最快时间
步骤4:构造通过工厂的最快路线
公式表达的很清晰,这个公式就是用上面提到的最优解结构的求法定义出来的。
根据递归的定义以及上面的内容,也可以得出要求出到达每一个装配站的最优时间的递归公式
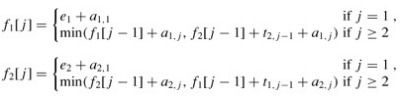
这样就可以求出最终的min_f了,也就是第三步的计算最优解的值就出来了。因为还有第四步,就是构造最优解,在这道题目中,就是要构造出这条时间花费最小的路线。为了可以构造出这条路线,还要记录下到达每一个装配站时,上一个装配站是属于哪一条装配线的,也就是上面的数组L[2][n]的定义。
下面是代码,数据是按照下面这张图输入的

汽车生产工厂共有两条装配线,每条有 n 个装配站;装配线 i 的第 j 个装配 站表示为 Si,j,在该站的装配时间为 ai,j。一个汽车底盘进入工厂,然后进入装配 线 i(i 为 1 或 2) ,花费时间为 ei。在通过一条线的第 j 个装配站后,这个底盘来 到任一条线的第(j+1)个装配站。如果它留在相同的装配线,则没有移动开销; 如果它移动到另一条线上,则花费时间为 ti,j。在离开一条线的第 n 个装配站后, 完成的汽车花费时间 xi 离开工厂。带求解的问题是:确定应该在装配线 1 内选择 哪些站,在装配线 2 内选择哪些站,才能使汽车通过工厂的总时间最小。

动态规划的解题步骤有四步:
步骤1:描述最优解的结构的特征 .
步骤2:利用子问题的最优解来递归定义一个最优解的值
步骤3:计算最快时间
步骤4:构造通过工厂的最快路线
在这之前先说明要用到的一些符号的定义:
进入每条装配线的时间存在数组e[]中
出每条装配线的时间存放在数组x[]中
每条装配线的每个装配站的时间存放在数组a[2][n]中,a[1][4]就代表第2条装配线的第5个装配站。
从一条装配线的某一个装配站,到另一条装配线的下一个装配站的时间,存放在数组t[2][n]中,
例如,t[0][4]就代表从第一条装配线的第五个装配站转移到第二条装配线的第六个装配站的时间。
计算最短时间的过程中,用数组f[2][n]保存过程的中间解。例如,f[1][3]就保存了到达第二条
装配线的第四个装配站的最短时间。然后用min_f保存最终的结果,也就是最短的生产时间。
为了输出整条最短时间的生产装配站序列,再设一个数组L[2][n],其中L[1][5]就表示到达第二条装配
线的第六个装配站的前一个装配站,也就是第五个装配站是属于哪一条装配线的,是1还是2.然后
fin_l保存最终生成完成时,是从哪一条装配线出来的。
最终我们要求的结果就是min_f(就是下面图中的f*),经过工厂n个装配站的最短时间
公式表达的很清晰,这个公式就是用上面提到的最优解结构的求法定义出来的。
根据递归的定义以及上面的内容,也可以得出要求出到达每一个装配站的最优时间的递归公式
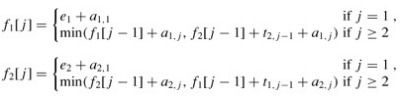
这样就可以求出最终的min_f了,也就是第三步的计算最优解的值就出来了。因为还有第四步,就是构造最优解,在这道题目中,就是要构造出这条时间花费最小的路线。为了可以构造出这条路线,还要记录下到达每一个装配站时,上一个装配站是属于哪一条装配线的,也就是上面的数组L[2][n]的定义。
下面是代码,数据是按照下面这张图输入的

#include <iostream>
#include <stack>
using namespace std;
void pr_minLine(int l[][6],int n,int fin_l)
{
stack<int> s;
int i=fin_l;
s.push(i);
for(int j=n-1;j>=1;--j)
{
i=l[i][j];
s.push(i);
}
for(int j=0;j<n;++j)
{
cout << "line " << s.top()+1<< " station: " << j+1 << endl;
s.pop();
}
}
int fastWay(int a[][6],int t[][6],int e[],int x[],int f[][6],int l[][6],int n)
{
int fin_l,min_f;
f[0][0]=e[0]+a[0][0];
f[1][0]=e[1]+a[1][0];
for(int i=1;i<n;++i)
{
if( f[0][i-1]+ a[0][i] <= f[1][i-1] +t[1][i-1]+ a[0][i] )
{
f[0][i]=f[0][i-1]+ a[0][i] ;
l[0][i]=0;
}
else
{
f[0][i] = f[1][i-1] +t[1][i-1]+ a[0][i];
l[0][i] = 1;
}
if (f[1][i - 1] + a[1][i] <= f[0][i - 1] + t[0][i - 1] + a[1][i])
{
f[1][i] = f[1][i - 1] + a[1][i];
l[1][i] = 1;
}
else
{
f[1][i] = f[0][i - 1] + t[0][i - 1] + a[1][i];
l[1][i] = 0;
}
}
min_f= f[0][n-1] + x[0] <= f[1][n-1] + x[1] ? (fin_l=0,f[0][n-1] + x[0]) : (fin_l=1,f[1][n-1] + x[1]);
pr_minLine(l,n,fin_l);
return min_f;
}
int main() {
int a[2][6]={{7,9,3,4,8,4},{8,5,6,4,5,7}};
int t[2][6]={{2,3,1,3,4},{2,1,2,2,1}};
int e[2]={2,4};
int x[2]={3,2};
// f[i][j] 表示到第i条线的第j个站,最小要花多长时间
// l[i][j] 表示到第i条线的第j个站,是从哪个哪条线进来的
// fin_l 表示最后是从哪条线出来的
int f[2][6],l[2][6];
cout << "\n最短时间:" << fastWay(a,t,e,x,f,l,6) << endl;
return 0;
}