HDU 1542 Atlantis(线段树:扫描线)
HDU 1542 Atlantis(线段树:扫描线)
http://acm.hdu.edu.cn/showproblem.php?pid=1542
题意:
二维平面有n个平行于坐标轴的矩形,现在要求出这些矩形的总面积. 重叠部分只能算一次.
分析:
线段树的典型扫描线用法.
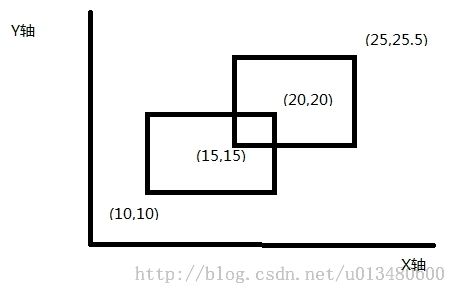
首先假设有下图两个矩阵,我们如果用扫描线的方法如何计算它们的总面积呢?
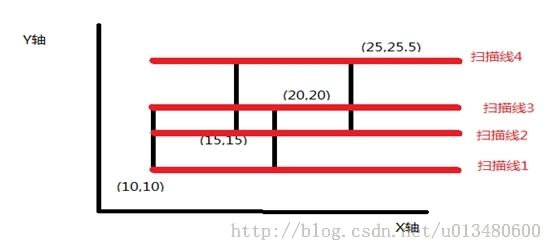
首先我们将矩形的上下边分为上位边(即y坐标大的那条平行于x轴的边),和下位边(y坐标小的平行于x轴的边).然后我们把所有矩形的上下位边按照他们y坐标从小到大排序,可以得到4条扫描线:
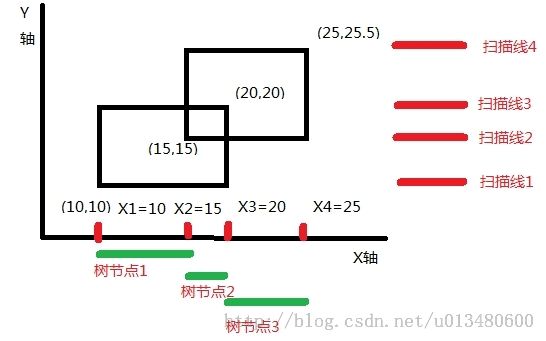
又因为上面2个矩形有4个不同的浮点数x坐标,所以我们需要把x坐标离散化,这样才能用线段树来维护信息.所以我们这样离散化:
由上图可知,4个不同的x坐标把x轴分成了3段有效的区间.这里要注意我们线段树中每个叶节点(控制区间[L,L])不是指X[L]坐标,而是指区间[X[L],X[L+1]].线段树中其他节点控制的区间[L,R],也是指的x坐标轴的第L个区间到第R个区间的范围,也就是X[L]到X[R+1]坐标的范围.
然后我们Y坐标从小到大的顺序读入每条扫描线,并维护当前我们所读入的所有扫描线能有效覆盖X轴的最大长度sum[1].这里特别要注意如果我们读入的扫描线是矩形的下位边,那么我们就使得该范围的标记cnt位+1,如果是上位边,那么该范围的cnt就-1.所以如果cnt=0时,表示该节点控制的范围没有被覆盖,只要cnt!=0 就表示该节点控制的几块区间仍然被覆盖.
下面依次读入每条矩阵边,来一一分析,首先是读入第一条矩阵边:
我们读入了矩形1的下位边,那么该区域的cnt就+1=1了,所以该区域[10,20]就被覆盖了,然后可以推出整个区域被覆盖的长度是10.再根据第二条扫描线离第一条扫描线的高度差为5.所以不管你第二条扫描线是哪个矩形的什么边,或者能覆盖到X轴的什么范围,我上图中蓝色的矩形面积肯定是要算到总面积里面去的.即总面积ret+=sum[1]*(扫描线2的高度-扫描线1的高度). (想想看是不是这样).
下面读第二条扫描线:
由于第二条扫描线也是下位边,所以[15,20]和[20,25]的cnt+1.使得我们覆盖的范围变成了[10,25]了,并且第3条扫描线在20高度,所以这次我们必然增加的面积是上面深蓝色的长条=sum[1]*(扫描线3的高度-扫描线2的高度).
下面我们要读第三条扫描线了:
由于第三条扫描线是区间[10,20]的上位边,所以对应区间的cnt要-1,所以使得区间[10,15]的cnt=0了,而[15,20]区间的cnt-1之后变成了1.[20,25]的cnt仍然为1,不变.所以当前覆盖的有效x轴长度为10,即区间[15,25].所以增加的面积是图中褐色的部分.
到此,矩形的面积和就算出来了.由于对于任一矩形都是先读下位边(cnt+1),再读上位边(cnt-1)的,所以在更新线段树的过程中,任意节点的cnt都是>=0的.
下面说代码实现部分:
首先建立一个node结构体用来保存每条扫描线,node中有信息:
l: 表示扫描线的左端x坐标
r:表示扫描线的右端x坐标
h: 表示扫描线的高度
d: 为1或-1,标记扫描线是矩形的上位还是下位边.
我们首先读入所有矩形的信息,每读入一个矩形信息我们就更新两条扫描线,并且把矩形的两个端点x坐标放入X[MAXN]数组中,
然后我们对node和X都排序,node按h值从小到大排序.
X按从小到大排序.
然后我们在X的本地数组内,对X去重,并且用k表示一共有多少个X.
当我们需要找到第i个区域的两端点坐标时,只需要X[i]和X]i+1].
线段树维护cnt(根本信息)和sum两个信息,其中sum为double,cnt为int型.
cnt: >=0时表示本节点控制的区域内下位边个数-上位边个数的结果.如果==-1时,表示本节点左右子树的上下位边数不一致.
sum: 本节点控制的区域内cnt值不为0的区域总长度.
线段树操作:
PushDown(i,l,r):如果cnt!=-1,那么下放cnt信息,并更新子节点的sum信息.
PushUp(i,l,r): 根据子节点的cnt值和sum值更新父节点的cnt和sum值.
update(ql,qr,v,i,l,r): 使得[ql,qr]与[l,r]区间的公共部分cnt值+v.
如果ql<=l && r<=qr 且 cnt[i]!=-1的话,直接更新并return
否则先PushDown
在一次递归更新左右儿子
最后PushUp.
AC代码:0ms.
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=2222;
#define lson i*2,l,m
#define rson i*2+1,m+1,r
#define root 1,1,k-1
double X[MAXN];
struct node
{
double l,r,h;
int d;
node(){}
node(double a,double b,double c,int d): l(a),r(b),h(c),d(d){}
bool operator <(const node &b)const
{
return h<b.h;
}
}nodes[MAXN];
int cnt[MAXN*4];
double sum[MAXN*4];
void PushDown(int i,int l,int r)
{
int m=(l+r)/2;
if(cnt[i]!=-1)
{
cnt[i*2]=cnt[i*2+1]=cnt[i];
sum[i*2]= (cnt[i]?(X[m+1]-X[l]):0) ;
sum[i*2+1]= (cnt[i]?(X[r+1]-X[m+1]):0) ;
}
}
void PushUp(int i,int l,int r)
{
if(cnt[i*2]==-1 || cnt[i*2+1]==-1)
cnt[i]=-1;
else if(cnt[i*2] != cnt[i*2+1])
cnt[i]=-1;
else
cnt[i]=cnt[i*2];
sum[i]=sum[i*2]+sum[i*2+1];
}
void build(int i,int l,int r)
{
if(l==r)
{
cnt[i]=0;
sum[i]=0.0;
return ;
}
int m=(l+r)/2;
build(lson);
build(rson);
PushUp(i,l,r);
}
void update(int ql,int qr,int v,int i,int l,int r)
{
if(ql<=l && r<=qr)
{
if(cnt[i]!=-1)
{
cnt[i]+=v;
sum[i] = (cnt[i]? (X[r+1]-X[l]):0);
return ;
}
}
PushDown(i,l,r);
int m=(l+r)/2;
if(ql<=m) update(ql,qr,v,lson);
if(m<qr) update(ql,qr,v,rson);
PushUp(i,l,r);
}
int bin(double key,int n,double d[])
{
int l=1,r=n;
while(r>=l)
{
int m=(r+l)/2;
if(d[m]==key)
return m;
else if(d[m]>key)
r=m-1;
else
l=m+1;
}
return -1;
}
int main()
{
int q;
int kase=0;
while(scanf("%d",&q)==1&&q)
{
int n=0,m=0;
for(int i=1;i<=q;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
X[++n]=x1;
nodes[++m]=node(x1,x2,y1,1);
X[++n]=x2;
nodes[++m]=node(x1,x2,y2,-1);
}
sort(X+1,X+n+1);
sort(nodes+1,nodes+m+1);
int k=1;//共k个不同的x坐标,组成了k-1个不同的区域
for(int i=2;i<=n;i++)
if(X[i]!=X[i-1]) X[++k]=X[i];
build(1,1,k-1);//少了build就WA
double ret=0.0;//最终面积
for(int i=1;i<m;i++)
{
int l=bin(nodes[i].l,k,X);
int r=bin(nodes[i].r,k,X)-1;
if(l<=r) update(l,r,nodes[i].d,root);
ret += sum[1]*(nodes[i+1].h-nodes[i].h);
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n",++kase,ret );
}
}