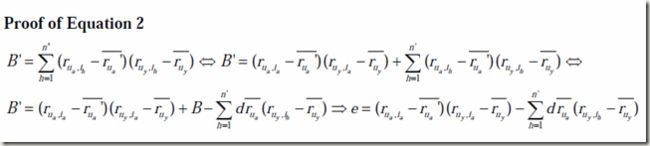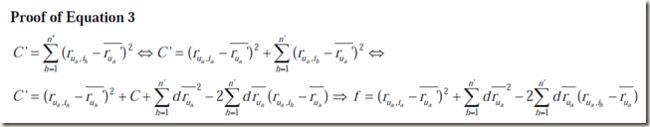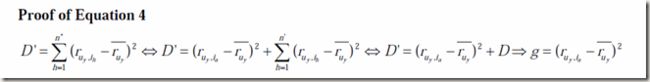基于增量更新的协同过滤

转载自：http://blog.sina.com.cn/s/blog_68ffc7a40100uec0.html

前面的一篇文章分析了基本的协同过滤算法，协同过滤最大的问题是计算量过大，为了解决这个问题，就有了基于增量更新的协同过滤方法。

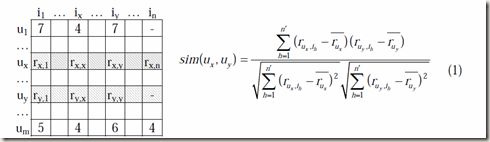
先回顾一下基本的协同过滤算法，计算两个用户基于显式评级的相似度公式如下：

那么我们有下面的公式：

需要解释一下，n'表示的是ux和uy共同评级的商品的个数。而，表示的用户ux，uy所有评级过商品的平均评级，需要注意的是这个平均评级是针对用户的所有评级商品的个数，不只是ux和uy的共同评级过的商品的个数。

那么如果系统中的评级发生了更新，新的相似度计算就有下面的公式：

由于B,C,D是旧有的，是已知的，那么我们的目标就是计算e，f，g，我们称之为增量，如果这些增量能够计算出来，那么基于已知的B，C，D，我们就很容易算出新的相似度。由于e，f，g的计算量相对较小，从而降低了算法复杂度，这就是增量更新算法的精髓。

下面就分析一下如何计算这些增量e，f，g。当系统中发生评级更新时，有这么两种情况：

1.用户提交一个新的商品的评级

计算用户ua和uy的相似度，用户ua对新的商品ia提交了一个新的评级，此时我们需要区分这么两种情况：

i uy已经对该商品ia进行了评级：在此情况下，B，C，D都需要更新。为什么呢？应为ua提交了新的评级，这会影响ua的平均评级，B，C的公式中都有ua的平均评级这个因子，因此B，C需要重新计算。至于D，由于在更新前，ua没有ia的评级，因此ia在相似度计算时被认为是一个无关的商品（因为两个人只有一个人对其进行了评级，从而无法比较），n'此时不包含ia的评级。但在更新之后，情况发生了变化，ua和uy对ia都有评级了，ia不再无关了，因此n'发生了变化。所以说D也需要更新。

ii uy没有对商品ia进行了评级：在此情况下，由于ia一直不是共同评级的商品，因此n'不会发生变化。由于n'没有变化，uy的平均评级又没有变化，那么D就没有变化，不需要更新。而ia的评级的加入会导致ua平均评级的变化，所以包含ua平均评级的因子的B，C也会发生更新。

2.用户更新了一个已经评级过的商品的评级

同上，我们也要区分这两种情况：

i uy已经评价了该更新的商品。在此情况下，B，C发生更新，因为ua的平均评级发生了变化，B，C包含了该因子。D不需要更新，因为n'，uy平均评级木有变化。

ii uy没有评级该更新的商品。此情况下，B，C发生了更新，D不更新。理由同上。

现在我们来考虑下在这么4种情况下，e,f,g等于什么，请看下表：

直接看结果可能大家可能不是很明白，用笔算一下就明白了，推导公式如下：

这里的表示的是ua更新前后评级之差

上面的推算比较简单，用笔在纸上划一下很容易得出上面的结果。

根据table 1的结果，我们看到，在4种情况下，e,f,g的公式实际上包含一些共同的因子，仔细研究一下这些因子，又可以发现这些因子又依赖于更加通用的一些因子。这些更加通用的因子就是需要我们在每次更新时缓存的数据。这样我们就可以利用这些缓存数据，用很低的计算复杂度计算出e,f,g，从而得出更新后的B',C',D'。

总结下，增量更新的本质在于对增量通过公式变换，发现增量依赖的因子，再进一步分析这些因子，从而发现这些因子可以通过哪些更加本质的因子计算出来，从而在每次更新计算中缓存的这些本质因子。算法复杂度降低的本质原因在于，增量的计算可以通过这些缓存的本质因子以较低的计算开销通过公式算出，通过公式发现这个计算开销只是一个线性乘加。

计算开销的一点分析

这种增量更新的算法数据库中每更新一条记录，都会引起一个增量更新计算，这个基本的增量更新计算开销我们用c表示, 从公式很容易看出，这个开销是o(1)，那么如果我们的更新计算是通过一个间隔为30分钟的后台进程来实现的话，如果30分钟包含了m个数据库记录更改，那么每次更新的开销为m*c，只有发生了更新的用户对才会产生计算开销.

而传统的协同过滤每过30分钟总是整个重新计算每两个用户的之间的相似度，而每个相似度的计算复杂度都是O（n）(n是共同评价的商品个数)。

所以算法性能高低，一目了然。在m<<n的情况下，性能的提高是很可观的。

协同过滤的一些变化

实际系统中的增量协同过滤，还有一些另外的思路和变化。相似度的衡量也有用杰卡德系数的。所谓杰卡德系数，就是交集除以并集，这个很好理解。对于本文中的例子，我们可以认为如果对同一件商品，用户ua和ub给出了相近的评级（比如评级分差小于一个阈值，比如1），那么认为这个商品是两个用户的交集。那么相似度就可以表示为:

sim(ua,ub)=ua对交集商品的评级和 + ub对交集商品的评级和/ua对所有商品的评级和+ub对所有商品的评级和 - ua对交集商品的评级和 - ub对交集商品的评级和

增量更新其实是一种思路，而不仅仅是一种算法，它可以用在很多方面。比如在杰卡德系数的体系中，系统每隔一定的时间间隔就更新两两之间的用户相似度，那么最直接的算法需要计算从时间原点到现在时间内发生的所有item的交集啊，并集啊什么的。如果采用增量更新的思路，我们其实不用计算这么多的item。我们把这些item区分成上次更新之前的item集合group-old，和上次更新时间距离这次更新时间之间的item集合group-new，那么通过集合变化和系统中上一次缓存的数据，我们可以把计算简化成类似求group-old , group-new之间的并集，交集操作，这就大大降低了复杂度，因为我们不用求所有item的交，并集，而只用求很小一部分item集合之间的并，交集操作。请看下面的公式，你也许很容易了解其中的秘密：

z = Items-all(a) ^ Items-all(b) = ( Items-old(a) + Items-new(a) )^( Items-old(b) + Items-new(b) )

= Items-old(a) ^ Items-old(b) + Items-old(a) ^ Items-new(b) + Items-new(a) ^ Items-old(b) + Items-new(a) ^ Items-new(b)

= z' + Items-old(a) ^ Items-new(b) + Items-new(a) ^ Items-old(b) + Items-new(a) ^ Items-new(b)

Items-old(a)表示用户a在更新之前的item集合

Items-old(b)表示用户b在更新之前的item集合

Items-new(b) 表示用户b从上次更新时间到这次更新时间之间产生的item的集合

Items-new(a) 表示用户b从上次更新时间到这次更新时间之间产生的item的集合

考虑到在大多数情况下，用户的Items-new(b)，Items-new(a)往往是0或者非常小，这种计算复杂度得降低可以想见。

[参考文献]

[1] Incremental Collaborative Filtering for Highly-Scalable Recommendation Algorithms