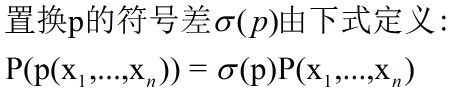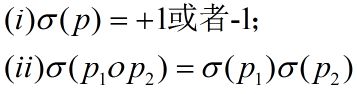线性代数(二十一) : 定义矩阵的行列式-介绍置换与群的概念

本节为行列式函数的定义做准备，介绍置换以及与之相关的群的概念

1 置换的概念

一个置换是n个对象(比如1,2,...,n)到自身的映射p,置换的性质如下：

(i) 置换像其他函数一样，可以进行复合。

(ii)置换是到上的 ，也就是说置换是满射

(iii)置换是单射

(iv)综合(ii)和(iii)置换是可逆的

综上性质,置换构成一个群，称为置换群。并且如果n不等于2这些群都是非交换群。

补充说明几个概念(不用深入理解)：

(1) 群：在数学中，群是一种代数结构，由一个集合G以及一个二元运算所组成。

如他们满足如下性质则可称为群(群公理):

(i) 封闭性。 对于所有G中a, b，运算a·b的结果也在G中。

(ii)结合性。 对于所有G中的a, b和c，等式 (a·b)·c = a· (b·c)成立。

(iii)单位元。 存在G中的一个元素e，使得对于所有G中的元素a，等式e·a = a·e = a成立。

(iv)反元素。 对于每个G中的a，存在G中的一个元素b使得a·b = b·a = e，这里的e是单位元。(也就是逆元，说明群的二元运算具有可逆性)

(2)交换群与非交换群

交换群也叫阿贝尔群，每一个群对应于一个集合和一个运算，如果这个运算满足交换律，则称为交换群。

2 置换的例子

置换为一个映射，并且是单射满射因此是可逆的。下边是一个置换的例子:

3 置换的判别式

设x1,x2,...,xn是n个变量，其判别式定义为：

4 定义置换的符号差

置换的符号差满足以下性质：

5 一类特殊的置换—对换