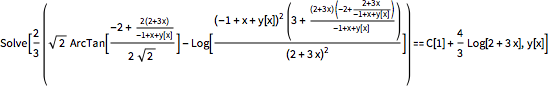微分方程的分类
转载：http://reference.wolfram.com/mathematica/tutorial/DSolveClassificationOfDifferentialEquations.html
微分方程的分类
虽然微分方程有三种基本类型——常微分方程（ODE）、偏微分方程（PDE）或者微分-代数方程（DAE），它们还可以进一步使用一些属性描述，如阶数（order）、线性性（linearity）和次数（degree）.
DSolve 所使用的解法和解的性质取决于要求解的方程类别.
一个微分方程的
阶数 是方程中导数的最高次数.
由于导数的最高阶数为1，所以这是一个一阶常微分方程.
| In[1]:= |
|
| Out[1]= |  |
这是一个四阶常微分方程的通解.
| In[2]:= |
|
| Out[2]= |
一个微分方程是线性的，如果方程关于
及其导数是一次的，并且如果系数是自变量的函数.
这是一个非线性二阶常微分方程，它表示一个循环摆的运动. 它是非线性的，因为
Sin
不是
的线性函数. 出现警告消息
，是因为
Solve 使用
JacobiAmplitude（
EllipticF 的逆）来寻找
的一个表达式.
的一个表达式.
| In[3]:= |
|
| Out[3]= |
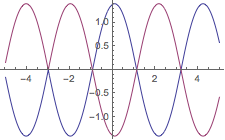
这里画出解的图形. 图中
处的不连续性由
Solve 使用的反函数的选择得到.
| In[4]:= |
|
| Out[4]= |  |
应当指出，有时候很简单的非线性方程的解仅以隐式提供. 在这种情况下，
DSolve 返回一个未计算的
Solve 对象.
这种非线性微分方程只有一个隐式的解.
提示信息可以忽略；它们的出现是由于
Solve 找不到
的显式表达式，因为涉及到了非代数函数（
ArcTan 和
Log）.
| In[5]:= |
|
| Out[5]= |  |
当一个线性常微分方程的系数不依赖于
时，则称该常微分方程具有
常系数.
这是一个具有常系数的常微分方程.
| In[6]:= |
|
| Out[6]= |  |
前面的方程也是
齐次 的：所有的项都包含
或者
的导数，而它的右边是0. 增加一个自变量的函数使得方程成为
非齐次 的. 一个具有常系数的非齐次方程的通解可以由对相应的齐次方程的解加入一个特定的积分得到.
这里，对于前面的方程的右边加入
，使得新方程成为非齐次的. 该新方程的通解是前面的解和一个特定积分的和.
| In[7]:= |
|
| Out[7]= |
当一个常微分方程的系数取决于
时，则称该常微分方程具有
变系数. 由于具有变系数为
的有理函数的方程具有容易分类的奇点，所以我们具有求解它们的一些更精巧的算法.
该方程的系数是
的有理函数.
| In[8]:= |
|
| Out[8]= |  |
在函数和微分方程之间存在密切关系. 从一个任意类型的函数开始，可以构造一个满足该函数的微分方程. 反之，任意微分方程产生一个或者多个函数，以该方程的解的形式给出. 事实上，许多经典分析中的特殊函数源于微分方程的解.
Mathieu 函数 就是这类特殊函数的一种. Mathieu 对椭圆模振动的研究感兴趣. 描述这种运动的波动方程的本征函数由 Mathieu 函数的积给出.
这种具有有理系数的线性二阶常微分方程具有由马蒂厄（Mathieu）函数给出的通解.
| In[9]:= |
|
| Out[9]= |  |
在前面的解中
ArcCos
[t] 的出现表明方程可以使用三角函数给出一个更简单的形式. 这是 Mathieu 在1868年推出的方程的形式.
| In[10]:= |
|
| Out[10]= |  |
这里画出给方程的解的特定的积的表面图.
| In[11]:= |
|
| Out[11]= |
一个微分方程的
次数 是方程的最高阶导数的最高幂（highest power）.
这是一个次数为2的一阶常微分方程.
| In[12]:= |
|
| Out[12]= |  |
较高的次数导致解的非唯一性.
| In[13]:= |
|
| Out[13]= |
本教程中的例子集中在常微分方程的分类. 偏微分方程的分类类似，但是更加复杂. 偏微分方程也可以根据线性或者非线性、阶数、次数和常系数或变系数归类. 更加重要的是识别偏微分方程为双曲型、抛物型或者椭圆形的分类法. 这些分类在 "二阶偏微分方程" 中有进一步的详细讨论.