HDU1030数学之美

Delta-wave

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4656    Accepted Submission(s): 1762

Problem Description

A triangle field is numbered with successive integers in the way shown on the picture below. 



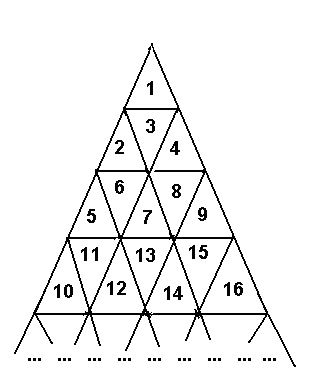
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route. 

Write the program to determine the length of the shortest route connecting cells with numbers N and M. 

 

Input

Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).

 

Output

Output should contain the length of the shortest route.

 

Sample Input

   
   
   
   

    
    
    
    6 12 
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    3
   
   
   
   

 

Source

Ural Collegiate Programming Contest 1998

 

Recommend

lcy

 

思路：这种题目第一次见，蛮有意思的，用的是找规律的办法．其中每一个点都有一个三维坐标(level,l,r).其中level表示水平坐标，l表示左斜45度坐标，r表示右斜45度坐标．我们只需要将两个点的三维坐标对应绝对值之和，就是题目所要求的最短路径．重点在于三维坐标的求法．

规律是：第1层有1个数，第2层有3个数，第3层有5个数，．．．．第i层有2i-1个数

现在我们知道了一个数n,满足1+3+5+......(2i-1)+x=n,i即为水平坐标．现在我们需要编程实现这个功能求i.

项数递推式：

Ai=A(i-1)+2,A1=1;

Sum=Sum+Ai;Sum=0;

循环就可以找到水平坐标，l,r坐标还是看代码吧．

//找规律的题目
#include <iostream>
#include<cmath>
using namespace std;
int abs(int a)
{
	return a>0?a:-a;
}
void Set(int n,int& level,int& left,int& right)
{
	int i,sum=0,count=1;
	//1 3 5 7....
	for( i=1 ; sum + i<n ; i += 2 )
	{
		sum += i;
		++count;
	}
	//此时的sum表示的是上面所有层的元素总数,i表示下一层的元素个数
	level = count; 
	left = (n-sum+1)/2; 
	right = (sum+i-n)/2+1;
}
int main()
{
	int n,m,level1,l1,r1,level2,l2,r2;
	/*while(cin>>n)
	{
		Set(n,level1,l1,r1);
		cout<<n<<' '<<level1<<' '<<l1<<' '<<r1<<endl;
	}*/
	while(cin>>n>>m)
	{
		Set(n,level1,l1,r1);
		Set(m,level2,l2,r2);
		cout<<abs(level1-level2)+abs(l1-l2)+abs(r1-r2)<<endl;
	}

}