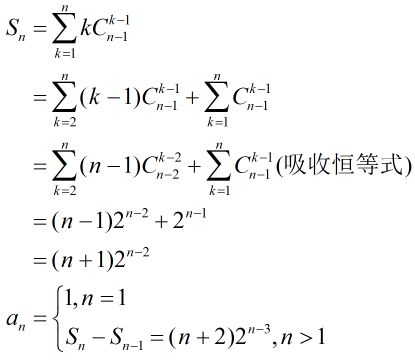HDU 4602 Partition (整数拆分&找规律&快速幂取模)
Partition
http://acm.hdu.edu.cn/showproblem.php?pid=4602
Memory Limit: 32768/32768 K (Java/Others)
Problem Description
Define f(n) as the number of ways to perform n in format of the sum of some positive integers. For instance, when n=4, we have
4=1+1+1+1
4=1+1+2
4=1+2+1
4=2+1+1
4=1+3
4=2+2
4=3+1
4=4
totally 8 ways. Actually, we will have f(n)=2 (n-1) after observations.
Given a pair of integers n and k, your task is to figure out how many times that the integer k occurs in such 2 (n-1) ways. In the example above, number 1 occurs for 12 times, while number 4 only occurs once.
4=1+1+1+1
4=1+1+2
4=1+2+1
4=2+1+1
4=1+3
4=2+2
4=3+1
4=4
totally 8 ways. Actually, we will have f(n)=2 (n-1) after observations.
Given a pair of integers n and k, your task is to figure out how many times that the integer k occurs in such 2 (n-1) ways. In the example above, number 1 occurs for 12 times, while number 4 only occurs once.
Input
The first line contains a single integer T(1≤T≤10000), indicating the number of test cases.
Each test case contains two integers n and k(1≤n,k≤10 9).
Each test case contains two integers n and k(1≤n,k≤10 9).
Output
Output the required answer modulo 10
9+7 for each test case, one per line.
Sample Input
2 4 2 5 5
Sample Output
5 1
1. 观察发现n的分拆中n出现了1次,n-1出现了2次,n-2出现了5次,……,这一发现是否正确?
这样想:n出现了1次不用说;n-1出现了2次是因为剩下那个数是1,它只能和n-1有两种组合,或者当n=2时变成1+1,那也有2个数;n-2出现了5次是因为剩下的数2可以与n-2有3+2种组合,……
那么,记a1=1,a2=2,a3=5,...,我们的目标就是求出an。
2. 如何求出an?
利用公式:an=Sn-Sn-1
3. 如何求出Sn?
考虑将n分成k个正数,由插空法知有C(n-1,k-1)种分法(或者:这等价于方程x1+x2+...+xk = n-k的非负解的个数,亦等价于从k种不同的物品中允许重复地选出n-k个物品的方法数),于是求出总个数Sn:
4. 注意n,k可能较大,要使用快速幂取模。
完整代码:
/*31ms,228KB*/
#include<cstdio>
const int mod = 1000000007;
__int64 pow(__int64 a, __int64 b)///a^b % mod
{
__int64 r = 1, base = a;
while (b)
{
if (b & 1)
r = r * base % mod;
base = base * base % mod;
b >>= 1;
}
return r;
}
int main()
{
int t;
scanf("%d", &t);
while (t--)
{
int n, k;
scanf("%d%d", &n, &k);
if (k > n)
puts("0");
else
{
int temp = n + 1 - k;
if (temp == 1)
puts("1");
else if (temp == 2)
puts("2");
else
printf("%I64d\n", (temp + 2) * pow(2, temp - 3) % mod) ;
}
}
return 0;
}