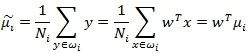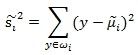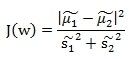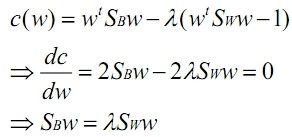特征变换以及维度下降——Linear Discriminant Analysis(一)
1.LDA概述
线性判别分析(Linear discriminant analysis, LDA),是一种监督学习算法,也叫做Fisher线性判别(Fisher Linear Discriminant, FLD),是模式识别的经典算法,它是在1996年由Belhumeur引入模式识别和人工智能领域的。线性判别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间有最佳的可分离性。因此,它是一种有效的特征提取方法。
2.LDA原理
LDA的原理是,将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近。
3.Linear discriminant analysis(二类情况)
给定N个d维的样本(i从1到N),其中,有N1个样例属于类别W1,有N2个样例属于类别W2(N1+N2=N)。现在我们觉得原始特征数太多,想将d维特征降到只有一维,而又能保证类别能够“清晰”地反映在低维数据上,也就这一维就能决定每个样例的类别。降维函数(或者叫投影函数)是![]() (x为d维,w为d维)最后我们就根据每个样例的y值来判断它属于哪一类。这里的y值如果只考虑二值分类的情况,y=1或y=0,而y值又是x投影到直线上的点到原点的距离。
(x为d维,w为d维)最后我们就根据每个样例的y值来判断它属于哪一类。这里的y值如果只考虑二值分类的情况,y=1或y=0,而y值又是x投影到直线上的点到原点的距离。
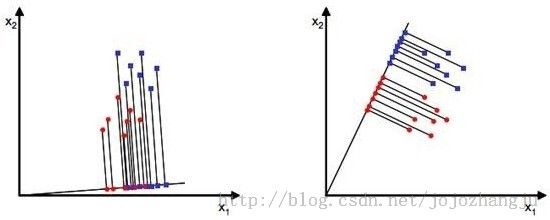
如,当x是二维的,我们就要找到一条直线来做投影,然后寻找最能使样本点分离的直线。
显然,从直观上看,右图的效果比较好,可以很好的将不同类别的样本点分离。
下面,我们就要找到这个最佳的w,使得样例映射到y后最易于区分。
首先,我们寻找每类样例的均值(中心点),这里只有两类。
由于x到w投影后的样本点均值为:
由此可知,投影后的均值也就是样本中心点的投影。
所谓最佳直线或是最佳的方向(w),就是能够使投影后的两类样本的中心点尽量分离的直线。
![]() (3)
(3)
所以我们希望,J(w)越大越好。
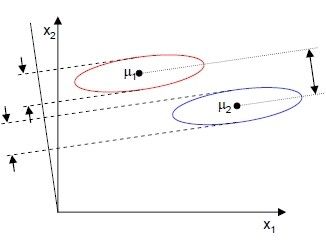
但是单纯考虑J(w)是不行的,因为:
图中,样本点分布在两个不同颜色的椭圆里,投影到横轴x1可以获得最大的中心点间距,但是由于有所重叠,x1不能分离样本点。投影到纵轴x2上,虽然样本点中心间距较小,但是能够分离样本点。因此,我们还需要考虑样本点投影后的内部方差,方差越小越好。
我们使用另外一个度量值,称作散列值(scatter)。
上式子其实就是一个少除以样本数量的方差值,散列值的几何意义是样本点的密集程度,值越大,越分散,值越小,越集中。
而我们想要的投影后的样本点的样子是:不同累呗的样本点越分开越好,同类的越聚集越好,也就是均值差越大越好,散列值越小越好。所以,我们使用J(w)以及S来度量,最终度量公式为:
所以我们只需要J(w)最大。
我们把散列值公式展开:
(6)
然后我们定义上式中间的部分:
上式的就是少除以样本数的协方差矩阵,称为散列矩阵(scatter matrices)
下面:
![]() (8)
(8)
Sw称为类内散列矩阵(within-class scatter matrix)
然后我们回到(6)式中,使用(7)替换中间部分,得到:
(9)
然后展开式子:
(10)
SB称为类间散列矩阵(between-class scatter matrix),是两个向量的内积,虽然是个矩阵,但是秩为1。
最终的J(w)表示为:
在我们求导之前,需要对分母进行归一化,因为不做归一的话,w扩大任何倍,都成立,我们就无法确定w。因此我们打算令![]() ,那么加入拉格朗日乘子后,求导:
,那么加入拉格朗日乘子后,求导:
其中用到了矩阵微积分,求导时可以简单地把当做对待。
如果Sw可逆,得:
(13)
所以,w就是的特征向量了。
这个公式称为Fisher linear discrimination。
另外,W也可以通过以下方式求出:
![]() (14)
(14)
至此,我们只需要求出原始样本的均值和方差就可以求出最佳的方向w,这就是Fisher于1936年提出的线性判别分析。
所以上面二维样本的投影结果图为:
之后我们会继续介绍多类的情况。