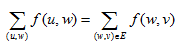poj 2396(有源汇的上下界可行流。。。。。dinic)
上下流相关的网络流的各种问题在Amber大牛的《图论原理》里讲的特备清楚。。。。。资料需要网上下载。。我就把原文摘抄下来吧。。。。。。
问题模型:
给定一个加权的有向图,满足:
(1)容量限制条件:
(2)流量平衡条件:
(2)中的即除了源汇外,所有点都满足流量平衡条件,则称G为有源汇网络;否则![]() ,即不存在源汇,所有点都满足流量平衡条件,则称G为无源汇网络。
,即不存在源汇,所有点都满足流量平衡条件,则称G为无源汇网络。
将这类问题由易到难一一解决:
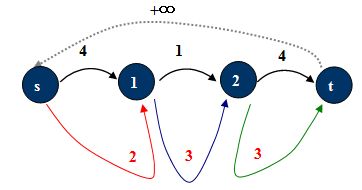
问题[1] 求无源汇的网络有上下界的可行流
由于下界是一条弧上的流必需要满足的确定值。下面引入必要弧的概念:必要弧是一定流要满的弧。必要弧的构造,将容量下界的限制分离开了,从而构造了一个没有下界的网络G’:
由于必要弧的有一定要满的限制,将必要弧“拉”出来集中考虑:
添加附加源x, 附加汇y。想像一条不限上界的(y, x),用必要弧将它们“串”起来,即对于有向必要弧(u, v),添加(u, y),(x, v),容量为必要弧容量。这样就建立了一个等价的网络。
一个无源汇网络的可行流的方案一定是必要弧是满的。若去掉(y, x)后,附加源x到附加汇y的最大流,能使得x的出弧或者y的入弧都满,充要于原图有可行流。
算法:
1. 按上述方法构造新网络(分离必要弧,附加源汇)
2. 求附加源x到附加汇y的最大流
3. 若x的出弧或y的入弧都满,则有解,将必要弧合并回原图;否则,无解。
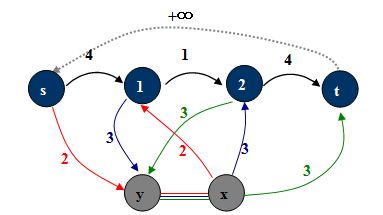
问题[2] 求有源汇的网络有上下界的可行流
加入边(t, s),下界为0(保证不会连上附加源汇x, y),不限上界,将问题[2]转化为问题[1]来求解。
问题[3]求有源汇的网络有上下界的最大流
算法:
1. 先转化为问题[2]来求解一个可行流。若可行无解,则退出。由于必要弧是分离出来的,所以就可以把必要弧(附加源汇及其临边)及其上的流,暂时删去。再将(T,S)删去,恢复源汇。
2. 再次,从S到T找增广轨,求最大流。
3. 最后将暂时删去的下界信息恢复,合并到当前图中。输出解。
这样既不破坏下界(分离出来)也不超出上界(第2步满足容量限制),问题解决。
问题[4]求有源汇的网络有上下界的最小流
算法:
1. 同问题[3]。
2. 从T到S找增广轨,不断反着改进。
3. 同问题[3]。
问题[3]与问题[4]的另一种简易求法:
注意问题[2]中,构造出的(t, s),上下界几乎没什么限制。下面看看它的性质:
定理:如果从s到t有一个流量为a的可行流f,那么从t到s连一条弧(t, s),其流量下界b(t, s) = a,则这个图一定有一个无源汇的可行流:除了弧(t, s)的容量为a外,其余边的容量与f相同。
证明:如果从s到t的最大流量为amax,那么从t到s连一条下界b(t, s) = a’ > amax的弧(t, s),则从在这个改造后的图中一定没有无源汇的可行流:否则将这个可行流中的弧(t, s)除去,就得到了原图中s到t的流量为a’的流,大于最大流量amax,产生矛盾。
可以二分枚举这个参数a,即下界b(t, s),每次用问题[1]判断是否有可行流。这样就可以求出最大流。
同理,问题[4]要求最小流,只要二分枚举上界c(t, s)即可。
因为朴素的预流推进算法O(N3),总复杂度为O(N3 log2流量) 。
思路:
无源汇 (附加源汇+最大解决)
有源汇 (附加(T,S)->无源汇)
根据这个讲解自己写一个相应的程序就可以了。。。这个题里面。。把每一行看成一个点。。每一列看成一个点来建图。。。。(IMPOSSIBLE少写一个s wa了半天。。挥泪呀。。。。TT。。。)
还有就是网上的上下界的网络流之类的的题不是很多。。。建议好好刷每一道题。。。。。
( 在给一个小小的OJ bug就是虽然说每两个case间输出空行。。其实不要理会。。。每个case都输出也会是对的。。。。OJ不会去判最后的那一行有没有空行。。。。不过只试用于现阶段呀。。。有一次校赛。。就专门卡这个。。还提示wa。。。可想而知当时的结果。。。。。)
| Time Limit: 3000MS | Memory Limit: 65536K | |||
| Total Submissions: 3469 | Accepted: 1313 | Special Judge | ||
Description
And, by the way, no one really reads budget proposals anyway, so we'll just have to make sure that it sums up properly and meets all constraints.
Input
Each constraint consists of two integers r and q, specifying some entry (or entries) in the matrix (the upper left corner is 1 1 and 0 is interpreted as "ALL", i.e. 4 0 means all entries on the fourth row and 0 0 means the entire matrix), one element from the set {<, =, >} and one integer v, with the obvious interpretation. For instance, the constraint 1 2 > 5 means that the cell in the 1st row and 2nd column must have an entry strictly greater than 5, and the constraint 4 0 = 3 means that all elements in the fourth row should be equal to 3.
Output
Sample Input
2 2 3 8 10 5 6 7 4 0 2 > 2 2 1 = 3 2 3 > 2 2 3 < 5 2 2 4 5 6 7 1 1 1 > 10
Sample Output
2 3 3 3 3 4 IMPOSSIBLE
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=300;
const int INF=0x7fffffff;
int n,m,test,s,t,S,T,N;
int in[MAXN],out[MAXN];
int num[MAXN],h[MAXN],c[MAXN][MAXN],f[MAXN][MAXN];
int up[MAXN][MAXN],low[MAXN][MAXN],row[MAXN],col[MAXN];
void Init()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;++i)
scanf("%d",&row[i]);
for (int i=1;i<=m;++i)
scanf("%d",&col[i]);
for (int i=1;i<=n;++i)
for (int j=1;j<=m;++j)
up[i][j+n]=INF;
int temp,x,y,z;
char ch;
scanf("%d",&temp);
while (temp--)
{
scanf("%d %d %c %d",&x,&y,&ch,&z);
//printf("%d %d %c %d\n",x,y,ch,z);
if (x!=0 && y==0)
for (int i=1;i<=m;++i)
{
if (ch=='=') up[x][i+n]=low[x][i+n]=z;
if (ch=='<') up[x][i+n]=min(up[x][i+n],z-1);
if (ch=='>') low[x][i+n]=max(low[x][i+n],z+1);
}
if (x==0 && y!=0)
for (int i=1;i<=n;++i)
{
if (ch=='=') up[i][y+n]=low[i][y+n]=z;
if (ch=='<') up[i][y+n]=min(up[i][y+n],z-1);
if (ch=='>') low[i][y+n]=max(low[i][y+n],z+1);
}
if (x==0 && y==0)
for (int i=1;i<=n;++i)
for (int j=1;j<=m;++j)
{
if (ch=='=') up[i][j+n]=low[i][j+n]=z;
if (ch=='<') up[i][j+n]=min(up[i][j+n],z-1);
if (ch=='>') low[i][j+n]=max(low[i][j+n],z+1);
}
if (x!=0 && y!=0)
{
if (ch=='=') up[x][y+n]=low[x][y+n]=z;
if (ch=='<') up[x][y+n]=min(up[x][y+n],z-1);
if (ch=='>') low[x][y+n]=max(low[x][y+n],z+1);
}
}
s=0,t=n+m+1;
for (int i=1;i<=n;++i)
low[s][i]=up[s][i]=row[i];
for (int i=1;i<=m;++i)
low[i+n][t]=up[i+n][t]=col[i];
/*for (int i=1;i<=n;++i)
for (int j=1;j<=m;++j)
printf("%d %d %d %d\n",i,j,up[i][j+n],low[i][j+n]);*/
}
int Find(int u,int flow)
{
if (u==T) return flow;
int temp=flow,pos=N-1;
for (int i=0;i<N;++i)
{
if (h[u]==h[i]+1 && c[u][i]>0)
{
int F=Find(i,min(temp,c[u][i]));
c[u][i]-=F,c[i][u]+=F;
f[u][i]+=F,f[i][u]-=F;
temp-=F;
if (temp==0 || h[S]==N) return flow-temp;
}
if (c[u][i]>0 && h[i]<pos) pos=h[i];
}
if (temp==flow)
{
--num[h[u]];
if (num[h[u]]==0) h[S]=N;
else
{
h[u]=pos+1;
++num[h[u]];
}
}
return flow-temp;
}
int SAP()
{
int sum=0;
memset(h,0,sizeof(h));
memset(num,0,sizeof(num));
num[0]=N;
while (h[S]<N) sum+=Find(S,INF);//,printf("%d\n",sum);
return sum;
}
void Solve(int s,int t,int tot)
{
S=tot,T=tot+1;
int tflow=0;
for (int i=0;i<tot;++i)
for (int j=0;j<tot;++j)
{
c[i][j]=up[i][j]-low[i][j];
in[j]+=low[i][j];
out[i]+=low[i][j];
tflow+=low[i][j];
}
for (int i=0;i<tot;++i)
{
c[S][i]=in[i];
c[i][T]=out[i];
}
c[t][s]=INF;
N=tot+2;
/*&for (int i=0;i<N;++i)
for (int j=0;j<N;++j)
printf("%d %d %d\n",i,j,c[i][j]);*/
int ans=SAP();
//printf("%d %d\n",ans,tflow);
if (ans!=tflow) {printf("IMPOSSIBLE\n");return;}
c[s][t]=c[t][s]=0;
SAP();
for (int i=1;i<=n;++i)
{
for (int j=1;j<=m;++j)
printf("%d ",f[i][j+n]+low[i][j+n]);
printf("\n");
}
}
void Perpare()
{
memset(in,0,sizeof(in));
memset(out,0,sizeof(out));
memset(c,0,sizeof(c));
memset(f,0,sizeof(f));
memset(up,0,sizeof(up));
memset(low,0,sizeof(low));
}
int main()
{
freopen("in","r",stdin);
freopen("out","w",stdout);
scanf("%d",&test);
while (test--)
{
Perpare();
Init();
Solve(s,t,n+m+2);
printf("\n");
}
return 0;
}