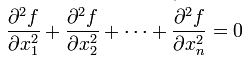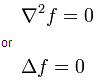- Node.js-fs模块
会飞的鱼先生
node.jsvim编辑器
文件写入异步写入文件(fs.writeFile())//语法:fs.writeFile(file,data[,options],callback)//参数:文件路径、数据、选项(可选)、回调函数(err)constfs=require('fs');fs.writeFile('file.txt','HelloNode.js',function(err){if(err)throwerr;console
- 探索高效缓存:CoroutinesCache 开源库深度解析
龙香令Beatrice
探索高效缓存:CoroutinesCache开源库深度解析CoroutinesCacheInmobiledevelopmentexistssolutionforcachingwithRxJavausage,butthereisnosolutionsforKotlinCoroutines.Theprojectistoprovidethisfunctionalitytomobilecommunity.
- GO 语言学习 之 函数
唯独不开心
golang学习go开发语言
函数我们一直都在使用,但是还是有很多细节的内容需要深入了解一下,方便后续的编码实践。函数定义:func函数名([参数列表])[返回值]{函数体}funcadd(aint,bint)int{returna+b}基本概念:函数签名(FunctionSignature):包含函数名、参数列表(参数的类型和顺序)以及返回值类型。在示例中add(aint,bint)int就是函数签名。它定义了函数的外部接口
- Definition of a Requirement
workflower
软件需求软件工程需求分析敏捷流程开发语言
IEEE给出的需求定义Firstofall,whatismeantbyarequirement?HereisatypicaldefinitiondrawnfromIEEE-STD-1220-1998(IEEE1998):Requirement:astatementthatidentifiesaproductorprocessoperational,functional,ordesigncharac
- React Error Boundary
Happy_Ariel
react.jsjavascript前端
ReactErrorBoundaryimport*asReactfrom'react';import{Component}from'react';import{createRoot}from'react-dom/client';functionrenderWithError(){thrownewError('error');}functionA(){return{renderWithError()
- SeaTunnel2.1.1源码解析
Adobee Chen
大数据知识点seaTunnel大数据
目录一:启动脚本解析二:源码解析入口2.execute()核心方法1.其中BaseSource、BaseTransform、BaseSink都是接口、都实现Plugin接口。他们的实现类就是对应的插件类型2.execute()方法向下走,创建一个执行环境。3.调用plugin.prepare(env)4.最后启动execution.start(sources,transforms,sinks);5
- 第 3 章:神经网络如何学习
鱼摆摆拜拜
神经网络学习人工智能
第3章:神经网络如何学习在第二章中,我们详细了解了神经网络的静态结构:由神经元组成的层,以及连接它们的权重和偏置。现在,我们将进入整个教程最核心的部分:神经网络是如何从数据中"学习"的?这个学习过程是一个动态的、不断调整自身参数以求更佳预测的过程。我们将通过四个关键概念来揭示这个秘密:前向传播(ForwardPropagation):数据如何通过网络产生一个预测?损失函数(LossFunction
- 机器学习中的数学:数学建模常用知识点-1
数字化与智能化
机器学习中的数学机器学习凸函数泰勒公式Jensen不等式
一、凸函数1、凸函数讲解设函数f(x)是定义在区间X上的函数,若对于区间上任意两点x1、x2和任意实数��∈(0,1),总有如下表达式成立:则称为f(x)是X上的凸函数;反之,如果下式成立:则称为f(x)在X上的凹函数。如图所示:Python实现凸函数:importnumpyasnpimportmatplotlib.pyplotasplt#定义凸函数defconvex_function(x):re
- 在C#中 属性(Properties)get 和 set
周杰伦fans
ai学习参考学习C#的笔记c#服务器
在C#中,属性(Properties)是一种特殊的方法,用于封装类、结构或接口中的字段。属性允许你控制对字段的访问,并可以在设置或获取值时执行额外的逻辑。属性通常由两个访问器组成:get和set。基本属性定义publicclassPerson{privatestringname;publicstringName{get{returnname;}set{name=value;}}}在这个例子中,Na
- 接口测试-第03天(Postman断言、关联、参数化)
粥小铭同学
接口测试postman测试工具
Postman断言Postman断言简介让Postman工具代替人工自动判断预期结果和实际结果是否一致断言代码书写在Tests标签页中。查看断言结果TestResults标签页Poatman常用断言1.断言响应状态码Statuscode:Codeis200//断言响应状态码为200pm.test("Statuscodeis200",function(){pm.response.to.hava.st
- 【通过 emit() 触发的自定义事件】
软件205
VUE3API前端javascript开发语言
@[TOC](通过emit()触发的自定义事件)子组件搜索重置constemit=defineEmits();.item-search{margin-left:12px;}父组件使用importFormSearchfrom"@/components/FormSearch/index.vue";consthandleQuery=()=>{console.log("搜索参数:",{...queryPa
- 虚幻引擎编程反射系统实现
污领巾
虚幻php游戏引擎
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言1、反射的核心实现流程1.1宏定义标记1.2UnrealHeaderTool(UHT)处理1.3生成的代码结构1.4运行时反射数据注册2、反射系统的关键数据结构2.1UClass2.2UProperty及其派生类2.3UFunction3、反射的实际应用场景3.1蓝图与C++交互3.2序列化与反序列化3.3网络同步(Rep
- DAY 42 Grad-CAM与Hook函数
@浙大疏锦行https://blog.csdn.net/weixin_45655710知识点回顾回调函数lambda函数hook函数的模块钩子和张量钩子Grad-CAM的示例作业:理解下今天的代码即可importtorchimporttorch.nnasnnimporttorch.nn.functionalasFimporttorchvisionimporttorchvision.transfor
- JavaScript 原型链继承中的引用类型陷阱
JavaScript原型链继承中的引用类型陷阱本文通过一个生动的案例,解析JavaScript原型链继承中引用类型属性的共享问题,帮助开发者理解原型链机制并避免常见陷阱。问题代码展示//父类构造函数functionAnimal(){this.skills=['eat','sleep'];//引用类型属性this.mouse=1;//基本类型属性this.name='Animal';this.sho
- SpringCloud-config配置中心
Enter_灵猴
每日一记
config服务端启动类要加@EnableConfigServerbootstrap.propertiesspring.application.name=config-serverserver.port=f服务端启动端口号spring.cloud.config.server.git.uri=https://github.com/登陆账号/仓库名spring.cloud.config.server.
- 通过 es6的标签模板字符串,调用函数
改了一个昵称
es6javascript
es6的标签模板字符串/***讲一下es6的标签模板字符串*/functionfoo(...args){console.log(args);//打印的是:['why',18,1.88]}`调用foo函数,方式一`//foo('why',18,1.88)`调用foo函数,方式二`letname='coder'letage=19//也可以这样调用foo函数foo`mynameis${name},age
- Error in created hook: “TypeError: Cannot read properties of undefined (reading ‘style‘)“
本郡主是喵
#JS相关vue.jsjavascript前端
问题解决这个错误通常在Vue组件的created钩子函数中发生,它表示在该钩子函数中尝试读取一个未定义的对象的style属性。造成这个错误的原因可能是:你在`created`钩子函数中引用了一个未定义的数据属性或计算属性。在`created`钩子函数中尝试访问组件的DOM元素,但DOM元素尚未完全加载或渲染。为了解决这个问题,你可以按照以下步骤进行排查:检查在created钩子函数中访问的数据属性
- PAT A 1043 Is It a Binary Search Tree
cwn_
算法c++数据结构图论
ABinarySearchTree(BST)isrecursivelydefinedasabinarytreewhichhasthefol‐lowingproperties:•Theleftsubtreeofanodecontainsonlynodeswithkeyslessthanthenode’skey.•Therightsubtreeofanodecontainsonlynodeswithk
- TS 函数泛型和泛型约束
邱志刚
TS前端
仅供参考,自己学习记笔记。//函数泛型functionAdd(a:T,b:T):Array{return[a,b]}Add(1,2);Add('1','2');//多个泛型functionSub(a:T,b:B):Array{return[a,b]}Sub(1,'aa')//泛型约束interfaceLen{length:Number}functiongetLength(arg:T){return
- TS泛型笔记
红中马喽
笔记
1.泛型基础概念定义:泛型是TypeScript中允许创建可复用组件的特性,这些组件可以支持多种数据类型,而非单一特定类型。核心优势:代码复用性:同一组件可处理不同类型数据类型安全:在编译阶段捕获类型错误灵活性:保持代码的灵活性同时提供强类型支持泛型函数//基础泛型函数语法functionidentity(arg:T):T{returnarg;}//使用方式constresult=identity
- day39
心落薄荷糖
Python训练营python
#先继续之前的代码importtorchimporttorch.nnasnnimporttorch.optimasoptimfromtorch.utils.dataimportDataLoader,Dataset#DataLoader是PyTorch中用于加载数据的工具fromtorchvisionimportdatasets,transforms#torchvision是一个用于计算机视觉的库,
- 钉钉小程序摸索二:钉钉小程序开发过程中错误解决过程
钉钉小程序开过程中作为小白,很容易遇上各种问题,今天我就以自己开发过程的遇到的问题总结下解决过程或者思路,有小白的同学可以做下参考,发布文章不易,请点赞一下鼓励下,谢谢。目录:TypeError:my.requestisnotafunctionatObject.onSubmit1、钉钉开发过程中接口请求返回TypeError:my.requestisnotafunctionatObject.onS
- 【.net core】【watercloud】【layui】弹出层回调方法定位当前弹出层位置并调用弹出窗口内部方法
MoFe1
.netcorelayui前端
common.modalOpen({title:"数据生成",url:"your/url/path",width:"95%",height:"90%",yes:function(index,layero){//定位到顶层窗口查找,如果仅使用window,为从当前页面窗口查找,会查找不到信息variframeWin=top.window[layero.find('iframe')[0]['name'
- js递归性能优化
啃火龙果的兔子
开发DEMOjavascript开发语言ecmascript
JavaScript递归性能优化递归是编程中强大的技术,但在JavaScript中如果不注意优化可能会导致性能问题甚至栈溢出。以下是几种优化递归性能的方法:1.尾调用优化(TailCallOptimization,TCO)ES6引入了尾调用优化,但只在严格模式下有效:'usestrict';//普通递归functionfactorial(n){if(n===1)return1;returnn*fa
- 右移的错误使用 造成 超出时间限制 解决方案
aPurpleBerry
LeetCode做题总结算法力扣二分查找
题目链接:https://leetcode.cn/problems/guess-number-higher-or-lower/?envType=study-plan-v2&envId=leetcode-75最开始的代码varguessNumber=function(n){letl=1,r=n;while(l>1;if(guess(m)===-1){r=m-1;}elseif(guess(m)===
- Spring Boot项目初始化加载自定义配置文件内容到静态属性字段
@Corgi
Java面试题springboot后端java
文章目录创建配置文件cXXX.properties配置类XXXConfig.java添加第三方JAR包创建配置文件cXXX.properties在resource目录下新建配置文件cXXX.properties,内容如下:#商户号mch_id=xxxxx#商户密码pwd=xxxx#接口请求地址req_url=https://xxx#异步回调通知地址(请替换为实际地址)notify_url=htt
- 三阶落地:腾讯云Serverless+Spring Cloud的微服务实战架构
大熊计算机
#腾讯云架构腾讯云serverless
云原生演进的关键挑战(1)传统微服务架构痛点资源利用率低(非峰值期资源闲置率>60%)运维复杂度高(需管理数百个容器实例)突发流量处理能力弱(扩容延迟导致P99延迟飙升)(2)Serverless的破局价值腾讯云SCF(ServerlessCloudFunction)提供:毫秒级计费粒度(成本下降40%~70%)百毫秒级弹性伸缩(支持每秒万级并发扩容)零基础设施运维同步调用异步事件用户请求API网
- 【开源项目】「安卓原生3D开源渲染引擎」:Sceneform‑EQR
「安卓原生3D开源渲染引擎」:Sceneform‑EQR渲染引擎“那一夜凌晨3点,第一次提交PR的手在抖……”——我深刻体会这种忐忑与激动。仓库地址:(github.com)。一、前言:开源对我意味着什么DIY的自由Vs.工业化的束缚刚入Android原生开发时,我习惯自己在项目里嵌入各种3D渲染/AR/XR模块,结构臃肿、流程混乱。当我知道GoogleSceneformSDK被弃用,起初只是出于
- JavaScript中的函数柯里化(Currying):从概念到实战
coding随想
JavaScriptjavascriptecmascript开发语言前端
JavaScript中的函数柯里化(Currying):从概念到实战在JavaScript开发中,函数式编程(FunctionalProgramming)逐渐成为一种主流思想。而函数柯里化(Currying),正是这一思想中的核心技巧之一。它不仅能提升代码的复用性和灵活性,还能帮助我们构建更优雅、更模块化的解决方案。本文将带你从零开始,深入理解柯里化的原理、实现方式及实际应用场景。一、什么是函数柯
- uniapp处理后端返回的html字符串
萌新咦~
uni-app
前言:采用v-html方法处理1.处理前↵↵document.forms[0].submit();2.处理后↵↵document.forms[0].submit();3.跳转页面方法//传参uni.setStorageSync("ICBC_GW_V3_HTML",res.result.payUrl)//跳转uni.navigateTo({url:"/subpages/cashier/webView
- ASM系列四 利用Method 组件动态注入方法逻辑
lijingyao8206
字节码技术jvmAOP动态代理ASM
这篇继续结合例子来深入了解下Method组件动态变更方法字节码的实现。通过前面一篇,知道ClassVisitor 的visitMethod()方法可以返回一个MethodVisitor的实例。那么我们也基本可以知道,同ClassVisitor改变类成员一样,MethodVIsistor如果需要改变方法成员,注入逻辑,也可以
- java编程思想 --内部类
百合不是茶
java内部类匿名内部类
内部类;了解外部类 并能与之通信 内部类写出来的代码更加整洁与优雅
1,内部类的创建 内部类是创建在类中的
package com.wj.InsideClass;
/*
* 内部类的创建
*/
public class CreateInsideClass {
public CreateInsideClass(
- web.xml报错
crabdave
web.xml
web.xml报错
The content of element type "web-app" must match "(icon?,display-
name?,description?,distributable?,context-param*,filter*,filter-mapping*,listener*,servlet*,s
- 泛型类的自定义
麦田的设计者
javaandroid泛型
为什么要定义泛型类,当类中要操作的引用数据类型不确定的时候。
采用泛型类,完成扩展。
例如有一个学生类
Student{
Student(){
System.out.println("I'm a student.....");
}
}
有一个老师类
- CSS清除浮动的4中方法
IT独行者
JavaScriptUIcss
清除浮动这个问题,做前端的应该再熟悉不过了,咱是个新人,所以还是记个笔记,做个积累,努力学习向大神靠近。CSS清除浮动的方法网上一搜,大概有N多种,用过几种,说下个人感受。
1、结尾处加空div标签 clear:both 1 2 3 4
.div
1
{
background
:
#000080
;
border
:
1px
s
- Cygwin使用windows的jdk 配置方法
_wy_
jdkwindowscygwin
1.[vim /etc/profile]
JAVA_HOME="/cgydrive/d/Java/jdk1.6.0_43" (windows下jdk路径为D:\Java\jdk1.6.0_43)
PATH="$JAVA_HOME/bin:${PATH}"
CLAS
- linux下安装maven
无量
mavenlinux安装
Linux下安装maven(转) 1.首先到Maven官网
下载安装文件,目前最新版本为3.0.3,下载文件为
apache-maven-3.0.3-bin.tar.gz,下载可以使用wget命令;
2.进入下载文件夹,找到下载的文件,运行如下命令解压
tar -xvf apache-maven-2.2.1-bin.tar.gz
解压后的文件夹
- tomcat的https 配置,syslog-ng配置
aichenglong
tomcathttp跳转到httpssyslong-ng配置syslog配置
1) tomcat配置https,以及http自动跳转到https的配置
1)TOMCAT_HOME目录下生成密钥(keytool是jdk中的命令)
keytool -genkey -alias tomcat -keyalg RSA -keypass changeit -storepass changeit
- 关于领号活动总结
alafqq
活动
关于某彩票活动的总结
具体需求,每个用户进活动页面,领取一个号码,1000中的一个;
活动要求
1,随机性,一定要有随机性;
2,最少中奖概率,如果注数为3200注,则最多中4注
3,效率问题,(不能每个人来都产生一个随机数,这样效率不高);
4,支持断电(仍然从下一个开始),重启服务;(存数据库有点大材小用,因此不能存放在数据库)
解决方案
1,事先产生随机数1000个,并打
- java数据结构 冒泡排序的遍历与排序
百合不是茶
java
java的冒泡排序是一种简单的排序规则
冒泡排序的原理:
比较两个相邻的数,首先将最大的排在第一个,第二次比较第二个 ,此后一样;
针对所有的元素重复以上的步骤,除了最后一个
例题;将int array[]
- JS检查输入框输入的是否是数字的一种校验方法
bijian1013
js
如下是JS检查输入框输入的是否是数字的一种校验方法:
<form method=post target="_blank">
数字:<input type="text" name=num onkeypress="checkNum(this.form)"><br>
</form>
- Test注解的两个属性:expected和timeout
bijian1013
javaJUnitexpectedtimeout
JUnit4:Test文档中的解释:
The Test annotation supports two optional parameters.
The first, expected, declares that a test method should throw an exception.
If it doesn't throw an exception or if it
- [Gson二]继承关系的POJO的反序列化
bit1129
POJO
父类
package inheritance.test2;
import java.util.Map;
public class Model {
private String field1;
private String field2;
private Map<String, String> infoMap
- 【Spark八十四】Spark零碎知识点记录
bit1129
spark
1. ShuffleMapTask的shuffle数据在什么地方记录到MapOutputTracker中的
ShuffleMapTask的runTask方法负责写数据到shuffle map文件中。当任务执行完成成功,DAGScheduler会收到通知,在DAGScheduler的handleTaskCompletion方法中完成记录到MapOutputTracker中
- WAS各种脚本作用大全
ronin47
WAS 脚本
http://www.ibm.com/developerworks/cn/websphere/library/samples/SampleScripts.html
无意中,在WAS官网上发现的各种脚本作用,感觉很有作用,先与各位分享一下
获取下载
这些示例 jacl 和 Jython 脚本可用于在 WebSphere Application Server 的不同版本中自
- java-12.求 1+2+3+..n不能使用乘除法、 for 、 while 、 if 、 else 、 switch 、 case 等关键字以及条件判断语句
bylijinnan
switch
借鉴网上的思路,用java实现:
public class NoIfWhile {
/**
* @param args
*
* find x=1+2+3+....n
*/
public static void main(String[] args) {
int n=10;
int re=find(n);
System.o
- Netty源码学习-ObjectEncoder和ObjectDecoder
bylijinnan
javanetty
Netty中传递对象的思路很直观:
Netty中数据的传递是基于ChannelBuffer(也就是byte[]);
那把对象序列化为字节流,就可以在Netty中传递对象了
相应的从ChannelBuffer恢复对象,就是反序列化的过程
Netty已经封装好ObjectEncoder和ObjectDecoder
先看ObjectEncoder
ObjectEncoder是往外发送
- spring 定时任务中cronExpression表达式含义
chicony
cronExpression
一个cron表达式有6个必选的元素和一个可选的元素,各个元素之间是以空格分隔的,从左至右,这些元素的含义如下表所示:
代表含义 是否必须 允许的取值范围 &nb
- Nutz配置Jndi
ctrain
JNDI
1、使用JNDI获取指定资源:
var ioc = {
dao : {
type :"org.nutz.dao.impl.NutDao",
args : [ {jndi :"jdbc/dataSource"} ]
}
}
以上方法,仅需要在容器中配置好数据源,注入到NutDao即可.
- 解决 /bin/sh^M: bad interpreter: No such file or directory
daizj
shell
在Linux中执行.sh脚本,异常/bin/sh^M: bad interpreter: No such file or directory。
分析:这是不同系统编码格式引起的:在windows系统中编辑的.sh文件可能有不可见字符,所以在Linux系统下执行会报以上异常信息。
解决:
1)在windows下转换:
利用一些编辑器如UltraEdit或EditPlus等工具
- [转]for 循环为何可恨?
dcj3sjt126com
程序员读书
Java的闭包(Closure)特征最近成为了一个热门话题。 一些精英正在起草一份议案,要在Java将来的版本中加入闭包特征。 然而,提议中的闭包语法以及语言上的这种扩充受到了众多Java程序员的猛烈抨击。
不久前,出版过数十本编程书籍的大作家Elliotte Rusty Harold发表了对Java中闭包的价值的质疑。 尤其是他问道“for 循环为何可恨?”[http://ju
- Android实用小技巧
dcj3sjt126com
android
1、去掉所有Activity界面的标题栏
修改AndroidManifest.xml 在application 标签中添加android:theme="@android:style/Theme.NoTitleBar"
2、去掉所有Activity界面的TitleBar 和StatusBar
修改AndroidManifes
- Oracle 复习笔记之序列
eksliang
Oracle 序列sequenceOracle sequence
转载请出自出处:http://eksliang.iteye.com/blog/2098859
1.序列的作用
序列是用于生成唯一、连续序号的对象
一般用序列来充当数据库表的主键值
2.创建序列语法如下:
create sequence s_emp
start with 1 --开始值
increment by 1 --増长值
maxval
- 有“品”的程序员
gongmeitao
工作
完美程序员的10种品质
完美程序员的每种品质都有一个范围,这个范围取决于具体的问题和背景。没有能解决所有问题的
完美程序员(至少在我们这个星球上),并且对于特定问题,完美程序员应该具有以下品质:
1. 才智非凡- 能够理解问题、能够用清晰可读的代码翻译并表达想法、善于分析并且逻辑思维能力强
(范围:用简单方式解决复杂问题)
- 使用KeleyiSQLHelper类进行分页查询
hvt
sql.netC#asp.nethovertree
本文适用于sql server单主键表或者视图进行分页查询,支持多字段排序。KeleyiSQLHelper类的最新代码请到http://hovertree.codeplex.com/SourceControl/latest下载整个解决方案源代码查看。或者直接在线查看类的代码:http://hovertree.codeplex.com/SourceControl/latest#HoverTree.D
- SVG 教程 (三)圆形,椭圆,直线
天梯梦
svg
SVG <circle> SVG 圆形 - <circle>
<circle> 标签可用来创建一个圆:
下面是SVG代码:
<svg xmlns="http://www.w3.org/2000/svg" version="1.1">
<circle cx="100" c
- 链表栈
luyulong
java数据结构
public class Node {
private Object object;
private Node next;
public Node() {
this.next = null;
this.object = null;
}
public Object getObject() {
return object;
}
public
- 基础数据结构和算法十:2-3 search tree
sunwinner
Algorithm2-3 search tree
Binary search tree works well for a wide variety of applications, but they have poor worst-case performance. Now we introduce a type of binary search tree where costs are guaranteed to be loga
- spring配置定时任务
stunizhengjia
springtimer
最近因工作的需要,用到了spring的定时任务的功能,觉得spring还是很智能化的,只需要配置一下配置文件就可以了,在此记录一下,以便以后用到:
//------------------------定时任务调用的方法------------------------------
/**
* 存储过程定时器
*/
publi
- ITeye 8月技术图书有奖试读获奖名单公布
ITeye管理员
活动
ITeye携手博文视点举办的8月技术图书有奖试读活动已圆满结束,非常感谢广大用户对本次活动的关注与参与。
8月试读活动回顾:
http://webmaster.iteye.com/blog/2102830
本次技术图书试读活动的优秀奖获奖名单及相应作品如下(优秀文章有很多,但名额有限,没获奖并不代表不优秀):
《跨终端Web》
gleams:http