左旋转字符串
转自:程序员编程艺术第一章、左旋转字符串
主要为本人收藏学习用
大家开始可能会有这样的潜在假设,K<N。事实上,很多时候也的确是这样的。但严格来说,我们不能用这样的“惯性思维”来思考问题。
尤其在编程的时候,全面地考虑问题是很重要的,K可能是一个远大于N的整数,在这个时候,上面的解法是需要改进的。
仔细观察循环右移的特点,不难发现:每个元素右移N位后都会回到自己的位置上。因此,如果K > N,右移K-N之后的数组序列跟右移K位的结果是一样的。
进而可得出一条通用的规律:
右移K位之后的情形,跟右移K’= K % N位之后的情形一样
还有就是 K' > N/2,的话
左移K' 等于 右移 N-K';
2.1、在此,本人再奉献另外一种思路,即为本思路二:
abc defghi,要abc移动至最后
abc defghi->def abcghi->def ghiabc
定义俩指针,p1指向ch[0],p2指向ch[m];
一下过程循环m次,交换p1和p2所指元素,然后p1++, p2++;。
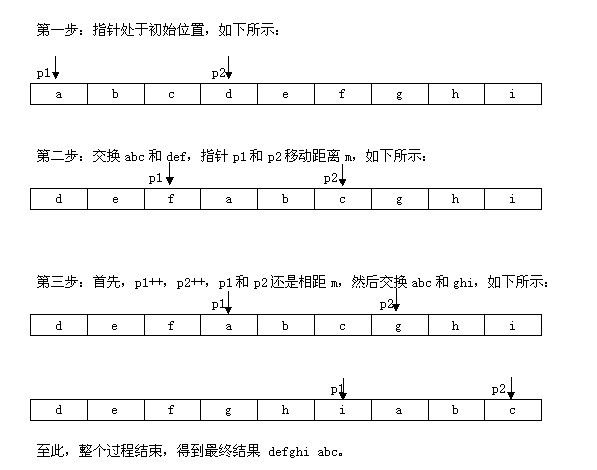
第一步,交换abc 和def ,
abc defghi->def abcghi
第二步,交换abc 和 ghi,
def abcghi->def ghiabc
整个过程,看起来,就是abc 一步一步 向后移动
abc defghi
def abcghi
def ghi abc
//最后的 复杂度是O(m+n)
以下是朋友颜沙针对上述过程给出的图解:
2.2、各位读者注意了:
由上述例子九个元素的序列abcdefghi,您已经看到,m=3时,p2恰好指到了数组最后一个元素,于是,上述思路没有问题。但如果上面例子中i 的后面还有元素列?
即,如果是要左旋十个元素的序列:abcdefghij,ok,下面,就举这个例子,对abcdefghij序列进行左旋转操作:
如果abcdef ghij要变成defghij abc:
abcdef ghij
1. def abc ghij
2. def ghi abc j //接下来,j 步步前移
3. def ghi ab jc
4. def ghi a j bc
5. def ghi j abc
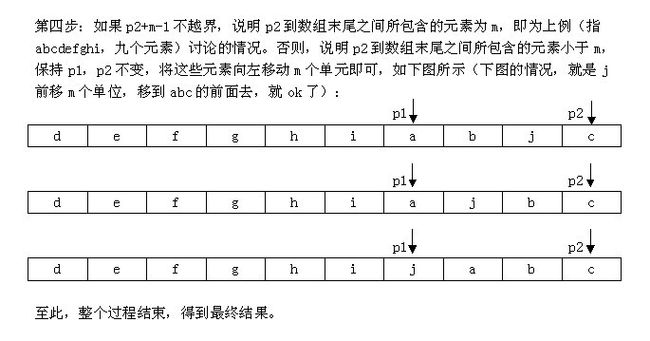
下面,再针对上述过程,画个图清晰说明下,如下所示:
ok,咱们来好好彻底总结一下此思路二:(就4点,请仔细阅读):
1、首先让p1=ch[0],p2=ch[m],即让p1,p2相隔m的距离;
2、判断p2+m-1是否越界,如果没有越界转到3,否则转到4(abcdefgh这8个字母的字符串,以4左旋,那么初始时p2指向e,p2+4越界了,但事实上p2至p2+m-1是m个字符,可以再做一个交换)。
3、不断交换*p1与*p2,然后p1++,p2++,循环m次,然后转到2。
4、此时p2+m-1 已经越界,在此只需处理尾巴。过程如下:
4.1 通过n-p2得到p2与尾部之间元素个数r,即我们要前移的元素个数。
4.2 以下过程执行r次:
ch[p2]<->ch[p2-1],ch[p2-1]<->ch[p2-2],....,ch[p1+1]<->ch[p1];p1++;p2++;
(特别感谢tctop组成员big的指正,tctop组的修订wiki页面为:http://tctop.wikispaces.com/)
所以,之前最初的那个左旋转九个元素abcdefghi的思路在末尾会出现问题的(如果p2后面有元素就不能这么变,例如,如果是处理十个元素,abcdefghij 列?对的,就是这个意思),解决办法有两个:
方法一(即如上述思路总结所述):
def ghi abc jk
当p1指向a,p2指向j时,由于p2+m越界,那么此时p1,p2不要变
这里p1之后(abcjk)就是尾巴,处理尾巴只需将j,k移到abc之前,得到最终序列,代码编写如下:
- //copyright@July、颜沙
- //最终代码,July,updated again,2011.04.17。
- #include <iostream>
- #include <string>
- using namespace std;
- void rotate(string &str, int m)
- {
- if (str.length() == 0 || m <= 0)
- return;
- int n = str.length();
- if (m % n <= 0)
- return;
- int p1 = 0, p2 = m;
- int k = (n - m) - n % m;
- // 交换p1,p2指向的元素,然后移动p1,p2
- while (k --)
- {
- swap(str[p1], str[p2]);
- p1++;
- p2++;
- }
- // 重点,都在下述几行。
- // 处理尾部,r为尾部左移次数
- int r = n - p2;
- while (r--)
- {
- int i = p2;
- while (i > p1)
- {
- swap(str[i], str[i-1]);
- i--;
- }
- p2++;
- p1++;
- }
- //比如一个例子,abcdefghijk
- // p1 p2
- //当执行到这里时,defghi a b c j k
- //p2+m出界 了,
- //r=n-p2=2,所以以下过程,要执行循环俩次。
- //第一次:j 步步前移,abcjk->abjck->ajbck->jabck
- //然后,p1++,p2++,p1指a,p2指k。
- // p1 p2
- //第二次:defghi j a b c k
- //同理,此后,k步步前移,abck->abkc->akbc->kabc。
- }
- int main()
- {
- string ch="abcdefghijk";
- rotate(ch,3);
- cout<<ch<<endl;
- return 0;
- }
def ghi abc jk
当p1指向a,p2指向j时,那么交换p1和p2,
此时为:
def ghi jbc ak
p1++,p2++,p1指向b,p2指向k,继续上面步骤得:
def ghi jkc ab
p1++,p2不动,p1指向c,p2指向b,p1和p2之间(cab)也就是尾巴,
那么处理尾巴(cab)需要循环左移一定次数(而后的具体操作步骤已在下述程序的注释中已详细给出)。
根据方案二,不难写出下述代码(已测试正确):
- #include <iostream>
- #include <string>
- using namespace std;
- //颜沙,思路二之方案二,
- //July、updated,2011.04.16。
- void rotate(string &str, int m)
- {
- if (str.length() == 0 || m < 0)
- return;
- //初始化p1,p2
- int p1 = 0, p2 = m;
- int n = str.length();
- // 处理m大于n
- if (m % n == 0)
- return;
- // 循环直至p2到达字符串末尾
- while(true)
- {
- swap(str[p1], str[p2]);
- p1++;
- if (p2 < n - 1)
- p2++;
- else
- break;
- }
- // 处理尾部,r为尾部循环左移次数
- int r = m - n % m; // r = 1.
- while (r--) //外循环执行一次
- {
- int i = p1;
- char temp = str[p1];
- while (i < p2) //内循环执行俩次
- {
- str[i] = str[i+1];
- i++;
- }
- str[p2] = temp;
- }
- //举一个例子
- //abcdefghijk
- //当执行到这里的时候,defghiabcjk
- // p1 p2
- //defghi a b c j k,a 与 j交换,jbcak,然后,p1++,p2++
- // p1 p2
- // j b c a k,b 与 k交换,jkcab,然后,p1++,p2不动,
- //r = m - n % m= 3-11%3=1,即循环移位1次。
- // p1 p2
- // j k c a b
- //p1所指元素c实现保存在temp里,
- //然后执行此条语句:str[i] = str[i+1]; 即a跑到c的位置处,a_b
- //i++,再次执行:str[i] = str[i+1],ab_
- //最后,保存好的c 填入,为abc,所以,最终序列为defghi jk abc。
- //July、updated,2011.04.17晚,送走了她。
- }
- int main()
- {
- string ch="abcdefghijk";
- rotate(ch,3);
- cout<<ch<<endl;
- return 0;
- }
注意:上文中都是假设m<n,且如果鲁棒点的话令m=m%n,这样m允许大于n。另外,各位要记得处理指针为空的情况。
还可以看下这段代码:
- /*
- * myinvert2.cpp
- *
- * Created on: 2011-5-11
- * Author: BigPotato
- */
- #include<iostream>
- #include<string>
- #define positiveMod(m,n) ((m) % (n) + (n)) % (n)
- /*
- *左旋字符串str,m为负数时表示右旋abs(m)个字母
- */
- void rotate(std::string &str, int m) {
- if (str.length() == 0)
- return;
- int n = str.length();
- //处理大于str长度及m为负数的情况,positiveMod可以取得m为负数时对n取余得到正数
- m = positiveMod(m,n);
- if (m == 0)
- return;
- // if (m % n <= 0)
- // return;
- int p1 = 0, p2 = m;
- int round;
- //p2当前所指和之后的m-1个字母共m个字母,就可以和p2前面的m个字母交换。
- while (p2 + m - 1 < n) {
- round = m;
- while (round--) {
- std::swap(str[p1], str[p2]);
- p1++;
- p2++;
- }
- }
- //剩下的不足m个字母逐个交换
- int r = n - p2;
- while (r--) {
- int i = p2;
- while (i > p1) {
- std::swap(str[i], str[i - 1]);
- i--;
- }
- p2++;
- p1++;
- }
- }
- //测试
- int main(int argc, char **argv) {
- // std::cout << ((-15) % 7 + 7) % 7 << std::endl;
- // std::cout << (-15) % 7 << std::endl;
- std::string ch = "abcdefg";
- int len = ch.length();
- for (int m = -2 * len; m <= len * 2; m++) {
- //由于传给rotate的是string的引用,所以这里每次调用都用了一个新的字符串
- std::string s = "abcdefg";
- rotate(s, m);
- std::cout << positiveMod(m,len) << ": " << s << std::endl;
- }
- return 0;
- }