坐标变换的实现

Windows 窗体编程

坐标系类型

 

GDI+ 使用三个坐标空间：世界、页面和设备。世界坐标是用于建立特殊图形世界模型的坐标系，也是在 .NET Framework 中传递给方法的坐标系。页面坐标系是指绘图图面（如窗体或控件）使用的坐标系。设备坐标系是在其上进行绘制的物理设备（如屏幕或纸张）所使用的坐标系。当调用 myGraphics.DrawLine(myPen, 0, 0, 160, 80) 时，传递给 DrawLine 方法的点（(0, 0) 和 (160, 80)）位于世界坐标空间内。在 GDI+ 可以在屏幕上绘制线条之前，坐标先要经过一系列变换。一种称为“世界变换”的变换可将世界坐标转换为页面坐标，而另一种称为“页面变换”的变换可将页面坐标转换为设备坐标。

变换和坐标系

假定您想使用原点位于工作区的主体而非左上角的坐标系统。例如，您需要让原点位于距工作区左边缘 100 像素、距顶部 50 像素的位置。下图显示了这样的坐标系统。

当调用 myGraphics.DrawLine(myPen, 0, 0, 160, 80) 时，可得到下面的插图中所显示的线条。

下表显示了三种坐标空间中线条终点的坐标：

世界	(0, 0) 到 (160, 80)
页面	(100, 50) 到 (260, 130)
设备	(100, 50) 到 (260, 130)

请注意，页面坐标空间的原点在工作区的左上角，情况将总是如此。另外请注意，由于度量单位是像素，所以设备坐标与页面坐标是相同的。如果将度量单位设置为像素以外的其他单位（例如英寸），设备坐标将不同于页面坐标。

用于将世界坐标映射到页面坐标的世界变换保存在 Graphics 类的 Transform 属性中。在前面的示例中，世界变换是在 x 方向平移 100 个单位、在 y 方向平移 50 个单位。下面的示例设置了 Graphics 对象的世界变换，然后使用该 Graphics 对象绘制前图中显示的线条：

Visual Basic

复制代码

myGraphics.TranslateTransform(100, 50)
myGraphics.DrawLine(myPen, 0, 0, 160, 80)

C#

复制代码

myGraphics.TranslateTransform(100, 50);
myGraphics.DrawLine(myPen, 0, 0, 160, 80);

页面变换将页面坐标映射到设备坐标。Graphics 类提供了用于操作页面变换的 PageUnit 和 PageScale 属性。Graphics 类还提供了两个只读属性：DpiX 和 DpiY，用于检查显示设备每英寸的水平点数和垂直点数。

可使用 Graphics 类的 PageUnit 属性指定除像素以外的其他度量单位。

注意
不能将 PageUnit 属性设置为 World，因为这不是物理单元，将导致异常。

下面的示例从 (0, 0) 至 (2, 1) 绘制线条，其中点 (2, 1) 位于点 (0, 0) 的右边 2 英寸和下边 1 英寸处：

Visual Basic

复制代码

myGraphics.PageUnit = GraphicsUnit.Inch
myGraphics.DrawLine(myPen, 0, 0, 2, 1)

C#

复制代码

myGraphics.PageUnit = GraphicsUnit.Inch;
myGraphics.DrawLine(myPen, 0, 0, 2, 1);

注意
如果在构造钢笔时没有指定钢笔的宽度，前面的示例将绘制一条一英寸宽的线条。可以在 Pen 构造函数的第二个参数中指定钢笔的宽度：

Visual Basic

复制代码

Dim myPen As New Pen(Color.Black, 1 / myGraphics.DpiX)

C#

复制代码

Pen myPen = new Pen(Color.Black, 1 / myGraphics.DpiX);

如果我们假定显示设备在水平方向和垂直方向每英寸都有 96 个点，则上例中直线的终结点在三个坐标空间中分别具有以下坐标：

世界	(0, 0) 到 (2, 1)
页面	(0, 0) 到 (2, 1)
设备	(0, 0) 到 (192, 96)

请注意，由于世界坐标空间的原点在工作区的左上角，因此页面坐标与世界坐标相同。

您可以合并世界变换和页面变换，以实现多种效果。例如，假定您想使用英寸作为度量单位，并且想让坐标系统的原点距工作区左边缘 2 英寸、距工作区顶部 1/2 英寸。下面的示例设置 Graphics 对象的世界变换和页面变换，然后绘制一条从 (0, 0) 到 (2, 1) 的直线：

Visual Basic

复制代码

myGraphics.TranslateTransform(2, 0.5F)
myGraphics.PageUnit = GraphicsUnit.Inch
myGraphics.DrawLine(myPen, 0, 0, 2, 1)

C#

复制代码

myGraphics.TranslateTransform(2, 0.5f);
myGraphics.PageUnit = GraphicsUnit.Inch;
myGraphics.DrawLine(myPen, 0, 0, 2, 1);

下图显示了线条和坐标系统。

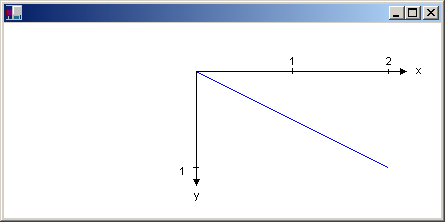
如果我们假定显示设备在水平方向和垂直方向每英寸都有 96 个点，则上例中直线的终结点在三个坐标空间中分别具有以下坐标：

世界	(0, 0) 到 (2, 1)
页面	(2, 0.5) 到 (4, 1.5)
设备	(192, 48) 到 (384, 144)

 

变换的矩阵表示形式

 

m×n 矩阵是排列在 m 行和 n 列中的一系列数。下图显示几个矩阵。

您可以通过将单个元素相加来加合两个尺寸相同的矩阵。下图显示了两个矩阵相加的示例。

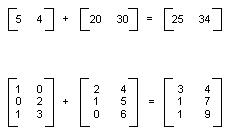
m×n 矩阵可与一个 n×p 矩阵相乘，结果为一个 m×p 矩阵。第一个矩阵的列数必须与第二个矩阵的行数相同。例如，一个 4×2 矩阵与一个 2×3 矩阵相乘，产生一个 4×3 矩阵。

矩阵的行列的平面点可视为矢量。例如，(2, 5) 是具有两个组件的矢量，(3, 7, 1) 是具有三个组件的矢量。两个矢量的点积定义如下：

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

例如，(2, 3) 和 (5, 4) 的点积是 (2)(5) + (3)(4) = 22。(2, 5, 1) 和 (4, 3, 1) 的点积是 (2)(4) + (5)(3) + (1)(1) = 24。请注意，两个矢量的点积是数字，而不是另一个矢量。另外请注意，只有当两个矢量的组件数相同时，才能计算点积。

将 A(i, j) 作为矩阵 A 中第 i 行、第 j 列的项。例如，A（3, 2）是矩阵 A 中第 3 行、第 2 列的项。假定 A、B 和 C 是矩阵，且 AB = C，则 C 的项计算如下：

C(i, j) =（A 的第 i 行）•（B 的第 j 列）

下图显示了矩阵相乘的几个示例。

如果将平面中的点视为 1×2 矩阵，则可通过将该点乘以一个 2×2 矩阵来将该点变换。下图显示了应用于点 (2, 1) 的几个变换。

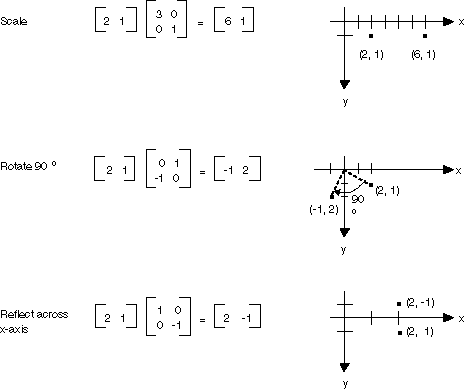
前图中显示的所有变换都是线性变换。某些其他变换（如平移）不是线性的，不能表示为与 2×2 矩阵相乘的形式。假定您要从点 (2, 1) 开始，将其旋转 90 度，在 x 方向将其平移 3 个单位，在 y 方向将其平移 4 个单位。可通过先使用矩阵乘法再使用矩阵加法来完成此操作。

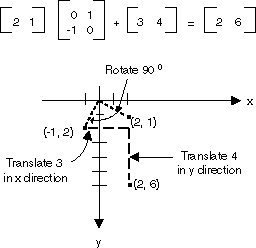
后面跟一平移（与 1×2 矩阵相加）的线性变换（与 2×2 矩阵相乘）称为仿射变换。将仿射变换存储于一对矩阵（一个用于线性部分，一个用于平移）的替换方案是将整个变换存储于 3×3 矩阵。若要使其起作用，平面上的点必须存储于具有虚拟第三坐标的 1×3 矩阵中。通常的方法是使所有的第三坐标等于 1。例如，矩阵 [2 1 1] 代表点 (2, 1)。下图演示了表示为与单个 3×3 矩阵相乘的仿射变换（旋转 90 度；在 x 方向上平移 3 个单位，在 y 方向上平移 4 个单位）。

在前面的示例中，点 (2, 1) 映射到了点 (2, 6)。请注意，3×3 矩阵的第三列包含数字 0，0，1。对于仿射变换的 3×3 矩阵而言，情况将总是如此。重要的数字是列 1 和列 2 中的 6 个数字。矩阵左上角的 2×2 部分表示变换的线性部分，第 3 行中的前两项表示平移。

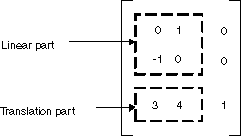
在 GDI+ 中，可以在 Matrix 对象中存储仿射变换。由于表示仿射变换的矩阵的第三列总是（0，0，1），因此在构造 Matrix 对象时，只需指定前两列中的 6 个数。Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) 语句构造上面图形中显示的矩阵。

复合变换

复合变换是一个接一个的变换序列。请考虑下面列表中的矩阵和变换：

矩阵 A	旋转 90 度
矩阵 B	在 x 方向上缩放 2 倍
矩阵 C	在 y 方向上平移 3 个单位

如果从由矩阵 [2 1 1] 表示的点 (2, 1) 开始，并先后乘以 A、B、C，则点 (2, 1) 将按列出的顺序经历三种变换。

[2 1 1]ABC = [-2 5 1]

可以不将复合变换的三部分存储于三个独立的矩阵，而是一起乘以 A、B 和 C 来得到存储整个复合变换的单个的 3×3 矩阵。假定 ABC = D。则一个点乘以 D 得出的结果与一个点先后乘以 A、B、C 的结果相同。

[2 1 1]D = [-2 5 1]

下图显示了矩阵 A、B、C 和 D。

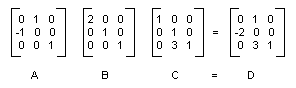
复合变换的矩阵可通过将几个单独的变换矩阵相乘而得到，这就意味着任何仿射变换的序列均可存储于单个的 Matrix 对象中。

警告
复合变换的顺序非常重要。一般说来，先旋转、再缩放、然后平移，与先缩放、再旋转、然后平移是不同的。同样，矩阵相乘的顺序也是重要的。一般说来，ABC 与 BAC 不同。

Matrix 类提供了几种构建复合变换的方法：Multiply、Rotate、RotateAt、Scale、Shear 和 Translate。下面的示例创建了复合变换（先旋转 30 度，再在 y 方向上缩放 2 倍，然后在 x 方向平移 5 个单位）的矩阵。

Visual Basic

复制代码

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)

C#

复制代码

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

下图显示该矩阵。

全局变换和局部变换

 

全局变换是应用于由给定的 Graphics 对象绘制的每个项目的变换。与此相反，局部变换则是应用于要绘制的特定项目的变换。

全局变换

若要创建全局变换，请构造 Graphics 对象，再操作其 Transform 属性。Transform 属性是 Matrix 对象，因此，它能够保存仿射变换的任何序列。存储在 Transform 属性中的变换被称为世界变换。Graphics 类提供了几个构建复合世界变换的方法：MultiplyTransform、RotateTransform、ScaleTransform 和 TranslateTransform。下面的示例绘制了两次椭圆：一次在创建世界变换之前，一次在创建世界变换之后。变换首先在 y 方向上缩放 0.5 倍，再在 x 方向平移 50 个单位，然后旋转 30 度。

Visual Basic

复制代码

myGraphics.DrawEllipse(myPen, 0, 0, 100, 50)
myGraphics.ScaleTransform(1, 0.5F)
myGraphics.TranslateTransform(50, 0, MatrixOrder.Append)
myGraphics.RotateTransform(30, MatrixOrder.Append)
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50)

C#

复制代码

myGraphics.DrawEllipse(myPen, 0, 0, 100, 50);
myGraphics.ScaleTransform(1, 0.5f);
myGraphics.TranslateTransform(50, 0, MatrixOrder.Append);
myGraphics.RotateTransform(30, MatrixOrder.Append);
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50);

下图显示了变换中涉及的矩阵。

注意
在前面的示例中，椭圆围绕坐标系的原点旋转。原点位于工作区的左上角。与椭圆围绕其自身中心旋转相比，这样会产生不同的结果。

局部变换

局部变换应用于要绘制的特定项目。例如，GraphicsPath 对象具有 Transform 方法，可用来对该路径的数据点进行变换。下面的示例绘制了一个没有变换的矩形以及一个有旋转变换的路径。（假定没有世界变换）。

Visual Basic

复制代码

Dim myMatrix As New Matrix()
myMatrix.Rotate(45)
myGraphicsPath.Transform(myMatrix)
myGraphics.DrawRectangle(myPen, 10, 10, 100, 50)
myGraphics.DrawPath(myPen, myGraphicsPath)

C#

复制代码

Matrix myMatrix = new Matrix();
myMatrix.Rotate(45);
myGraphicsPath.Transform(myMatrix);
myGraphics.DrawRectangle(myPen, 10, 10, 100, 50);
myGraphics.DrawPath(myPen, myGraphicsPath);

世界变换可与局部变换合并，以得到多种结果。例如，世界变换可用于修正坐标系统，而局部变换可用于旋转和缩放在新坐标系统上绘制的对象。

假定您需要原点距工作区左边缘 200 像素、距工作区顶部 150 像素的坐标系统。此外，假定您需要的度量单位是像素，且 x 轴指向右方，y 轴指向上方。默认的坐标系统是 y 轴指向下方，因此您需要执行绕水平坐标轴的反射。下图显示了这样的矩阵反射。

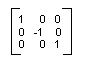
下一步，假定您需要执行一个向右 200 个单位、向下 150 个单位的平移。

下面的示例通过设置 Graphics 对象的世界变换，建立前面刚刚描述过的坐标系统。

Visual Basic

复制代码

Dim myMatrix As New Matrix(1, 0, 0, -1, 0, 0)
myGraphics.Transform = myMatrix
myGraphics.TranslateTransform(200, 150, MatrixOrder.Append)

C#

复制代码

Matrix myMatrix = new Matrix(1, 0, 0, -1, 0, 0);
myGraphics.Transform = myMatrix;
myGraphics.TranslateTransform(200, 150, MatrixOrder.Append);

下面的代码（置于前面示例的结尾处）创建了由一个单独矩形组成的路径，该矩形的左下角在新坐标系统的原点。矩形经过两次填充：一次不使用局部变换，一次使用局部变换。局部变换包括在水平方向上缩放 2 倍，然后再旋转 30 度。

Visual Basic

复制代码

' Create the path.
Dim myGraphicsPath As New GraphicsPath()
Dim myRectangle As New Rectangle(0, 0, 60, 60)
myGraphicsPath.AddRectangle(myRectangle)

' Fill the path on the new coordinate system.
' No local transformation
myGraphics.FillPath(mySolidBrush1, myGraphicsPath)

' Set the local transformation of the GraphicsPath object.
Dim myPathMatrix As New Matrix()
myPathMatrix.Scale(2, 1)
myPathMatrix.Rotate(30, MatrixOrder.Append)
myGraphicsPath.Transform(myPathMatrix)

' Fill the transformed path on the new coordinate system.
myGraphics.FillPath(mySolidBrush2, myGraphicsPath)

C#

复制代码

// Create the path.
GraphicsPath myGraphicsPath = new GraphicsPath();
Rectangle myRectangle = new Rectangle(0, 0, 60, 60);
myGraphicsPath.AddRectangle(myRectangle);

// Fill the path on the new coordinate system.
// No local transformation
myGraphics.FillPath(mySolidBrush1, myGraphicsPath);

// Set the local transformation of the GraphicsPath object.
Matrix myPathMatrix = new Matrix();
myPathMatrix.Scale(2, 1);
myPathMatrix.Rotate(30, MatrixOrder.Append);
myGraphicsPath.Transform(myPathMatrix);

// Fill the transformed path on the new coordinate system.
myGraphics.FillPath(mySolidBrush2, myGraphicsPath);

下图显示了新的坐标系统和两个矩形。