【算法导论】排序算法 二

排序算法二

基本的声明及公用函数库在【算法导论】排序算法 零中介绍。

一、选择法排序、冒泡排序、插入法排序

二、快速排序、分治法排序、堆排序

三、计数排序、基数排序、桶排序

gtest介绍及测试用例如下：测试框架之GTest

MIT《算法导论》下载：hereorhttp://download.csdn.net/detail/ceofit/4212385 

源码下载：here orhttp://download.csdn.net/detail/ceofit/4218488

选择法排序、冒泡排序、插入排序都比较简单，时间复杂度也比较大，都是O(n*n)。于是有了减小时间复杂度的排序算法，最常用的当属快速排序。
本节介绍几个时间复杂度为nlogn的排序算法：快速排序、堆排序、分治法排序。这几个算法其基础都是基于二分的思想，或说是基于有序二叉树，实现过程一般都是递归。使用递归一层一层的处理。

快速排序

快速排序使用很普遍，比较简单，而且是原地排序，所以性能要求严格的地方经常使用快排。

比如n个数据，快排将第1个数据m作为中间数据，将所有数据中按照大于m、小于m分开，即找到m的位置，所以一轮后，所有数据排列为<m,m,>m，然后对<m与>m递归这个过程即可。最优情况下时间复杂度nlogn，最坏情况下时间复杂度n*n。

具体查找m的位置的算法很多，下面介绍两种，很简单，不详细介绍，直接看代码。

例如
2 4 5 3 1

第一层快排后为：

1 2 5 3 4

第二层快排，2左边只有1个数据，已经牌号，右边5 3 4，排序后为：

1 2 3 4 5

ok，排序完成。

//快速排序，时间复杂度最大n*n，最优情况下为nlgn，原地排序
void QuickSort(int *pArray,int cnt);

#include "SK_Common.h"
#include "SK_Sort.h"

int get_middle(int *pArray,int start,int end)
{
	if(start >= end)
		return start;
	int midvalue = pArray[start];
	int save_ptr = start;
	int front_ptr = start;
	
	while(front_ptr <= end)
	{
		if(pArray[front_ptr] < midvalue)
		{
			pArray[save_ptr] = pArray[front_ptr];
			pArray[front_ptr] = pArray[save_ptr+1];
			save_ptr++;
		}
		front_ptr++;
	}
	pArray[save_ptr] = midvalue;
	return save_ptr;
}

void _quick_sort(int *pArray,int start,int end)
{
	if(start >= end)
		return;
	int mid = get_middle(pArray,start,end);
	_quick_sort(pArray,start,mid-1);
	_quick_sort(pArray,mid+1,end);
}

void QuickSort(int *pArray,int cnt)
{
	_quick_sort(pArray,0,cnt-1);
}

其中get_middle还有另外一种实现方法：

int get_middle(int *pArray,int start,int end)
{
	if(start >= end)
		return start;
	int midvalue = pArray[start];
	int first_ptr = start;
	int second_ptr = end;

	while(first_ptr <= second_ptr)
	{
		while(pArray[first_ptr] < midvalue)
			first_ptr++;
		while(pArray[second_ptr] > midvalue)
			second_ptr--;
		if(first_ptr < second_ptr)
        {
            exchange(pArray+first_ptr,pArray+second_ptr);
            first_ptr++;
            second_ptr--;
		}
        else
        {
            break;
        }
	}
		
	return second_ptr;
}

快排对乱序的数据排序效果很好，但对有序的数据排序效果很差，复杂度到n*n，所以每层排序获取的中间数据可以随机化选择，而不是用第1个元素，这样可以有效的提高有序序列的排序速度。

int get_middle_random(int *pArray,int start,int end)
{
	int mid = get_random(start,end);
	exchange(pArray+start,pArray+mid);
	return get_middle(pArray,start,end);
}

void _quick_sort(int *pArray,int start,int end)
{
	if(start >= end)
		return;
	int mid = get_middle_random(pArray,start,end);
	_quick_sort(pArray,start,mid-1);
	_quick_sort(pArray,mid+1,end);
}

 

分治法排序

分治法排序也是二分思想，假设n个数据的前n/2个数据和后n/2个数据都是有序的，那将两段数据合并后即可得到一个有序序列。合并的复杂度为n。基于二分思想，所以分治法排序的算法复杂度也是nlogn.

例如
2 4 5 3 1

如此分：2 4      5 3 1 ，5 3 1 分为5         3 1 

第一次合并后

2 4 ||5 | 1 3

第二次合并后为

2 4 |1 3 5

第三次合并后为

1 2 3 4 5

排序OK。

由于分治法排序需要存储临时数据，所以标准分治法排序不是原地排序，时间复杂度为nlogn,空间复杂度为n

书中给出的一个例子图解：

 

//分治排序，时间复杂度nlgn，非原地排序
void MergeSort(int *pArray,int cnt);

#include "SK_Common.h"
#include "SK_Sort.h"

void _merge(int *pArray,int start,int mid,int end)
{
    if(!(mid >= start && mid <= end))
        return;
    int len1 = mid-start+1;
    int len2 = end - mid;
    int *pArray1 = new int[len1+1];// +1防止最后一个for循环中，
                                                      // 因为判断顺序不同机器不同而导致的数组下标越界
    int *pArray2 = new int[len2+1];
    int i = 0,j = 0,k = 0;
    for(i=0;i<len1;i++)
    {
        pArray1[i] = pArray[start+i];
    }

    for(i=0;i<len2;i++)
    {
        pArray2[i] = pArray[mid+i+1];
    }

    i = j = 0;
    for(k=start; k<=end; k++)
    {
        if(j>=len2 || (i < len1 && pArray1[i] <= pArray2[j]))
            pArray[k] = pArray1[i++];
        else
            pArray[k] = pArray2[j++];
    }
    delete[] pArray1;
    delete[] pArray2;
}

void _mergesort(int *pArray,int start,int end)
{
    if(start >= end)
        return;
    int mid = (start+end)/2;
    _mergesort(pArray,start,mid);
    _mergesort(pArray,mid+1,end);
    _merge(pArray,start,mid,end);
}

void MergeSort(int *pArray,int cnt)
{
    _mergesort(pArray,0,cnt-1);
}

为防止多次new、delete性能降低，可预分配临时空间：

void _merge(int *pArray,int start,int mid,int end,int *tmpArray)
{
    if(!(mid >= start && mid <= end))
        return;
    int len1 = mid-start+1;
    int len2 = end - mid;
    int *pArray1 = tmpArray;
    int *pArray2 = tmpArray+len1;
    int i = 0,j = 0,k = 0;
    for(i=start;i<=end;i++)
    {
        tmpArray[j++] = pArray[i];
    }

    i = j = 0;
    for(k=start; k<=end; k++)
    {
        if(j>=len2 || (i < len1 && pArray1[i] <= pArray2[j]))
            pArray[k] = pArray1[i++];
        else
            pArray[k] = pArray2[j++];
    }
}

void _mergesort(int *pArray,int start,int end,int *tmpArray)
{
    if(start >= end)
        return;
    int mid = (start+end)/2;
    _mergesort(pArray,start,mid,tmpArray);
    _mergesort(pArray,mid+1,end,tmpArray);
    _merge(pArray,start,mid,end,tmpArray);
}

void MergeSort(int *pArray,int cnt)
{
    int *tmpArray = new int[cnt+1];
    _mergesort(pArray,0,cnt-1,tmpArray);
    delete[] tmpArray;
}

堆排序

对排序是利用完全二叉树来实现的，复杂度nlogn且是原地排序。

将待排序数据表示为二叉树，例如 1 2 3 4 5 6 7，其中1为根节点，2 3为第一层子节点 4 5 6 7为叶子节点。其中4、5的父节点为2，6、7的父节点为3。

所以对于一个有序序列，假设n个元素，跟节点是1，深度为[log2(n)]，节点m的子节点为2m与2m+1，父节点为[m/2]。
其中对于任一节点m，存在m>2m,且m>2*m+1，这称为最大堆，可利用最大堆排升序。由于最大堆的性质可知最大堆的根节点永远是此二叉树的最大值。

找到最大值后，将此值置入最后一个叶子节点，然后将此节点从二叉树删除，依次递归，将第二大的值插入倒数第二个位置....依次类推可得到升序排序的序列。

因此堆排序需要两个过程：建立最大堆、堆排序。

建立最大堆是从n/2开始到0遍历，将值与两个子节点比较，如果比两个孩子至少1个小，则下移，直到满足此节点>=任意子节点。并递归遍历此过程，使最终达到最大堆的条件。例如

2 4 5 3 1

     2

  4    5

3  1

建立最大堆从4开始，4比1、3大，此步不动。

然后到2，从4、5中找大者5，2下移，5上移得出：

5 4 2 3 1

     5

  4   2

3  1

排序：

第一次找出最大值后为：

4 3 2 1 5

      4

  3      2

1  5

第二次找到最大值后为：

3 1 2 4 5

      3

  1      2

4  5
第三次找到最大值后为：

2 1 3 4 5

     2

 1     3

4 5

第四次找到最大值后为：

1 2 3 4 5

     1

  2    3

4  5

OK，排序完成。

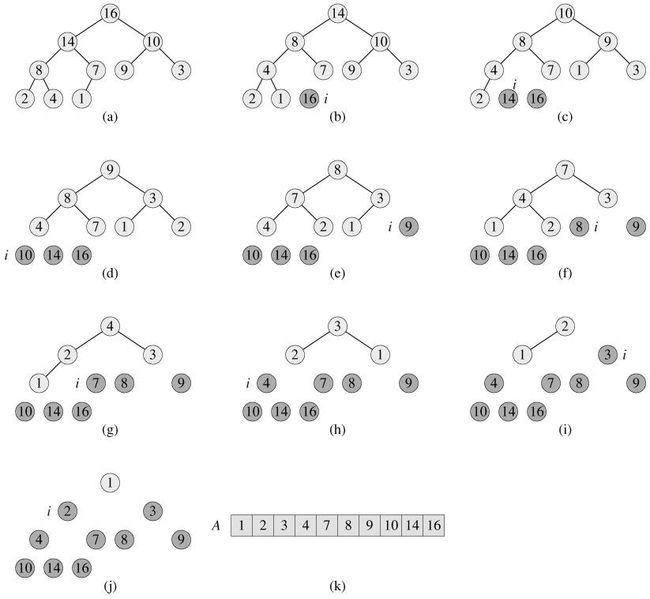
书中给出的一个例子：

建最大堆：

排序：

//堆排序，时间复杂度nlgn，原地排序
void HeapSort(int *pArray,int cnt);

#include "SK_Common.h"
#include "SK_Sort.h"

static inline int _Parent(int i)
{
    return (i+1)/2 - 1;
}

static inline int _Left(int i)
{
    return (i+1)*2 - 1;
}

static inline int _Right(int i)
{
    return (i+1)*2;
}

void _Max_HeapFy(int *pArray,int cnt,int pos)
{
    int maxpos = pos;
    int l = _Left(pos);
    int r = _Right(pos);
    if(l < cnt && pArray[l] > pArray[pos])
        maxpos = l;
    if(r < cnt && pArray[r] > pArray[maxpos])
        maxpos = r;

    if(maxpos != pos)
    {
        exchange(pArray+pos,pArray+maxpos);
        _Max_HeapFy(pArray,cnt,maxpos);
    }
}

void Make_Max_Heap(int *pArray,int cnt)
{
    int i = 0;
    for(i=_Parent(cnt);i>=0;i--)
    {
        _Max_HeapFy(pArray,cnt,i);
    }
}

void HeapSort(int *pArray,int cnt)
{
    if(cnt <= 1)
        return;
    int i = 0;
    Make_Max_Heap(pArray,cnt);

    for(i=cnt-1;i>0;i--)
    {
        exchange(pArray+i,pArray);
        _Max_HeapFy(pArray,i,0);
    }
}

堆排序不容易理解，几个过程都比较复杂，实际应用比较少。如果想深入学习，最好还是看一下算法导论的 第6章 堆排序。

本文只做简单介绍，均手打，简单贴图，具体贴图可参考《算法导论》的介绍。