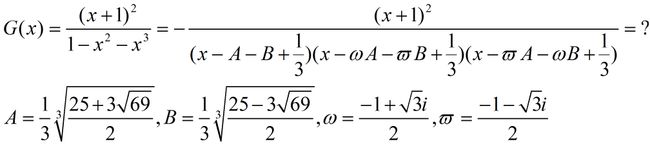UVa 11069 A Graph Problem (斐波那契)

11069 - A Graph Problem

Time limit: 3.000 seconds

http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=115&page=show_problem&problem=2010

Given an undirected graph of the following form with n nodes, 1 ≤ n ≤ 76: 

 

Your task is to calculate the number of subsets of nodes of the graph with the following properties:

• no nodes in the subset should be connected
• it shouldn't be possible to add further nodes to the subset without violating the first condition

For a graph with  5  nodes the number of subsets which fulfill the above conditions is 4 . The subsets are  {1,3,5},{2,4},{2,5},{1,4} .

Input

The input will consist of a sequence of numbers n,1 ≤ n ≤ 76. Each number will be on a separate line. The input will be terminated by EOF.

Output

Output the number of subsets as described above on a single line. The number of all subsets will be less than 2^31.

Sample input

1
2
3
4
5
30

Sample output

1
2
2
3
4
4410

思路：

注意到f(n)子集由 f(n-3)子集加上数n-1 与 f(n-2)子集加上数n 组成，所以有递推公式f[n]=f[n-3]+f[n-2]。

由于母函数分母是个三次多项式且因式分解很复杂，所以直接用递推公式就行。

完整代码：

/*0.015s*/

#include<cstdio>
using namespace std;
const int MAXN = 77;

int dp[MAXN];

int main()
{
	dp[1] = 1;
	dp[2] = 2;
	dp[3] = 2;
	for (int i = 4; i < MAXN; i++)
		dp[i] = dp[i - 3] + dp[i - 2];
	int n;
	while (~scanf("%d", &n))
		printf("%d\n", dp[n]);
	return 0;
}

打表：（居然变慢了。。这不科学）

/*0.019s*/

#include<cstdio>
using namespace std;
const int dp[77] = {0, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86,
					114, 151, 200, 265, 351, 465, 616, 816, 1081, 1432, 1897,
					2513, 3329, 4410, 5842, 7739, 10252, 13581, 17991, 23833,
					31572, 41824, 55405, 73396, 97229, 128801, 170625, 226030,
					299426, 396655, 525456, 696081, 922111, 1221537, 1618192,
					2143648, 2839729, 3761840, 4983377, 6601569, 8745217, 11584946,
					15346786, 20330163, 26931732, 35676949, 47261895, 62608681,
					82938844, 109870576, 145547525, 192809420, 255418101, 338356945,
					448227521, 593775046, 786584466, 1042002567, 1380359512, 1828587033
				   };

int main()
{
	int n;
	while (~scanf("%d", &n))
		printf("%d\n", dp[n]);
	return 0;
}

附上母函数：