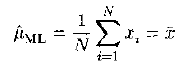协方差最大似然估计为什么比实际协方差小一点 E(ΣML)=(N-1)/N * Σ

我们都知道，给定N个一维实数空间上的样本点{ xi，i=1,2,3... }，假定样本点服从单峰高斯分布，那么，最大似然估计的参数表达式为：

期望：   方差：

可是，你是否注意过，在我们从小接受到的方差定义公式，却与最大似然估计的不一样，一个分母为n-1，一个为n。这是不是意味着最大似然估计的不准确？如何衡量这种不准确？换个角度，更进一步，方差的定义公式为什么要除以n-1？本文将从最后一个问题出发，一步一步解答这些问题。

本文主要以张贤达《现代信号处理》第二版第二章第一节为参考资料，辅以一些网页资料，并在文章中标注出引用处。

1、n-1能更准确的反应现实世界

如果样本集中只有一个样本，试问：这个时候高斯分布的方差应该是多少？是0还是无穷大？如果是无穷大，那么来第二个样本点的话，我们将是无法预知落在什么地方（方差无穷大，可以看做是整个实数轴上的均匀分布）；如果是0，那么来第二个样本点的话，我们将肯定它的值仍然等于x1（方差为零，可以看做是确定事件）。显然，方差为无穷大更符合现实世界，更符合我们的直观感受。也就是是说，分母为n-1更能反应现实世界。

这里还有另外一种直观的理解，但是难以自圆其说，来自http://blog.csdn.net/feliciafay/article/details/5878036。这里直接摘抄在这里，也很好理解，作者同时也给出了为什么这种直观的解释难以自圆其说。

“样本的容量小于整体，所以有较小的可能性抽中一些极端的数据。比如找来一堆人做样本来测量身高，那么样本中出现巨人的可能性是很小的，这样得到的结果可能就比实际小。为了弥补这点不足，就把分母变得小一些，这样就更能反应实际数据了。 质疑：这个解释其实不太合理。因为既然可能抽不到高个子，也同样可能抽不到矮个子，所以，分母既然可以变得小一些，也就应该有同样的理由变得大一些。我认为这个角度并不能说明问题。”

2、自由度的解释

这一点解释也是网上普遍存在的一种解释，当然也属于比较直观的理解。可以这么理解，在期望的定义中我们看到，分子有N个独立的变量，则会在分母上除以N，而方差的定义式中，均值已经限制了前面N个样本值只有N-1个是独立的，因为一旦知道了N-1个样本点，就可以结合均值计算出第N个样本点。所以，方差的定义式中分母除以了N-1.

质疑：为什么N-1个独立变量，就应该在分母上除以N-1呢？

3、数学语言的解释

首先，引入估计子性能评估的概念。我们知道，参数估计方法多种多样，常见的有最大似然估计、最大后验估计、贝叶斯估计、最小均方误差估计等，那么如何评价这些估计子的性能呢？由此引入无偏估计和渐进无偏估计的概念。

所谓无偏估计，反应了这样一个事实，对一个参数估计多次，得到多个估计值，这多个估计值的平均值能够很好的逼近参数的真实值。严谨的数学定义为：

                        注意：估计值的均值是样本集大小N的函数。

所谓渐进无偏估计，则考虑到了这样一个直观的事实，每次估计时，样本越多，估计越准确，因此，当我们手头上有足够多的样本时，评估一个估计子的性能时，就可以比较他们在样本集大小N趋向无穷大时与真实值的偏差。严谨的数学定义为：

注意：无偏估计子一定是渐进无偏的，但是渐进无偏的不一定是无偏的。

下面，我们从无偏估计的定义出发，证明均值和方差的定义式（虽然是定义式，但也是定义在特定样本集上的，本质上仍然是一种对真实值的估计）都是对真实值的无偏估计。

编辑公式实在是件费尽的事情，直接写在纸上了，可能看起来有点费尽，见谅见谅。

由此可见，均值和方差的定义式均是无偏估计子。另外，我们需要注意的是，有偏的渐进无偏估计子并不一定比无偏估计子差，这主要体现在实际计算的可行性（矩阵满秩等问题）、计算复杂度等问题上。

4、总结

从上面三个方面我们可以理解方差的定义式中为什么用n-1作为分母，同时，我们需要知道的是，最大似然估计虽然是有偏估计，但是由于其渐进无偏性，是一种广泛使用的参数估计方法。