图形图像处理－之－任意角度的高质量的快速的图像旋转

A:旋转原理和旋转公式:
  推导旋转公式：
             
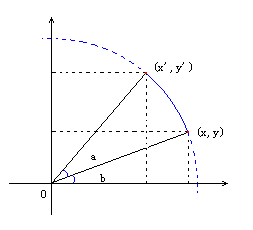
                       旋转示意图
   有：  tg(b)=y/x                             ----(1)
         tg(a+b)=y'/x'                         ----(2)
         x*x + y*y = x'*x' + y'*y'             ----(3)
   有公式：tg(a+b) = ( tg(a)+tg(b) ) / ( 1-tg(a)*tg(b) )  ----(4)
     把(1)代入(4)从而消除参数b;
     tg(a)+y/x = y'/x'*( 1-tg(a)*y/x )                ----(5)
     由(5)可以得x'=y'*(x-y*tg(a))/( x*tg(a)+y )       ----(6)
   把(6)代入(3)从而消除参数x',化简后求得:
     y'=x*sin(a)+y*cos(a);                     ----(7)
   把(7)代入(6),有:
     x'=x*cos(a)-y*sin(a);                     ----(8)

  OK，旋转公式有了，那么来看看在图片旋转中的应用；
  假设对图片上任意点(x,y)，绕一个坐标点(rx0,ry0)逆时针旋转RotaryAngle角度后的新的坐标设为(x', y')，有公式：
  (x平移rx0,y平移ry0,角度a对应-RotaryAngle ， 带入方程(7)、(8)后有： ) 
  x'= (x - rx0)*cos(RotaryAngle) + (y - ry0)*sin(RotaryAngle) + rx0 ;
  y'=-(x - rx0)*sin(RotaryAngle) + (y - ry0)*cos(RotaryAngle) + ry0 ;

那么，根据新的坐标点求源坐标点的公式为：
  x=(x'- rx0)*cos(RotaryAngle) - (y'- ry0)*sin(RotaryAngle) + rx0 ;
  y=(x'- rx0)*sin(RotaryAngle) + (y'- ry0)*cos(RotaryAngle) + ry0 ;

旋转的时候还可以顺便加入x轴和y轴的缩放和平移，而不影响速度，那么完整的公式为:           
  x=(x'- move_x-rx0)/ZoomX*cos(RotaryAngle) - (y'- move_y-ry0)/ZoomY*sin(RotaryAngle) + rx0 ;
  y=(x'- move_x-rx0)/ZoomX*sin(RotaryAngle) + (y'- move_y-ry0)/ZoomY*cos(RotaryAngle) + ry0 ;
  其中： RotaryAngle为逆时针旋转的角度;
         ZoomX,ZoomY为x轴y轴的缩放系数(支持负的系数,相当于图像翻转);
         move_x,move_y为x轴y轴的平移量;

一些颜色和图片的数据定义:

#define asm __asm

typedef unsigned  char TUInt8; // [0..255]
struct TARGB32      //32 bit color
{
    TUInt8  b,g,r,a;          //a is alpha
};

struct TPicRegion  //一块颜色数据区的描述，便于参数传递
{
    TARGB32*    pdata;         //颜色数据首地址
    long        byte_width;    // 一行数据的物理宽度(字节宽度)；
                //abs(byte_width)有可能大于等于width*sizeof(TARGB32);
    long        width;         //像素宽度
    long        height;        //像素高度
};

//那么访问一个点的函数可以写为：
inline TARGB32& Pixels(const TPicRegion& pic,const long x,const long  y)
{
    return ( (TARGB32*)((TUInt8*)pic.pdata+pic.byte_width* y) )[x];
}
//判断一个点是否在图片中
inline bool PixelsIsInPic(const TPicRegion& pic,const long x,const long  y)
{
    return ( (x>=0)&&(x<pic.width) && (y>=0)&&(y< pic.height) );
}

 

 B:一个简单的浮点实现版本

//////////////////////////////////////////////////////////////////////////////////////////////////////
//函数假设以原图片的中心点坐标为旋转和缩放的中心
void PicRotary0(const TPicRegion& Dst,const TPicRegion& Src,double RotaryAngle,double ZoomX,double ZoomY,double move_x,double  move_y)
{
    if ( (fabs(ZoomX*Src.width)<1.0e-4) || (fabs(ZoomY*Src.height)<1.0e-4) ) return; //太小的缩放比例认为已经不可见
    double rx0=Src.width*0.5;  //(rx0,ry0)为旋转中心 
    double ry0=Src.height*0.5 ; 
    for (long y=0;y<Dst.height;++ y)
    {
        for (long x=0;x<Dst.width;++ x)
        {
            long srcx=(long)((x- move_x-rx0)/ZoomX*cos(RotaryAngle) - (y- move_y-ry0)/ZoomY*sin(RotaryAngle) +  rx0) ;
            long srcy=(long)((x- move_x-rx0)/ZoomX*sin(RotaryAngle) + (y- move_y-ry0)/ZoomY*cos(RotaryAngle) +  ry0) ;
            if  (PixelsIsInPic(Src,srcx,srcy))
                Pixels(Dst,x,y)= Pixels(Src,srcx,srcy);
        }
    }
}

(调用方法比如:
   PicRotary0(ppicDst,ppicSrc,PI/6,0.9,0.9,(dst_wh-ppicSrc.width)*0.5,(dst_wh-ppicSrc.height)*0.5);
   //作用：将图片ppicSrc按0.9的缩放比例旋转PI/6幅度后绘制到图片ppicDst的中心
)

//注：测试图片都是800*600的图片旋转到1004*1004的图片中心 测试成绩取各个旋转角度的平均速度值
////////////////////////////////////////////////////////////////////////////////
//速度测试:                 
//==============================================================================
// PicRotary0              34.9 fps
//////////////////////////////////////////////////////////////////////////////// 

旋转结果图示（小图）：

   
                 30度                         60度                      90度

   
                 120度                       150度                      180度

  
                 210度                            240度                          270度

   
                 300度                        330度                       360度