排序算法(七)——堆排序
基本思想
堆排序是一种树形选择排序,是对直接选择排序的改进。
首先,我们来看看什么是堆(heap):
(1)堆中某个节点的值总是不大于或不小于其父节点的值;
(2)堆总是一棵完全二叉树(Complete Binary Tree)。
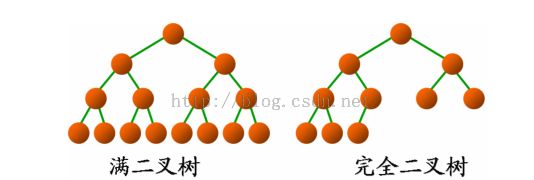
完全二叉树是由满二叉树(Full Binary Tree)而引出来的。除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树称为满二叉树。
如果除最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干结点,这样的二叉树被称为完全二叉树。
一棵完全二叉树,如果某个节点的值总是不大于其父节点的值,则根节点的关键字是所有节点关键字中最小的,称为小根堆(小顶堆);如果某个节点的值总是不小于其父节点的值,则根节点的关键字是所有节点关键字中最大的,称为大根堆(大顶堆)。
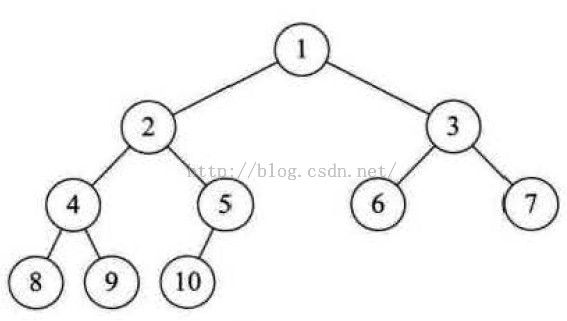
从根节点开始,按照每层从左到右的顺序对堆的节点进行编号:
可以发现,如果某个节点的编号为i,则它的子节点的编号分别为:2i、2i+1。据此,推出堆的数学定义:
具有n个元素的序列(k1,k2,...,kn),当且仅当满足
时称之为堆。
需要注意的是,堆只对父子节点做了约束,并没有对兄弟节点做任何约束,左子节点与右子节点没有必然的大小关系。
如果用数组存储堆中的数据,逻辑结构与存储结构如下:
初始时把要排序的n个数看作是一棵顺序存储的完全二叉树,调整它们的存储顺序,使之成为一个堆,将堆顶元素输出,得到n 个元素中最小(最大)的元素,这时堆的根节点的数最小(或者最大)。然后对前面(n-1)个元素重新调整使之成为堆,输出堆顶元素,得到n 个元素中次小(或次大)的元素。依次类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。这个过程就称为堆排序。
写代码之前,我们要解决一个问题:如何将一个不是堆的完全二叉树调整为堆。
例如我们要将这样一个无序序列:
49,38,65,97,76,13,27,49
建成堆,将它直接映射成二叉树,结果如下图的(a):
(a)是一个完全二叉树,但不是堆。我们将它调整为小顶堆。
堆有一个性质是:堆的每个子树也是堆。
调整的核心思想就是让树的每棵子树都成为堆,以某节点与它的左子节点、右子节点为操作单位,将三者中最小的元素置于子树的根上。
(a)中最后一个元素是49,在树中的序号为8,对应的数组下标则为7,它的父节点对应的数组下标为3(如果一个元素对应的存储数组的下标为i,则它的父节点对应的存储数组的下标为(i-1)/2),49小于97,所以两者交换位置。
此时,以第三层元素为根节点的所有子树都已是堆了,下一步继续调整以第二层元素为根节点的子树。
先调整以65为根的子树,再调整以38为根的子树(满足堆的要求,实际上不用调整)。
然后调整以第一层元素为根的子树,即以49为根,以38为左子节点,以13为右子节点的子树,交换13与49的位置。
一旦交换位置,就有可能影响本来已经是堆的子树。13与49交换位置之后,破坏了右子树,将焦点转移到49上面来,继续调整以它为根节点的子树。如果此次调整又影响了下一层的子树,继续调整,直至叶子节点。
以上就是由数组建堆的过程。
堆建好之后开始排序,堆顶就是最小值,取出放入数组中的最后一个位置,将堆底(数组中的最后一个元素)放入堆顶。这一操作会破坏堆,需要将前n-1个元素调整成堆。
然后再取出堆顶,放入数组的倒数第二个位置,堆底(数组中的倒数第二个元素)放入堆顶,再将前n-2个元素调整成堆。
按照上面的思路循环操作,最终就会将数组中的元素按降序的顺序排列完毕。
如果想要升序排列,利用大顶堆进行类似的操作即可。下面的java实现就是使用大顶堆完成的。
java实现
//堆排序 public void heapSort(){ buildHeap(); System.out.println("建堆:"); printTree(array.length); int lastIndex = array.length-1; while(lastIndex>0){ swap(0,lastIndex); //取出堆顶元素,将堆底放入堆顶。其实就是交换下标为0与lastIndex的数据 if(--lastIndex == 0) break; //只有一个元素时就不用调整堆了,排序结束 adjustHeap(0,lastIndex); //调整堆 System.out.println("调整堆:"); printTree(lastIndex+1); } } /** * 用数组中的元素建堆 */ private void buildHeap(){ int lastIndex = array.length-1; for(inti= (lastIndex-1)/2;i>=0;i--){ //(lastIndex-1)/2就是最后一个元素的根节点的下标,依次调整每棵子树 adjustHeap(i,lastIndex); //调整以下标i的元素为根的子树 } } /** * 调整以下标是rootIndex的元素为根的子树 *@param rootIndex 根的下标 *@param lastIndex 堆中最后一个元素的下标 */ private void adjustHeap(int rootIndex,intlastIndex){ int biggerIndex = rootIndex; int leftChildIndex = 2*rootIndex+1; int rightChildIndex = 2*rootIndex+2; if(rightChildIndex<=lastIndex){ //存在右子节点,则必存在左子节点 if(array[rootIndex]<array[leftChildIndex] || array[rootIndex]<array[rightChildIndex]){ //子节点中存在比根更大的元素 biggerIndex = array[leftChildIndex]<array[rightChildIndex] ? rightChildIndex :leftChildIndex; } }else if(leftChildIndex<=lastIndex){ //只存在左子节点 if(array[leftChildIndex]>array[rootIndex]){ //左子节点更大 biggerIndex = leftChildIndex; } } if(biggerIndex != rootIndex){ //找到了比根更大的子节点 swap(rootIndex,biggerIndex); //交换位置后可能会破坏子树,将焦点转向交换了位置的子节点,调整以它为根的子树 adjustHeap(biggerIndex,lastIndex); } } /** * 将数组按照完全二叉树的形式打印出来 */ private void printTree(int len){ int layers = (int)Math.floor(Math.log((double)len)/Math.log((double)2))+1; //树的层数 int maxWidth = (int)Math.pow(2,layers)-1; //树的最大宽度 int endSpacing = maxWidth; int spacing; int numberOfThisLayer; for(int i=1;i<=layers;i++){ //从第一层开始,逐层打印 endSpacing = endSpacing/2; //每层打印之前需要打印的空格数 spacing = 2*endSpacing+1; //元素之间应该打印的空格数 numberOfThisLayer = (int)Math.pow(2, i-1); //该层要打印的元素总数 int j; for(j=0;j<endSpacing;j++){ System.out.print(" "); } int beginIndex = (int)Math.pow(2,i-1)-1; //该层第一个元素对应的数组下标 for(j=1;j<=numberOfThisLayer;j++){ System.out.print(array[beginIndex++]+""); for(intk=0;k<spacing;k++){ //打印元素之间的空格 System.out.print(" "); } if(beginIndex == len){ //已打印到最后一个元素 break; } } System.out.println(); } System.out.println(); }用以下代码测试:
int [] a = {7,1,9,2,5,10,6,4,3,8}; Sort sort = new Sort(a); System.out.println("未排序时:"); sort.display(); System.out.println(); sort.heapSort(); System.out.println("排序完成:"); sort.display();打印结果如下:
算法分析
它的运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个结点到根结点的距离为log2i+1),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
所以总体来说,堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n2)的时间复杂度了。
空间复杂度上,它只有一个用来交换的暂存单元,也非常的不错。不过由于记录的比较与交换是跳跃式进行,因此堆排序是一种不稳定的排序方法。