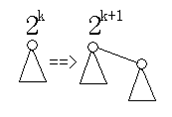可并堆与二叉堆

比较实用的堆有二叉堆（完全二叉树），因为其空间需求最小（可用数组实现），编程复杂度最低。

但是，在特殊情况时，需要常用合并操作并且n较大时，二叉堆的合并操作的复杂度是o（n），如果n是较大的值，可能是比较难以接受的，所以就有了可并堆。

本文主要学习可并堆的理论上的知识点。

1、二叉堆

定义：

二叉堆满足堆特性：

1）父结点的键值总是大于或等于（小于或等于）任何一个子结点的键值，且每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）

2）完全二叉树,结点i的儿子是2*i+1和2*i+2，父亲是i/2（下标从0开始）;

3）当且仅当它满足以下两个条件之一时，才能称之为堆：

3-1)a[i]<=a[i*2+1]且a[i]<=a[i*2+2](即小根堆，节点的值不大于两个儿子的值)

3-2)a[i]>=a[i*2+1]且a[i]>=a[i*2+2](即大根堆，节点的值不小于两个儿子的值)

各种操作的时间复杂度

1）构建O(n)

2）插入O(logn)

3）取最小结点O(1)

4）删除最小结点O(logn)

5）删除任意结点O(logn)

6）合并O(n)

2、可并堆

定义

1)可并堆(Mergeable Heap)也是一种抽象数据类型，它除了支持优先队列的三个基本操作(Insert, Minimum, Delete-Min)，

还支持一个额外的操作——合并操作：

2)H ← Merge(H1,H2)

Merge() 构造并返回一个包含H1和H2所有元素的新堆H。

各种可并堆：

(1)斜堆(SkewHeap)

(2)左偏树(LeftistTree)

(3)二项堆(BinomialHeap)

(4)配对堆(PairingHeap)

(5)斐波那契堆(FibonacciHeap)

各种操作的复杂度比较：

(1)斜堆（ SkewHeap）

满足堆性质：

(1)父结点的键值总是大于或等于（小于或等于）任何一个子结点的键值

(2)每个结点的左子树和右子树都是斜堆

(3)结构看起来与普通的二叉树类似

合并A，B链两个斜堆

合并操作：merge( A, B)

(1)将以A，B为根结点的两个斜堆合并，再返回合并后的新斜堆的根结点。

(2)小根堆为例：

假设A.key <=B.key就将A的右子树与B合并(递归进行)当做A的新的右子树。然后交换A的左右子树。

(3)斜堆的插入\删除操作都是建立在合并操作的基础上的。

1）插入: 

将待插入的结点当做是一个只有一个结点的斜堆，用merge()将它合并到原斜堆

2）删除: 

将要删除的结点的左右儿子合并即可

小根堆合并伪代码:

Struct Node
{
  int key,lch,rch;//值，左节点索引，右节点索引
}
..merge(A,B)
{
  if (A == NULL) return B;
  if (B == NULL) return A;
  if (A.key > B.key)swap(A,B);//如果A的值较大，则交换A和B节点
  A.rch = merge(A.rch,B);//把A的右子树与B合并(递归进行)当做A的新的右子树
  swap(A.rch,A.lch);//交换A的左右子树
  return A;
}

复杂度

(1)由于没有对斜堆的右子树的深度做限制,因此最坏情况下复杂度为O(N)

(2)其均摊复杂度为O(logN),且有证明不超过为O(4logN)，

具体证明参考《Data Structure and ProblemSolving Using Java Second Edition》（Mark Allen Weiss 著,电子工业出版社出版）中的784页的Theorem23.2。

而且实践证明其效果还是不错的…

（3）Insert() Delete() 中都只调用了一次merge()因此他们的复杂度与merge()相同

 （2）左偏树(LeftistTree)

结构图如下：

基本结构:

与斜堆一样，只是左偏树的每个结点多了一个距离值NPL(Null Path Length)即该结点一直向右儿子走，到达空结点的距离。

时间复杂度

（1）NPL值的引入能保证树左偏，使之不会退化成斜堆那样的最坏情况，保证了的最坏情况下的效率

（2）由于每次merge 时都是将一棵树的右子树和另一棵树合并，利用NPL值能保证分解的次数不会超过log(N1+1) + log(N2+1) -2，

其中N1和N2分别为左偏树A和B的结点个数，因此最坏情况下的时间复杂度为O(log N1 + log N2)。

具体参见http://wenku.baidu.com/view/20e9ff18964bcf84b9d57ba1.html

合并操作，伪代码

Merge(A, B)
{
  If (A== NULL) return B;
  If (B== NULL) return A;
  If key[B] < key[A] Then swap(A, B);
  rch[A]  = Merge(rch[A],B);
  If ( NPL[ rch[A] ] > NPL[ lch[A] ] )//一直向右儿子走，到达空结点的距离的值的比较
  swap( lch[A], rch[A]);
  NPL[A] = NPL[rch[A]] + 1;//Merge操作时维护NPL的值
  return A
}

（3）二项堆(BinomialHeap)

定义：

二项堆是二项树的森林

二项树：节点数为2k，k=0,1,2,3……，如下图

定义：Bk是有2k个结点的二项树

则：Bk+1 = Bk+Bk

二项树->二项堆

（1）有n个结点的二项堆：

如n = 13，表示成:

2k形式的和,如13 =2的0次幂+2的2次幂+2的3次幂 =1+4+8

分别将Bk按k递增顺序连起来，组成一个树根链表，如13个结点的二项堆,将B0，B2，B3的根结点连起来：

二项树增加结点

时间复杂度

（1）找堆中的最小值：

遍历树根链表即可。最坏时间复杂度：O(log n)

（2）合并操作Merge()：

基本原理类似二进制加法。最坏情况下时间复杂度：O(log n)

 

实现方式:用左儿子右兄弟的方法存储树。更多操作及具体实现：《算法导论》

（4）配对堆(PairingHeap)

操作的时间复杂度:

参考维基百科 http://en.wikipedia.org/wiki/Pairing_heap

简单介绍

(1)配对堆是棵多叉树，满足堆性质；

(2)以左儿子右兄弟的方式存贮树

(3)仅简单介绍Merge()原理 ：

以小根堆为例，比较两根的值，以较小的根作为结果的根，较大的根变成结果的根的子树。

当黑key < 白key 时，组合如下

Pairing Heap参考代码(排序)：

#include <iostream>
#include <ctime>

using namespace std;

struct node
{
int value;
node *ch[2], *pre;
} tree[1000001], *tmp[1000001], *root, *Null;

int top = 0;

node *New_Node(int x)
{
node *p = &tree[top ++];
p->value = x, p->ch[0] = p->ch[1] = p->pre = Null;
return p;
}

node *Link(node *a, node *b)
{
if (a->value > b->value) swap(a, b);
if (b == Null) return a;
b->ch[1] = a->ch[0];
if (a->ch[0] != Null) a->ch[0]->pre = b;
a->ch[0] = b, b->pre = a;
return a;
}

node *Combine(node *x)
{
int total = 0, i;
node *y, *z, *res;
if (x == Null) return Null;
for ( ; x != Null; x = z)
{
y = x->ch[1], z = y->ch[1];
x->ch[1] = y->ch[1] = y->pre = z->pre = Null;
tmp[++ total] = Link(x, y);
}
for (res = tmp[total], i = total-1; i; i --)
res = Link(res, tmp[i]);
return res;
}

int main()
{
int n, i;

freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);

root = Null = New_Node(INT_MAX);
Null->ch[0] = Null->ch[1] = Null->pre = Null;
scanf("%d", &n), srand(time(0));
for (i = 1; i <= n; i ++)
root = Link(root, New_Node((rand()<<16)+rand()));
for (i = 1; i <= n; i ++)
printf("%d ", root->value), root = Combine(root->ch[0]);
printf("\n");

return 0;
}

（5）斐波那契堆(FibonacciHeap)

操作时间复杂度

参考：http://en.wikipedia.org/wiki/Fibonacci_Heap

简单介绍

（1）一个斐波那契堆由多个子树构成，并将子树的根结点连接成双向链表，并由一个min指向其中的最小的结点。

（2）每个子树都是多叉树，且每个结点的所有儿子连成双向链表，每个儿子都有指向父亲的指针，但父亲只有指向其儿子中key最小的那个儿子的指针。

Merge()

1） 根据斐波那契堆的结构特点，可以很清楚的看到，合并两个堆只要将各自的根表合并，在让 min 指向各自的 min 中的较小者

2）对根表中的子树进行合并是必须的，但这个操作被放在抽取最小结点中进行。

更多具体操作可见《算法导论》第20章