多源最短路径--Floyd-Warshall算法

任意两点最短路径被称为多源最短路径，即给定任意两个点，一个出发点，一个到达点，求这两个点的之间的最短路径，就是任意两点最短路径问题，多源最短路径，而Floyd-Warshall算法最简单，只有5行代码，即可解决这个问题。

上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题被称为“多源最短路径”问题。


现在需要一个邻接矩阵来存储图的信息，在这里我们可以用一个4*4的矩阵（二维数组e）来存储。比如1号城市到2号城市的路程为2，则设e[1][2]的值为2。2号城市无法到达4号城市，则设置e[2][4]的值为∞。另外此处约定一个城市自己是到自己的也是0，例如e[1][1]为0，具体如下：

我们来想一想，根据我们以往的经验，如果要让任意两点（例如从顶点a点到顶点b）之间的路程变短，只能引入第三个点（顶点k），并通过这个顶点k中转即a->k->b，才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢？甚至有时候不只通过一个点，而是经过两个点或者更多点中转会更短，即a->k1->k2->b或者a->k1->k2…->ki->…->b。比如上图中从4号城市到3号城市（4->3）的路程e[4][3]原本是12。如果只通过1号城市中转（4->1->3），路程将缩短为11（e[4][1]+e[1][3]=5+6=11）。其实1号城市到3号城市也可以通过2号城市中转，使得1号到3号城市的路程缩短为5（e[1][2]+e[2][3]=2+3=5）。所以如果同时经过1号和2号两个城市中转的话，从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子，我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。好，这个过程只需要5句代码来实现：

//Floyd-Warshall算法
	for (int k = 0; k < vertexNum; k++)
		for (int i = 0; i < vertexNum; i++)
			for (int j = 0; j < vertexNum; j++)
				if (matrix[i][j]>matrix[i][k] + matrix[k][j])
					matrix[i][j] = matrix[i][k] + matrix[k][j];

如果学过单源最短路径，那么多源最短路径应该是很简单的。这里需要注意的是上述算法的k,i,j顺序是不可以颠倒的。因为在这句算法“ matrix[i][j] = matrix[i][k] + matrix[k][j] ”成立的一个隐藏前提是matrix[i][k]和matrix[k][j]必须是最小，因此k是必须放在第一个循环中。

另外一个注意点Floyd-Warshall算法可以解决负权图，但是不可以解决“负权回路”（或者叫“负权环”）的图。因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中，每绕一次1->-2>3这样的环，最短路就会减少1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。见下图：

下面贴上完整代码：

#include<iostream>  
#include<iomanip>

#define INF 10001//假设权值不大于100

using namespace std;


int matrix[10][10];//假设不超过10个顶点，邻接矩阵存储


int main()
{
/*

4 8

0 1 2
0 2 6
0 3 4
1 2 3
2 0 7
2 3 1
3 0 5
3 2 12

*/
	for (int i = 0; i < 10; i++)//初始化
	{
		for (int j = 0; j < 10; j++)
		{
			if (i == j)
				matrix[i][j] = 0;
			else
				matrix[i][j] = INF;
		}
	}

	int vertexNum, sideNum;//顶点数和边数
	int x, y, w;//边的信息和权值

	cout << "请输入顶点数和边数： ";
	cin >> vertexNum >> sideNum;

	cout << "\n请输入" << sideNum << "条边的信息和权值:\n";
	for (int i = 0; i < sideNum; i++)
	{
		cin >> x >> y >> w;
		matrix[x][y] = w;//有向图
	}

	//Floyd-Warshall算法
	for (int k = 0; k < vertexNum; k++)
		for (int i = 0; i < vertexNum; i++)
			for (int j = 0; j < vertexNum; j++)
				if (matrix[i][j]>matrix[i][k] + matrix[k][j])
					matrix[i][j] = matrix[i][k] + matrix[k][j];

	//输出结果
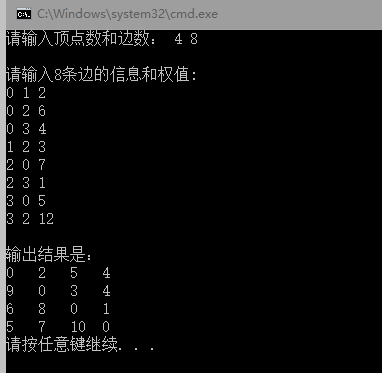
	cout << "\n输出结果是：\n";
	for (int i = 0; i < vertexNum; i++)
	{
		for (int j = 0; j < vertexNum; j++)
			cout << left << setw(4) << matrix[i][j];
		cout << endl;
	}


	
	return 0;
}

输出结果是：

图片资源来自：http://blog.csdn.net/turingbooks/article/details/28635933