Altera OpenCL用于计算机领域的13个经典案例

英文出自：Streamcomputing

转自：http://www.csdn.net/article/2013-10-29/2817319-the-application-areas-opencl-can-be-used

摘要：当使用加速器和OpenCL时，哪种类型的算法更加快速？来自弗吉尼亚理工大学的Wu Feng教授和他的团队例举了一份算法列表，分享了OpenCL常被用于计算机领域的13个经典案例。 有人将其称之为OpenCL计算领域的13个"小巨人"。

一、Dense Linear Algebra（稠密线性代数）

经典的向量和矩阵运算，传统上可分为1级（矢量/矢量vector/vector），2级（矩阵/矢量），3级（矩阵/矩阵），应用范围极其广泛。

应用范围：

• 线性代数：LAPACK， ATLAS。
• Clustering algorithms （聚类算法）/ Data-mining（数据挖掘）：StreamCluster， K-均值算法。

正常情况下执行循环，但大多数情况下可轻易在OpenCL进行并行计算。

二、Sparse Linear Algebra（稀疏线性代数）

乘法运算主要是由零矩阵组成。通过移动对角矩阵周围的非零元素，使计算更加高效。

应用范围：

• 有限元素分析。
• 偏微分方程式。

使用OpenCL有两种方法：通过一些列的操作行为解决该问题，这将导致很大一部分开销；第二种方法是使用一些列连续的逐次逼近法，将函数误差最小化。

三、Spectral Methods（光谱法）

各种结构的物质都具有自己的特征光谱，光谱分析法就是利用特征光谱研究物质结构或测定化学成分的方法。

光谱方法可用来解决常微分方程（ODEs），偏微分方程（PDEs）以及包含微分方程增值问题。

应用范围：

• 流体动力学。
• 量子力学。
• 天气预测。

利用OpenCL针对每个硬件架构有各种FFT实施方法。诀窍是调优。

四、N-Body Methods

N-Body法是模拟粒子的动力学系统，通常在物理学的影响下如重力，计算方法有两种（A影响B，同样B也影响A），整个系统在每一轮之后都会再次更新。

基本算法是O(N^2)。对于大型系统的优化，可以通过neighbour-administration（相邻管理）和远离粒子计算，这里运行时方法是可取的。

应用范围：

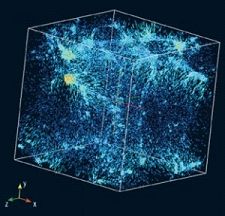
• 天文学：宇宙学（比如，星系的形成）。
• 计算化学：分子动力学（比如蛋白质折叠），分子模拟。
• 物理：流体动力学，等离子体物理学。

OpenCL可以实现每秒数以万计的粒子。

五、Structured Grids（结构化网格）

结构化网格是指网格区域内所有的内部点都具有相同的毗邻单元。在一个结构化或规则的网格中所有的元素具有相同的尺寸，比如方形模块。计算方法依赖于相邻的不规则网格。

应用范围：

• 图形处理：Gaussian image blurring 高斯图像模糊。
• Physics Simulations：transient thermal differential equation solver。
• Finite Element Method（有限元素法）。

利用OpenCL，网格有规则，因此映射也相当容易。要解决的问题是如何做到相邻网格之间的连通性。

六、Unstructured Grids（非结构化网格）

所有的网格都无规则性，不同的元素有着不同的相邻数量。这一组有很多的重叠与回溯。网格中的每个元素都可以是二维的多边形或者三维多面体。每个元素之间没有隐含的连通性。

应用范围：

• 计算流体动力学。
• Belief propagation（置信传播）。

难点是在硬件上映射不规则网格。

七、Map-Reduce & Monte Carlo

每个进程可独立于其他进程运行，因此，在相邻的进程之间没有连通性。在庞大的数据集和计算密集型算法中，GPU可结合大数据解决方法，比如Hadoop。

应用范围：

• Monte-Carlo（蒙特卡洛法）：PI（圆周率）计算法，碰撞仿真，序列对比。
• 分布式搜索。

由于节点之间的通信是最小的，这也是使用GPU最快的方法之一。

八、Combinational Logic（组合逻辑）

组合逻辑电路是一种逻辑电路，它的任一时刻的稳态输出，仅仅与该时刻的输入变量的取值有关，而与该时刻以前的输入变量取值无关。该算法中涉及大量的数据，可利用位级操作（ bit-level ）执行简单的操作。

应用范围：

• Computing checksums。
• 计算校验法，CRCs。
• 加密和解密。
• 散列。
• Hamming weight。

并不是所有的硬件都适合这种类型的操作，因此，设备的选择是至关重要的。

九、Graph Traversal（图形追踪）

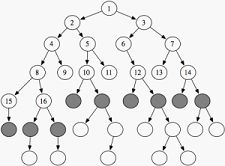
图形追踪是以特定的方式访问所有节点，更新/检查值。树形追踪是属于图形追踪一种特殊情况，有间接查找和微计算。

应用范围：

• 搜索：深度优先搜索，广度优先搜索，找到所有节点中某个连接组件。
• 排序：快速排序。
• 序列化/反序列化。
• Maze生成。
• 碰撞检测。

使用OpenCL，最关键的是要保持核心程序处于繁忙状态。

十、Dynamic Programming（动态规划）

它是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

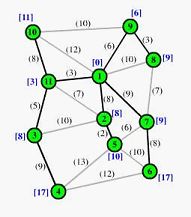动态规划常适用于解决简单的重叠子问题和最优子结构性质的问题。许多动态编程问题操作通过在网格中填写具有代表性的问题领域，这个领域在网格中保留着最终答案。

应用范围：

• 图形问题：Floyd's AllPairs，最短路径， Bellman-Ford算法。
• 序列对比：Needleman-Wunsch, Smith-Waterman。

"动态"应用，在运行时进行调优以达到最佳性能。

十一、Backtracking（回溯法）

回溯法（探索与回溯法）是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为"回溯点"。

这组通用的解决方法是分支定界（分而治之）。

应用范围：

• 智力游戏：N-queens，填字游戏，九宫格游戏，Peg接龙。
• Travelling salesman（旅行推销员）。
• Knapsack，子集和问题以及分区问题。
• 整数线性规划。
• Boolean Satisfiability（布尔运算）。
• Combinatorial Optimisation（组合优化）。

在OpenCL中最重要的就是避免大的分支。

十二、Probabilistic Graphical Models（概率图模型）

这个图形结合了不确定性（概率）和逻辑结构（独立约束）表示复杂的、现实世界的现象。

应用范围：

• Bayesian（贝叶斯）网络：信念网络，概念网络，因果网络，知识地图。
• Hidden Markov models（隐马尔可夫模型）。
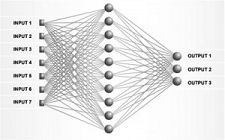
• Neural networks。

随着越来越多的进程需要更新相同的节点（原子学就是典型的案例），因此，需消耗大量的时间。

十三、Finite State Machines（有限状态机）

有限状态机是指有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

其具有三个特征：状态总数（state）是有限的；任一时刻，只处在一种状态之中；某种条件下，会从一种状态转变（transition）到另一种状态。

数学计算模型常用于设计连接计算机程序和时序逻辑电路。它常被看作是一个抽象性的机器，可用在有限的数量状态下。

应用范围：

• 视频解码，解析，压缩。
• 数据挖掘。

查找循环模式。