我们聊聊快排吧...

最近一直在看《编程珠玑》第二版这一本书，里面的东西真的很实用，以前也看过不少讲解快排的书，但是在编程珠玑上看到的讲解是我见过最好理解，也是最详细的，从效率和空间以及实现等各个方面都做了详细说明，并比较了几种变形的快排的效率，所以在这mark一下，留着以后忘了的时候看。

1.1.插入排序

首先说一下插入排序，这个会在最后的变形快排中用到，插入排序类似于整理扑克牌的方式，假设之前的序列已经有序，当拿到一个新的数字的时候，只要将其插入到之前的合适位置即可，知道所有数据都被处理完，整个数列就有序了。伪代码如下：

1 insort()
2 {
3     for i = [1,n)
4         for(j = i; j > 0 && x[j - 1] > x[j]; j--)
5             swap(x[j-1],j)
6 }

1.2.最简单的快排程序

还是说一下快排的基本原理吧，快排的思想基于分治法，首先将数组分成两个小部分，使数组的前一部分值都小于某一个哨兵值t，后半部分都大于t，然后再递归的进行快排这两个子数组，直到数组的元素只剩下一个。在最简单的快排中这样的哨兵值设置为字数组中的第一个值x[l].

最简单的快排划分数组部分的伪代码如下:

1 m = l
2 for i = [l,u]
3     if x[i] < t
4         swap(x[++m],x[i])

下面利用图示来进行讲解，这样更直观。

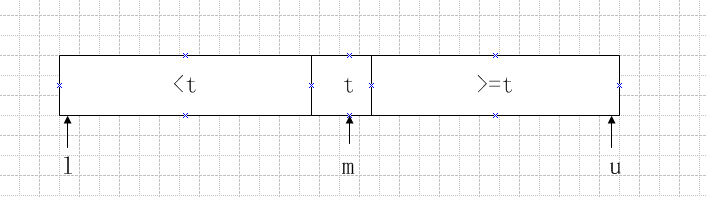
如上图所示，假设这是进行了几次简单快排后的数组的状态,当扫描位置到位置 i 时，如果x[i] < 哨兵值x[l]则需要交换m的下一个位置和位置i的值，m的下一个位置指向的是第一个比哨兵值x[l]大的位置.

 

当循环终止的时候情况如下:

如上图所示此时整个数组的所有元素都已经划分好了，此时m指向的是最后一个比t小的元素的位置，所以只需要交换一下哨兵位置和m位置的值就得到了数组的有序序列，如下图所示。

下面附上简单快排程序的完整的代码:

 1 void qsort1(int l,int u)
 2 {
 3     if(l >= u)
 4     {
 5         return;
 6     }
 7 
 8     int i,m = l;
 9     for(i = l + 1; i <= u, i++)
10     {
11         if(x[i] < x[l])
12         {
13             swap(x[++m],x[i]);
14         }
15     }
16 
17     swap(l,m);
18 
19     qsort1(l,m - 1);
20     qsort1(m + 1,u);
21 }

1.3.双向划分的快排程序

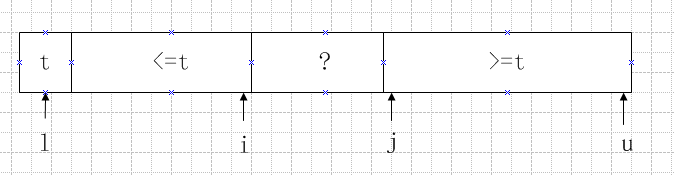
      双向划分就是设置两个游标分别从数组的左侧，和右侧开始，左侧每次找到比哨兵值t(现在为x[0])大的位置，右侧每次找到比哨兵值t小的位置，如果两个下标没有交叉就交换他们的值，直到，两个游标产生交叉。这种思想可以避免在数组中所有元素都相同时产生平方时间的算法，而是比较差不多n*logn的次数即可，同时可以减少总的比较次数。

双向划分的图示如下：

 

双向划分的快排程序的代码如下：

 

 1 void qsort2(int l,int u)
 2 {
 3     if(l >= u)
 4     {
 5         return ;
 6     }
 7 
 8     int t = x[l],i = l,j = u + 1;
 9     
10     while(1)
11     {
12         while(i <= u && x[i] < t)
13         {//find first bigger than t position from start
14             i++;
15         }
16 
17         while(x[j] > t)
18         {//find first smaller than t postin from end
19             j--;
20         }
21 
22         if(i > j)
23         {
24             break ;
25         }
26         
27         swap(x[i],x[j]);
28     }
29 
30     swap(x[l],x[j]);
31 
32     qsort2(l,j - 1);
33     qsort2(j + 1,u);
34 }

 

1.4.哨兵随机，小数组不处理快排

    当数组已经按升序排好序时，会导致快排是o(n2)时间复杂度的，所以使用哨兵值随机划分，可以避免这种情况，方法是把x[l]和x[l..u]中的一个随机项来进行交换，然后在设置x[l]为划分数组哨兵值，实现函数为swap(x[l],x[rand(l,u)])。

　　而且当快排进行划分到每个子数组很小时，原来的快排程序花费了大量的时间来排序这小很小的子数组，如果这时用1.1中所介绍的插入排序来排序数组会非常有效，因为当用快排排序到后面的小数组阶段时，数组已经基本有序了，而插入排序对基本有序的数组排序是非常快的，在《编程珠玑》第二版这本书中，作者做了实验，验证出这个小数组的值边界设置为50时，然后再调用插入排序，变形过得快排程序处理最快。

 　　代码如下：

 1 #define SAMLL_CUTOFF 50
 2 
 3 void qsort3(int l,int u)
 4 {
 5     if(u - l < SMALL_CUTOFF)
 6     {//剩下的小数组的时候结束快排,防止对小数组进行大量排序
 7         return;
 8     }
 9 
10     swap(x[l],x[rand(l,u)]);
11     
12     int t = x[l],i = l,j = u + 1;
13     while(1)
14     {
15         while(i <= u && x[i] < t)
16         {
17             i++;
18         }
19 
20         while(x[j] < t)
21         {
22             j--;
23         }
24 
25         if(i > j)
26         {
27             break;
28         }
29         
30         swap(x[i],x[j]);
31     }
32 
33     swap(x[l],x[j]);
34 
35     qsort3(l,j - 1);
36     qsort3(j + 1,u);
37 }

对该快排函数调用时方式如下：

1 qsort3(0,n-1);
2 insort();

 

1.5.作者进行了效率对比如下表：

程序	时间(纳秒)
C库函数qsort	137n logn
qsort1	60 n logn
qsort2	44n logn
qsort3	36n logn
C++库函数sort	30n logn

 

 

 

 

 

 

 

 l

 

 1.6.线性选择问题（选出数组中第k小的元素）

线性选择问题可以基于堆排序或者快排做，以前在计算机算法设计与分析那本书上看过这个问题，就放在这里一起记录吧。

解决思路：

由于每次快排将元素分为左右两部分，左边都比哨兵值小，右边都比哨兵值大，所以可以基于这个特性，在每次快排后对哨兵最后交换的位置m进行判断，如果m比k大说明第k小的元素在左边，只需在左边子数组继续边递归找第k小的元素即可，如果m比k小大则说明第k小的值在右边，则需要在右边子数组中找第k-m小的元素(由于左侧的m个元素都比k小)，知道递归结束后返回x[k-1]（因为数组下标从0开始）即可。

基于快排的线性选择代码如下：

 1 void kth_select(int l,int u,int k)
 2 {
 3     if(l >= u)
 4     {
 5         return ;
 6     }
 7 
 8     swap(l,rand(l,u));
 9     
10     int t = x[l],i = l,j = u + 1;
11     
12     while(1)
13     {
14         while(i <= u && x[i] < t)
15         {
16             i++;
17         }
18 
19         while(x[j] > t)
20         {
21             j--;
22         }
23 
24         if(i > j)
25         {
26             break ;
27         }
28 
29         swap(x[i],x[j]);
30     }
31 
32     swap(x[l],x[j]);
33 
34     if(j < k)
35     {//第k个元素在右侧，继续在右侧找第k-j个元素
36         kth_select(j + 1,u,k - j);
37     }
38     else if(j > k)
39     {
40         kth_select(l,j - 1,k);
41     }
42 }

该函数的调用如下，kth_select(0,u - 1,k-1);(数组下标从0开始)