【模式匹配】Aho-Corasick自动机

1. 多模匹配

AC自动机（Aho-Corasick Automaton）是多模匹配算法的一种。所谓多模匹配，是指在字符串匹配中，模式串有多个。前面所介绍的KMP、BM为单模匹配，即模式串只有一个。假设主串\(T[1 \cdots m]\)，模式串有k个\(\mathbb{P} = \{ P_1, \cdots, P_k\}\)，且模式串集合的总长度为\(n\)。如果采用KMP来匹配多模式串，则算法复杂度为：

\[ O(|P_1|+m+\cdots + |P_k|+m)=O(n+km) \]

而KMP并没有利用到模式串之间的重复字符结构信息，每一次的匹配都需要将主串从头至尾扫描一遍。因此，贝尔实验室的Aho与Corasick于1975年结合KMP与有限状态机（finite state machines）的思想，提出AC自动机算法[1]。

2. AC算法

AC自动机

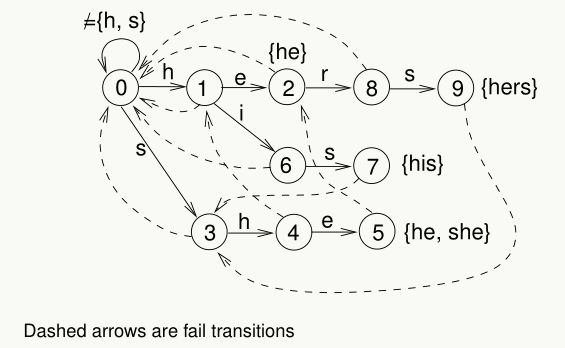
自动机由状态（数字标记的圆圈）和转换（带标签的箭头）组成，每一次转换对应一个字符。AC算法的核心包括三个函数：goto、failure、output；这三个函数构成了AC自动机。对于模式串{he, his, hers, she}，goto函数表示字符按模式串的转移，暗含了模式串的重复字符结构信息，如下图：

failure函数表示转移失败时退回的状态：

output函数表示模式串对应于自动机的状态：

完整的AC自动机如下：

匹配

AC算法根据自动机匹配模式串，过程比较简单：从主串的首字符、自动机的初始状态0开始，

• 若字符匹配成功，则按自动机的goto函数转移到下一状态；且若转移的状态对应有output函数，则输出已匹配上的模式串；
• 若字符匹配失败，则按自动机的failure函数进行转移

构造

AC自动机的确简单高效，但是如何构造其对应的goto、failure、output函数呢？首先来看goto函数，细心一点我们发现goto函数本质上就是一颗trie树，利用模式串的共同前缀信息；其与output函数共同表示模式串的字符结构的信息。

failure函数是整个AC算法的精妙之处，其构造过程不复杂，利用到了一个简单的规律：当匹配失败时，其回溯的状态应为前一状态的failure函数所转移的状态按前一字符goto到的状态，或前一状态的前一状态的failure函数所转移的状态按前一字符goto到的状态...上面的话听着有点拗口，我们看看上图AC自动机的例子：

• 当状态7转移失败时，前一状态6的failure函数转移的状态为0，状态0按前一字符s可以goto到状态3，所以状态7的failure函数\(f(7)=3\)；
• 当状态2转移失败时，前一状态1的failure函数转移的状态为0，状态0按前一字符e不可以goto任何状态，所以状态2的failure函数\(f(2)=0\)；

我们用\(g(r,a)=s\)表示状态r可以按字符a goto到状态s。根据goto表（trie树）的特性，可知某一状态的前一状态是唯一确定的，因此定义\(g^{-1}(s)=r\)表示状态s的前一状态为r；\(c^{-1}(s)=a\)表示状态s的前一转移字符为a。那么，状态s的failure函数可定义为：

\[ f(s) = \left \{ {\matrix { {g^{-n}(s)} & \min_{n} g(g^{-n},c^{-n})\neq failure\cr {0} & else \cr }}\right. \]

直观分析过程看似简单，但计算failure函数有小技巧——巧妙地运用了队列，具体实现如下：

Talk is cheap, show me the code. Java实现请参看这里

3. 参考资料

[1] Alfred V. Aho and Margaret J. Corasick, "String Matching: An Aid to Bibliographic Search".
[2] Pekka Kilpeläinen, Lecture 4: Set Matching and Aho-Corasick Algorithm.