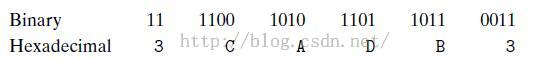深入理解计算机系统 2.1.1 十六进制记法

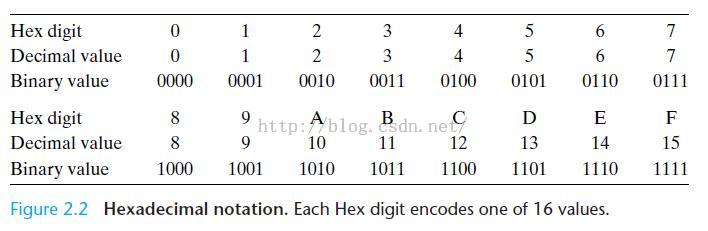
一个字节由8位组成。在二进制记法中，它能表示的范围为从000000002到111111112；在十进制记法中，它能表示的范围为从010 to 25510。这两种记法都不适合描述位模式。二进制太冗长，在位模式和十进制之间来回转换十分麻烦。于是，我们用十六进制整数来写位模式。十六进制用数字0到9和字母和字符A到F来表示16个可能的值。Figure 2.2展示了这16个十六进制数字对应的二进制和十进制值。用十六进制表示，单个字节能表示的范围为从0016到FF16。

在C语言中，以0x或者0X开始的数字常量被解释为十六进制表示的数。字符A到F既可以写成大写，也可以写成小写。例如，我们可以把数FA1D37B16写成0xFA1D37B,或者 0xfa1d37b,  或者混合着大小写的 0xFa1D37b。在这本书中，我们将用C中记法来表示十六进制值。

在机器级程序中一个常见的任务是在位模式的二进制、十进制和十六进制表示之间转换。二进制和十六进制之间的转换是非常直接的，因为我们可以一次转换一个十六进制数字。每个数字的转换可以通过参考像Figure 2.2这样的图标来完成。在你的脑海中进行这个转换的一个简单的技巧是记住十六进制数字A，C和F的十进制值。十六进制数字B，D和E的十进制值可用它们相对A，C，F的值推导出来。

例如，假设有个数0x173A4C。你可以通过扩展每一个十六进制数字的方式把它转化为二进制格式，像下面这样：

转化后的二进制为000101110011101001001100。

反过来，给你一个二进制数1111001010110110110011，你可以通过把所有位分为四位一组的方式把它转化为十六进制。需要注意的是，如果位的数目不是四的整数倍，少于四位的那个组应该是最左边那个，然后用前导的0补齐这个组。然后，你把每一组都转化为对应的十六进制数字：

当一个值是2的幂的时候，也就是说，x = 2^n，n是一个非负数，我们可以通过记住x的二进制表示只是1后面跟着n个0，然后轻而易举地把它写作十六进制。因此，把n写作i + 4j，其中0 ≤ i ≤ 3，我们通过一个先导的十六进制数字1 (i = 0), 2 (i = 1), 4 (i = 2), or 8
(i = 3),跟着j个十六进制0来表示x。例如，x = 2048 = 2^11，n = 11= 3 + 4 . 2，得到十六进制表示0x800。

在十进制和十六进制之间转化需要用到乘法和除法。为了把十进制数x转化为一个十六进制，我们可以重复的用x除以16，得到商q和余数r，也就是说，x = q . 16 + r。我们可以用十六进制数字表示这个数，把它作为的到的权重最小的那个数字，然后在q上重复这个过程得到剩下的数字，例如，把十进制314156转化为十六进制：

314156 = 19634 . 16 + 12 (C)
19634 = 1227 . 16 + 2 (2)
1227 = 76 . 16 + 11 (B)
76 = 4 . 16 + 12 (C)
4 = 0 . 16 + 4 (4)

我们得到十六进制表示0x4CB2C。

反过来，反过来，把一个十六进制转化为十进制，我们可以把每一个十六进制数字乘以一个恰当的16的幂。例如，十六进制数0x7AF，它的十进制等于7 . 162 + 10 . 16 + 15 =
7 . 256 + 10 . 16 + 15 = 1792 + 160 + 15 = 1967。