碰撞检测之Box-Box检测
2D情况
首先回顾一下SAP
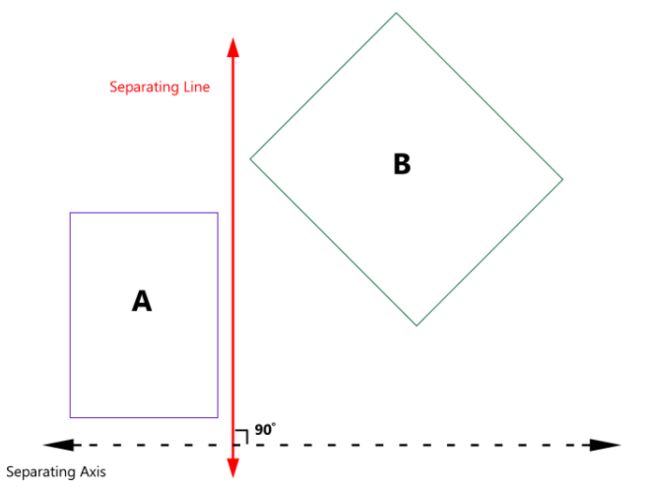
两个凸包多边形,当且仅当存在一条线,这两个多边形在这条线上的投影不相交,则这两个多边形也不相交.
这条线称为Separating Axis.垂直Separating Axis存在一条Separating Line将两个多边形分开。
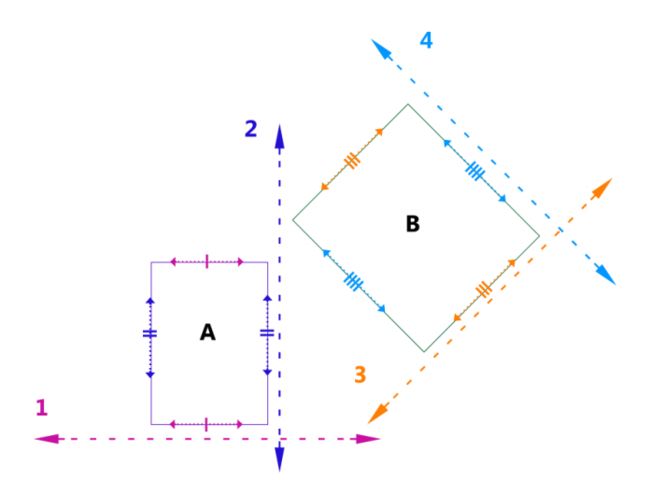
这里还有一个要确定的,就是如果两个矩形之间存在Separating Line,则一定存在一条和两个矩形中的一条边平行。每个矩形对边平行,则我们只需要检查四个方向是否存在Separating Line,如下图
找Separating Line 就是找Separating Axis, Separating Axis也只有四个方向,所以将矩形在四个轴上投影就可以了,如下图
下面来看具体的计算
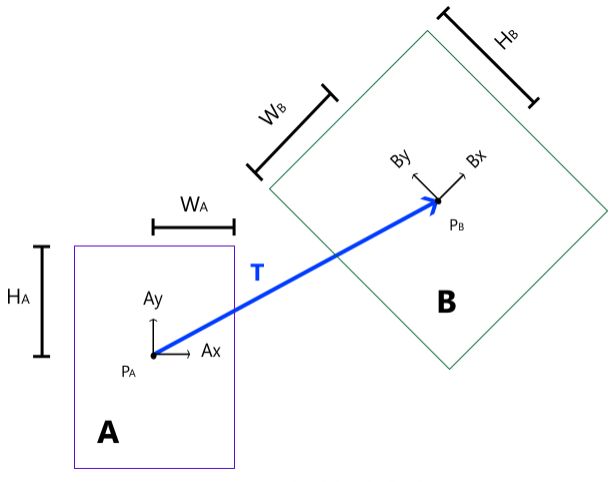
定义下面几个变量
PA = coordinate position of the center of rectangle A
Ax = unit vector representing the local x-axis of A
Ay = unit vector representing the local y-axis of A
WA = half width of A (corresponds with the local x-axis of A)
HA = half height of A (corresponds with the local y-axis of A)
PB = coordinate position of the center of rectangle B
Bx = unit vector representing the local x-axis of B
By = unit vector representing the local y-axis of B
WB = half width of B (corresponds with the local x-axis of B)
HB = half height of B (corresponds with the local y-axis of B)
T= PB - PA
轴L是Seprating Axis的条件是
|Proj ( T )| > 0.5 * |Proj ( RectangleA )| + 0.5 *|Proj ( RectangleB )|
Proj是投影计算, 展开
| T • L | > | ( WA*Ax ) • L | + | ( HA*Ay ) • L | + | ( WB*Bx ) • L | + |( HB*By ) • L |
L只有四种情况,AX, AY, BX, BY
CASE 1:
// L = Ax
| T • Ax | > | ( WA*Ax ) • Ax | + | ( HA*Ay ) • Ax | + | ( WB*Bx ) • Ax | + |( HB*By ) • Ax |
| T • Ax | > WA + 0 + | ( WB*Bx ) • Ax | + |( HB*By ) • Ax |
| T • Ax | > WA + | ( WB*Bx ) • Ax | + |( HB*By ) • Ax |
如果成立,存在Separating Axis平行Ax。
CASE 2:
// L = Ay
| T • Ay | > HA + | ( WB*Bx ) • Ay | + |( HB*By ) • Ay |
如果成立,存在Separating Axis平行Ay。
CASE 3:
// L = Bx
| T • Bx | > | ( WA* Ax ) • Bx | + | ( HA*Ay ) • Bx | + WB
如果成立,存在Separating Axis平行Bx。
CASE 4:
// L = By
| T • By | > | ( WA* Ax ) • By | + | ( HA*Ay ) • By | + HB
如果成立,存在Separating Axis平行By。
三维情况
在三维情况下的,之前的Separating Line就变成了Separating Plane,如下图
每个Box都有三组面,每组面都是平行的,Separating Plane都是平行其中的一个面。则两个box的SAT中可能的Separating Axis有六个
下图中Separating Plane就平行于右边Box的一个面
然而还有一种情况,如下
这种情况,两个Box并不相交,但是他们并没有发生碰撞,这种情况,Separating Plane的法线是两条红线的叉乘
所以在三维情况下Box和Box的碰撞检测需要判定的情况有6+9种
CASE 1:L = Ax CASE 2:L = Ay CASE 3:L = Az CASE 4:L = Bx CASE 5:L = By CASE 6:L = Bz
CASE 7:L = Ax Bx CASE 8:L = Ax By CASE 9:L = Ax Bz CASE 10:L = Ay Bx
CASE 11:L = Ay By CASE 12:L = Ay Bz CASE 13:L = Az Bx CASE 14:L = Az By CASE 15:L = Az Bz
判断条件还是
| T • L | > | ( WA*Ax ) • L | + | ( HA*Ay ) • L | + |( DA*Az ) • L |+ | ( WB*Bx ) • L | + |( HB*By ) • L | + |( DB*Bz ) • L |
一点优化,关于T • L
T • (Ax * Bx) =(T • Az)(Ay • Bx) - (T• Ay)(Az • Bx)
这里将有叉乘的地方进行了转化,要看证明的请看参考资料。
好,可以上代码了
public static bool IntersectBoxBox(Box box0, Box box1)
{
Vector3 v = box1.center - box0.center;
//Compute A's basis
Vector3 VAx = box0.rotation * new Vector3(1, 0, 0);
Vector3 VAy = box0.rotation * new Vector3(0, 1, 0);
Vector3 VAz = box0.rotation * new Vector3(0, 0, 1);
Vector3[] VA = new Vector3[3];
VA[0] = VAx;
VA[1] = VAy;
VA[2] = VAz;
//Compute B's basis
Vector3 VBx = box1.rotation * new Vector3(1, 0, 0);
Vector3 VBy = box1.rotation * new Vector3(0, 1, 0);
Vector3 VBz = box1.rotation * new Vector3(0, 0, 1);
Vector3[] VB = new Vector3[3];
VB[0] = VBx;
VB[1] = VBy;
VB[2] = VBz;
Vector3 T = new Vector3(Vector3.Dot(v, VAx), Vector3.Dot(v, VAy), Vector3.Dot(v, VAz));
float[,] R = new float[3, 3];
float[,] FR = new float[3, 3];
float ra, rb, t;
for (int i = 0; i < 3; i++)
{
for (int k = 0; k < 3; k++)
{
R[i, k] = Vector3.Dot(VA[i], VB[k]);
FR[i, k] = 1e-6f + Mathf.Abs(R[i, k]);
}
}
// A's basis vectors
for (int i = 0; i < 3; i++)
{
ra = box0.extents[i];
rb = box1.extents[0] * FR[i, 0] + box1.extents[1] * FR[i, 1] + box1.extents[2] * FR[i, 2];
t = Mathf.Abs(T[i]);
if (t > ra + rb) return false;
}
// B's basis vectors
for (int k = 0; k < 3; k++)
{
ra = box0.extents[0] * FR[0, k] + box0.extents[1] * FR[1, k] + box0.extents[2] * FR[2, k];
rb = box1.extents[k];
t = Mathf.Abs(T[0] * R[0, k] + T[1] * R[1, k] + T[2] * R[2, k]);
if (t > ra + rb) return false;
}
//9 cross products
//L = A0 x B0
ra = box0.extents[1] * FR[2, 0] + box0.extents[2] * FR[1, 0];
rb = box1.extents[1] * FR[0, 2] + box1.extents[2] * FR[0, 1];
t = Mathf.Abs(T[2] * R[1, 0] - T[1] * R[2, 0]);
if (t > ra + rb) return false;
//L = A0 x B1
ra = box0.extents[1] * FR[2, 1] + box0.extents[2] * FR[1, 1];
rb = box1.extents[0] * FR[0, 2] + box1.extents[2] * FR[0, 0];
t = Mathf.Abs(T[2] * R[1, 1] - T[1] * R[2, 1]);
if (t > ra + rb) return false;
//L = A0 x B2
ra = box0.extents[1] * FR[2, 2] + box0.extents[2] * FR[1, 2];
rb = box1.extents[0] * FR[0, 1] + box1.extents[1] * FR[0, 0];
t = Mathf.Abs(T[2] * R[1, 2] - T[1] * R[2, 2]);
if (t > ra + rb) return false;
//L = A1 x B0
ra = box0.extents[0] * FR[2, 0] + box0.extents[2] * FR[0, 0];
rb = box1.extents[1] * FR[1, 2] + box1.extents[2] * FR[1, 1];
t = Mathf.Abs(T[0] * R[2, 0] - T[2] * R[0, 0]);
if (t > ra + rb) return false;
//L = A1 x B1
ra = box0.extents[0] * FR[2, 1] + box0.extents[2] * FR[0, 1];
rb = box1.extents[0] * FR[1, 2] + box1.extents[2] * FR[1, 0];
t = Mathf.Abs(T[0] * R[2, 1] - T[2] * R[0, 1]);
if (t > ra + rb) return false;
//L = A1 x B2
ra = box0.extents[0] * FR[2, 2] + box0.extents[2] * FR[0, 2];
rb = box1.extents[0] * FR[1, 1] + box1.extents[1] * FR[1, 0];
t = Mathf.Abs(T[0] * R[2, 2] - T[2] * R[0, 2]);
if (t > ra + rb) return false;
//L = A2 x B0
ra = box0.extents[0] * FR[1, 0] + box0.extents[1] * FR[0, 0];
rb = box1.extents[1] * FR[2, 2] + box1.extents[2] * FR[2, 1];
t = Mathf.Abs(T[1] * R[0, 0] - T[0] * R[1, 0]);
if (t > ra + rb) return false;
//L = A2 x B1
ra = box0.extents[0] * FR[1, 1] + box0.extents[1] * FR[0, 1];
rb = box1.extents[0] * FR[2, 2] + box1.extents[2] * FR[2, 0];
t = Mathf.Abs(T[1] * R[0, 1] - T[0] * R[1, 1]);
if (t > ra + rb) return false;
//L = A2 x B2
ra = box0.extents[0] * FR[1, 2] + box0.extents[1] * FR[0, 2];
rb = box1.extents[0] * FR[2, 1] + box1.extents[1] * FR[2, 0];
t = Mathf.Abs(T[1] * R[0, 2] - T[0] * R[1, 2]);
if (t > ra + rb) return false;
return true;
}
测试代码
public class BoxBoxTester : MonoBehaviour {
public GameObject box;
public GameObject box1;
Box _box;
Box _box1;
// Use this for initialization
void Start()
{
_box = new Box();
_box1 = new Box();
}
// Update is called once per frame
void Update()
{
_box.center = box.transform.position;
_box.rotation = box.transform.rotation;
_box.extents = 0.5f * box.transform.localScale;
_box1.center = box1.transform.position;
_box1.rotation = box1.transform.rotation;
_box1.extents = 0.5f * box1.transform.localScale;
if (NIntersectTests.IntersectBoxBox(_box, _box1))
{
box.GetComponent<MeshRenderer>().materials[0].SetColor("_Color", new Color(1, 0, 0));
}
else
{
box.GetComponent<MeshRenderer>().materials[0].SetColor("_Color", new Color(1, 1, 1));
}
}
}
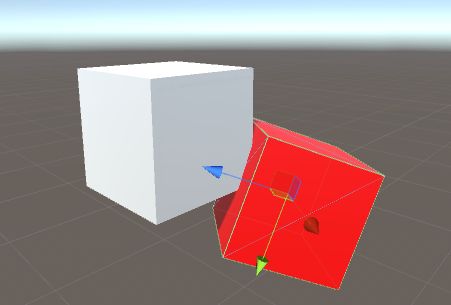
运行结果
参考
Separating Axis Theorem for Oriented Bounding Boxes