动态规划算法解LCS问题的JS实践
LCS (最长公共子序列)
定义:一个数列 S,如果分别是两个或多个已知数列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
如有两个字符串:1235和136,则:
1, 12, 123, 1235, 2, 23, ..., 1235是字符串1235的子序列
1, 3, 13, 36, ..., 136是136的子序列
13是1235和136的最长公共子序列
LCS问题即求两集合最长公共子序列的问题
理论基础
设有:
Xi=﹤x1,⋯,xi﹥即X序列的前i个字符 (1≤i≤m)(前缀)
Yj=﹤y1,⋯,yj﹥即Y序列的前j个字符 (1≤j≤n)(前缀)
注:X和Y是从1开始算起
假定Z=﹤z1,⋯,zk﹥∈LCS(X , Y)。
即Z为Xi和Yj的最长公共子序列
若zm=zn(最后一个字符相同),则:该字符必是x与y的任一最长公共子序列Z(设长度为k)的最后一个字符
若zm≠zn,则Zk要么属于ym-1,要么属于yn-1
设Xi和Yj最长公共子序列的长度为C[i,j],则有(公式1):
c[i, j] = 0 //when i = 0 or j = 0
C[i, j] = c[i - 1, j - 1] + 1; //when zm = zn
c[i, j] = max(c[i, j - 1], c[i - 1, j]) //when zm ≠ zn
那么,接下来的目标就是,想办法判断子序列的最后一个字符是只属于X序列还是只属于Y序列,还是属于X序列和Y序列。
而当c[i,j-1] > c[i-1,j]的时候,最长子序列的最后一个字符存在于xi中,反之,存在于yj中
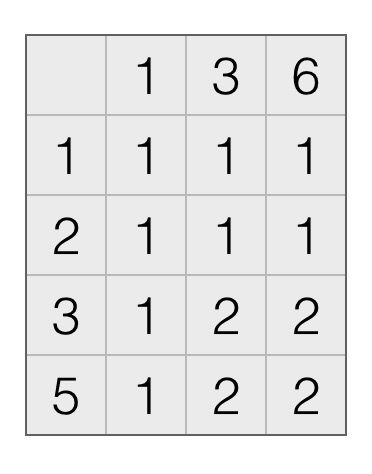
以序列 X:1235 和 Y:136 为例,根据公式1,可以得出以下表格(图1):
举例来说,当x为5,y为6时,序列1235和136的最长公共子序列长度为2;
当x为2,y为3时,序列12和13的最长公共子序列长度为1。
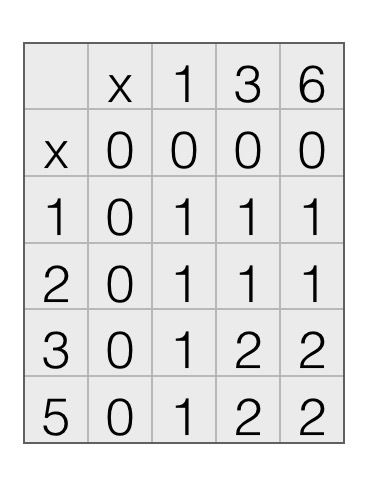
因为存在 c[i, j] = c[i - 1, j - 1] + 1 这样的运算,如果数组以0为开头,会出现下标为-1的情况,所以将表格改变为如下形式,x行和x列没有实际意义:
JavaScript代码以数组的形式生成以上表格的代码如下:
var arr = []; //array init
for (var i = 0; i < str1.length + 1; i++) {
arr[i] = []; for (var j = 0; j < str2.length + 1; j++) {
arr[i][j] = 0;
}
}
for (var i = 1; i < str1.length + 1; i++) {
for (var j = 1; j < str2.length + 1; j++) {
if (str1[i - 1] == str2[j - 1]) {
arr[i][j] = arr[i - 1][j - 1] + 1;
} else if (arr[i - 1][j] >= arr[i][j - 1]) {
arr[i][j] = arr[i - 1][j];
} else {
arr[i][j] = arr[i][j - 1];
}
}
}
接下来,根据这个表格去计算出最长公共子序列
首先以序列X的最后一个字符5和Y的最后一个字符6进行比较,
i为4,j为3,长度为c[4,3]=2,5≠6,又因为c[4,2]=c[3,3],再以c[4,2]开始进行比较
i为3,j为3,长度为c[4,2]=2,5≠3,又因为c[4,2]<c[3,2],再以c[3,2]开始进行比较
...
蓝色部分为比较时经过的路径,最后得出1,3最长公共子序列
JavaScript实现代码为:
function _lcs(str1, str2, i, j, arr, result) {
if (i == 0 || j == 0) {
return;
}
if (str1[i - 1] == str2[j - 1]) {
_lcs(str1, str2, i - 1, j - 1, arr, result);
result.push(str1[i - 1]);
} else if (arr[i][j - 1] >= arr[i - 1][j]) {
_lcs(str1, str2, i, j - 1, arr, result);
} else {
_lcs(str1, str2, i - 1, j, arr, result);
}
}
最后,完整的实验代码是:
function lcs(str1, str2) {
var arr = []; //array init
for (var i = 0; i < str1.length + 1; i++) {
arr[i] = [];
for (var j = 0; j < str2.length + 1; j++) {
arr[i][j] = 0;
}
}
for (var i = 1; i < str1.length + 1; i++) {
for (var j = 1; j < str2.length + 1; j++) {
if (str1[i - 1] == str2[j - 1]) {
arr[i][j] = arr[i - 1][j - 1] + 1;
} else if (arr[i - 1][j] >= arr[i][j - 1]) {
arr[i][j] = arr[i - 1][j];
} else {
arr[i][j] = arr[i][j - 1];
}
}
}
var result = [];
_lcs(str1, str2, str1.length, str2.length, arr, result);
console.log(result)
}
function _lcs(str1, str2, i, j, arr, result) {
if (i == 0 || j == 0) {
return;
}
if (str1[i - 1] == str2[j - 1]) {
_lcs(str1, str2, i - 1, j - 1, arr, result);
result.push(str1[i - 1]);
} else if (arr[i][j - 1] >= arr[i - 1][j]) {
_lcs(str1, str2, i, j - 1, arr, result);
} else {
_lcs(str1, str2, i - 1, j, arr, result);
}
}
测试:
var str1 = "asdfg29hj40kl"; var str2 = "qw29e4r0tyuiop"; lcs(str1, str2);
输出:
[ '2', '9', '4', '0' ]
以上。
个人博客原文链接:http://www.zcmyworld.com/singleArticle?articleId=334