Head First 栈与队列
目录
一、前言
二、LIFO——栈
1、栈的概述
2、栈的基本算法
三、栈的应用
1、进制转换
2、括号匹配问题
3、行编辑问题
4、表达式求值
四、FIFO——队列
1、队列的顺序存储
2、队列的链式存储
3、循环队列
***********************************************
--------------------------------------分割线-------------------------------------------
一、前言
本文是“Head First 数据结构”系列第二篇,主要记录栈和队列这一章的知识。栈和队列都是特殊的线性表,所以许多操作与线性表有一定的相似之处,甚至对于一些基本操作而言要比线性表简单。并且大多视频讲解时都会“轻实现,重实践”,所以本文以栈和队列的应用为主。本着上一篇博文中提到的将严版“初学者杀手”——伪代码进行实现的原则,本文将主要介绍该书中提到的、同时也是栈的最经典的几个应用。
--------------------------------------分割线-------------------------------------------
二、LIFO——栈
1、栈的概述
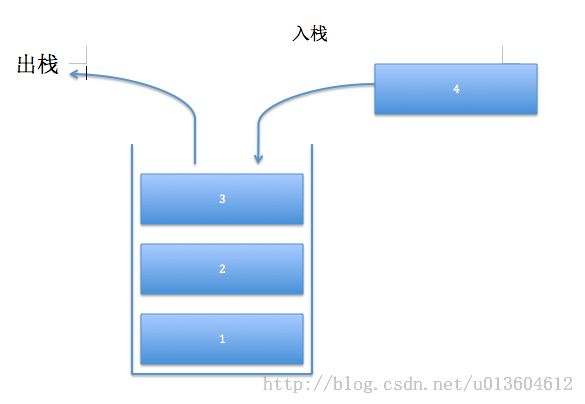
如前所述,栈是线性表的一种特殊情况,特殊就特殊在这个“LIFO”也就是“last - in - first - out(后进先出)”,可以说栈只有一个进出口,最先进来的元素被压入栈底,出元素的时候要从栈顶弹出。如图
正是因为这个特性,栈的应用非常广泛,接下来再稍稍讲过栈的一些基本操作之后我们就看一些经典应用。
2、栈的基本算法
首先我们需要看一下栈的表示。同样栈分为顺序存储和链式存储两种方式。
顺序存储时,一般为了操作方便,我们设立两个指针——栈顶指针和栈底指针来表示一个栈。另外,栈在用顺序存储方式时,由于栈的大小难以确定,最合适的方法就是动态分配内存空间的方法,即初始化时先分配一段长度的内存,然后在压栈时如果容量满了,就另外动态分配一段内存供栈使用。我们可以为其加一个变量stackSize来表示当前栈已分配的空间。即:
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define OVERFLOW -2
#define NULLSTACK -1
#define STACK_INIT_SIZE 80
#define INCREMENT_SIZE 10
#define MAXSIZE 200
typedef char ElemType;
typedef int Status;
typedef int BOOL;
typedef struct
{
ElemType *base; //栈底指针
ElemType *top; //栈顶指针
int stackSize; //栈容量
}SqStack;
这样,按照刚才所说的便能写出顺序栈的初始化方法:
1)栈的初始化
思路:分配一段内存空间,令栈顶和栈底指针同时指向这段空间代表栈为空。
代码:
Status InitSqStack(SqStack *S)
{
(*S).base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(SqStack));
if ((*S).base == NULL) {
return OVERFLOW;
}
(*S).top = (*S).base;
(*S).stackSize = STACK_INIT_SIZE;
return OK;
}
有了栈顶和栈底指针,许多操作在实现的时候就需要注意一下。这里我们规定栈底指针指向栈底的元素,栈顶指针指向栈顶元素的下一个位置,即“下一个插入时的位置”。因此栈的判空就是S.base == S.top ? YES : NO;这里着重讲一下压栈操作,因为这其中涉及到内存的重分配问题。
2)压栈:
思路:由于当前栈有可能已满,所以需要判断,如果是,则应该重新分配内存空间,定位栈底指针,然后通过地址偏移量重新定位出栈顶指针,再将栈容量增加。插入时要注意(*S).top指向的是“下一个插入的位置”。所以直接在(*S).top插入即可。
代码:
Status Push(SqStack *S, ElemType e)
{
if ((*S).top - (*S).base >= (*S).stackSize) { //如果当前栈满
(*S).base = (ElemType *)realloc(S, (*S).stackSize + INCREMENT_SIZE); //重新定位栈底指针
if ((*S).base == NULL) {
return OVERFLOW;
}
(*S).top = (*S).base + (*S).stackSize; //重新定位栈顶指针
(*S).stackSize += INCREMENT_SIZE; //栈容量增加
}
*((*S).top) = e; //栈顶元素为e
(*S).top++; //栈顶指针后移
return OK;
}
其他的操作都不是那么复杂,注意好栈顶指针的操作即可。这里就将这些代码附到附件上供参考。
而对于栈的链式存储则更为简单明了,毕竟栈本身就是特殊的线性表。则例仅给出数据结构定义,详细操作可以参考附件。
typedef struct StackNode
{
ElemType data;
struct StackNode *next;
}StackNode, *LinkStackPtr;
typedef struct LinkStack
{
LinkStackPtr top;
int count;
}LinkStack;
--------------------------------------分割线-------------------------------------------
三、栈的应用
1、数值转换
之前说过,很多情况下问题都符合栈的后进先出的特点,因此栈的应用很广泛。让我们从第一个例子开始看起吧。
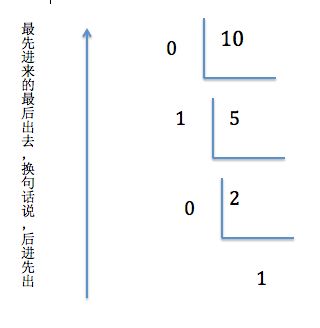
如上图,我们以前在做二进制的问题时就是这样做的(万恶的山东基本能力- -|)。通过上图可以看出,最先算出来的数是最后输出的,也就是“后算先输”,这就可以用栈来实现。
思路:用要转换的数number去除以转换的进制to,记录结果和余数,余数压栈,结果继续除,直到结果为0.然后将栈输出即可。
代码:
/**
* 栈的应用
* 应用一:数制转换
* @prama S 栈数据结构指针
* @prama number 要转换的十进制数
* @prama to 转换成的进制
*/
void Conversion(SqStack *S, int number, int to)
{
InitSqStack(S);
while (number) {
Push(S, number % to);
number /= to;
}
int e;
while (!IsStackEmpty(*S)) {
Pop(S, &e);
printf("%d", e);
}
printf("\n");
}
数值转换应该算是栈最简单的一个应用了。
2、括号匹配问题
第一次见这个问题是在学c语言的时候看到acm题,当时被虐惨了。。
所谓括号匹配,就是以任意顺序输入一组括号,包括"("、"["、"{"、")"、"]"、"}"六种,判断是否能匹配。例如"{{}}[]([])"就是匹配的,而"{[}]"就是不匹配的.
思路:从例子中可以看出,如果输入的括号是左括号,则先让他们等着,当出现右括号时,让之前最后输入的那个左括号出来与之匹配,如果匹配,则消去这一对,否则返回NO,如果输入右括号时没有找到左括号,则返回NO,如果输入完后还有没有匹配的左括号,则返回NO。
从上述描述中可以找出“最后输入的那个左括号先出来”这样的意思。因此,该问题可以用栈来实现。
代码:
/**
* 栈的应用
* 应用二:括号匹配
* @prama S 栈数据结构指针
* @prama ch 包括所有括号的字符数组
* @retun BOOL TRUE(1)代表匹配,FALSE(0)代表不匹配
*/
BOOL Check(SqStack *S, char ch[])
{
InitSqStack(S);
char e;
int i = 0;
while (ch[i]) {
if (ch[i] == '(' || ch[i] == '[' || ch[i] == '{') {
Push(S, ch[i]);
i++;
}
else if (ch[i] == ')') {
if (IsStackEmpty(*S)) {
return FALSE;
}
Pop(S, &e);
if (e != '(') {
return FALSE;
}
i++;
}
else if (ch[i] == ']') {
if (IsStackEmpty(*S)) {
return FALSE;
}
Pop(S, &e);
if (e != '[') {
return FALSE;
}
i++;
}
else if (ch[i] == '}') {
if (IsStackEmpty(*S)) {
return FALSE;
}
Pop(S, &e);
if (e != '{') {
return FALSE;
}
i++;
}
}
if (!IsStackEmpty(*S)) {
return FALSE;
}
else {
return TRUE;
}
}
3、行编辑问题
当用户在输入时总会遇到输入错误的情况,“电脑”给了我们两种方法解决这一问题,一个是delete删除一位,一个是command+delete删除一行。现在我们来实现一下这一个功能。
思路:用一个字符数组接收用户输入的字符串,然后规定‘#’代表删除一位,‘@’代表删除一行。根据经验,删除一位就是删除“最后输入的那一位”,而删除一行则只需清空输入即可。
代码:
/**
* 栈的应用
* 应用三:行编辑问题
* @prama S 栈数据结构指针
* @prama ch 包括所有括号的字符数组
* @retun BOOL TRUE(1)代表匹配,FALSE(0)代表不匹配
*/
void EditLine(SqStack *S)
{
char ch, e;
InitSqStack(S);
ch = getchar();
while (ch != EOF) {
while (ch != EOF && ch != '\n') {
switch (ch) {
case '#':
Pop(S, &e);
break;
case '@':
ClearStack(S);
break;
default:
Push(S, ch);
break;
}
ch = getchar();
}
PrintStackReverse(*S);
ClearStack(S);
if (ch != EOF) {
ch = getchar();
}
}
DestoryStack(S);
}
4、表达式求值
大家在学习c语言时曾经写过最简单的“计算器”吧,也就是只能对两个操作数做一次运算的程序。不过我们平时用的计算器是输入一段式子就能给出正确的结果。所谓正确的结果就是指按照正确的优先级和结合性进行计算。这个要求如果不用栈可能就不大可能了。
为什么这个程序也要用栈呢?留下这个问题,我们先来看看表达式。
给出一个式子:4 + 2 * 3 - 10 / 5,大家马上就能认出来并口算出结果。
如果这样写呢:4 2 3 * 10 5 / - +,估计如果不是事先听说,连认都认不出这是个可计算的表达式吧。其实这就是所谓的“后缀表达式”,也就是操作符在两个操作数后面。前面分别是第一操作数和第二操作数,例如:3 4 -就是3 - 4。
为什么要介绍后缀表达式?因为对于表达式求值,用后缀表达式可以非常方便地得到结果,无需再考虑运算符的优先级。当然了,这并不是说只有这种方法。现在很多书都是介绍的后缀表达式法,但前缀表达式法和我们最熟悉的中缀表达式法都是没问题的。那现在我们就来看一下后缀表达式的实现思路。
思路:
首先,中缀表达式转后缀表达式。
对于四则表达式,求值的规则为:①先乘除后加减、②从左到右、③有括号先计算括号内。根据这三条,我们把中缀表达式转换成后缀表达式
上述①③实质上都是在说运算符优先级的事,在转换时,我们从左到右扫描表达式,如果遇到+ 、-运算则不急于计算,例如:3 + 5 * 4如果先计算了3 + 5就错了。也就是说,遇到一个运算符先不急于算,后面可能有比它优先级高的。但是如果后面一个运算符优先级不如它高,那么就代表前面的已经可以计算了,这里输出即可。为此我们可以设立两个表,一个是操作符栈,因为这里很明显的后进去的运算符先计算(输出)。另一个用来存储后缀表达式,当扫描到数字时直接进来,而遇到运算符时先进栈,经过刚才的过程后再将合适的运算符拿到第二个表中。最后,第二个表中的结果就是后缀表达式,到时候“按序”计算即可。不过第二个表是什么呢?它的特征是先进来的运算时先出去,也就是一会要说的队列。
接下来我们就来看一下怎么计算后缀表达式,其实计算起来就简单了。我们可以设立一个空栈,从左到右扫描后缀表达式,若是操作数则进栈,若是运算符,则从栈中弹出两个数运算,然后重新压到栈中,最后留在栈中的数就是结果了。
具体要求可以见数据结构严蔚敏版,实现由于较长,在这里就不给出了,可以参考附件“Head First 栈和队列”
--------------------------------------分割线-------------------------------------------
四、FIFO——队列
1、队列的顺序存储
正如刚才表达式求值应用中提到的,队列是一种与栈相反的结构,就像我们排队一样,先进先出。队列也是线性表的一种,所以简单的队列实现起来并不难。所以接下来就直接给出了。
队列的定义:
typedef struct {
ElemType data[MAXSIZE];
int front; //头指针
int rear; //尾指针
}SqQueue;同样我们为队列设置头指针和尾指针来简化后序操作。
这里就不给出普通的顺序存储的实现了,因为这是我们绝对不会用到的,因为这样会造成十分严重的空间浪费。详情到循环队列在讲述。
2、队列的链式存储
数据结构定义:
typedef struct QueueNode
{
ElemType data;
struct QueueNode *next;
}QueueNode, *QueuePtr;
typedef struct {
QueuePtr front, rear; //队头、队尾指针
}LinkQueue;注意:这里的队头指针并不指向实际数据,仅表示一个队列的开始,和线性表的头指针一样。而队列的判空条件就是Q.front == Q.rear。
这里说一下队列的出对操作:
思路:找到第一个元素,用一个元素记录其值,然后将其删除。需要注意的是,如果这是队列的最后一个元素,那么需要更改Q.rear使之等于Q.front。
代码:
Status DeQueue(LinkQueue *Q, ElemType *e)
{
if (Q->front == Q->rear) {
return ERROR;
}
QueuePtr p;
p = Q->front->next;
*e = p->data;
Q->front->next = p->next;
if (Q->rear == p) {
Q->rear = Q->front;
}
free(p);
return OK;
}
3、循环队列
循环队列其实才是真正的队列的顺序表示。如之前所说,如果不用循环队列,假设队列出队了若干元素,如果前面的空间不加以利用,则会浪费大量的空间。如图:

所以在队列尾部“满了”以后我们要重新利用前面已经不用了得空间。
还是利用之前的数据结构定义,我们来看看循环队列的基本操作
1)判空、判满与长度
思路:判空依旧是一样的,循环队列的头尾指针都是要动的,不过只要这两个指针相等,就说明队列是空的。
而判满则需要一定的计算了,其实找找规律也不难发现,当Q.rear + 1对队列的最大长度MAXSIZE取余后如果等于Q.front则说明队列是满地。
计算长度的时候,如果Q.rear在Q.front之后,则很明显是Q.rear - Q.front,而由于循环队列的性质,Q.rear很有可能在Q.front之前,此时可以看出,上述结果对MAXSIZE取余后就是队列的长度。
代码:
int QueueLength(SqQueue Q)
{
return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}
BOOL IsQueueFull(SqQueue Q)
{
return (Q.rear + 1) % MAXSIZE == Q.front ? TRUE : FALSE;
}
BOOL IsQueueEmpty(SqQueue Q)
{
return Q.front == Q.rear ? TRUE : FALSE;
}
2)入队与出队
思路:入队唯一要注意的地方就是Q.rear在往后移的时候有可能因尾部满了而回到头部,所以将Q.rear += 1改为 Q.rear = (Q.rear + 1) % MAXSIZE即可。
出队时可以通过移动头指针来实现,同样,要注意Q.rear移到最后再重新回到起点时的情形,和上面入队一样。
代码:
Status EnQueue(SqQueue *Q, ElemType e)
{
if (IsQueueFull(*Q)) {
return ERROR;
}
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % MAXSIZE;
return OK;
}
Status DeQueue(SqQueue *Q, ElemType *e)
{
if (IsQueueEmpty(*Q)) {
return ERROR;
}
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % MAXSIZE;
return OK;
}
--------------------------------------分割线-------------------------------------------
到此,Head First 数据结构系列第二篇也就完结了,这两篇算是假期自学的学习笔记吧,希望对大家有所帮助。从下一章串开始我打算等我们课程开了以后我再用博文当学习笔记来写。明天转战iOS
附:
Head First 栈和队列