棋盘上礼物价值最大化问题-微策略2011校园招聘笔试题
题目:8*8的棋盘上面放着64个不同价值的礼物,每个小的棋盘上面放置一个礼物(礼物的价值大于0),一个人初始位置在棋盘的左上角,每次他只能向下或向右移动一步,并拿走对应棋盘上的礼物,结束位置在棋盘的右下角,请设计一个算法使其能够获得最大价值的礼物。
解题:
这是一个经典的动态规划问题。
首先是动态规划遵守的4个步骤:
1 描述最优解的结构
2 递归定义最优解的值
3 按自底向上的方式计算最优解的值
4 由计算出的结果构造一个最优解
(本段来自《算法导论》第192页)
根据上面的理论结合本题我们可以得出如下的步骤:
1 最优解的结构:要当前格的价值最大化,则需要判断当前格的上面一格加上当前格的礼物价值和左边一格的加上当前格的礼物价值,取最大的即可。
2 递归定义:f(i,j)=max(f(i-1,j),f(i,j-1))+a[i][j]。如果是第一行则:f(0,j)=f(0,j-1)+a[0][j]。如果是第一列则:f(i,0)=f(i-1,0)+a[i][0]。
3 自底向上求解:即从第一行第一列开始循环求解即可。
4 根据循环的结果构造最优解。
解题:
这是一个经典的动态规划问题。
首先是动态规划遵守的4个步骤:
1 描述最优解的结构
2 递归定义最优解的值
3 按自底向上的方式计算最优解的值
4 由计算出的结果构造一个最优解
(本段来自《算法导论》第192页)
根据上面的理论结合本题我们可以得出如下的步骤:
1 最优解的结构:要当前格的价值最大化,则需要判断当前格的上面一格加上当前格的礼物价值和左边一格的加上当前格的礼物价值,取最大的即可。
2 递归定义:f(i,j)=max(f(i-1,j),f(i,j-1))+a[i][j]。如果是第一行则:f(0,j)=f(0,j-1)+a[0][j]。如果是第一列则:f(i,0)=f(i-1,0)+a[i][0]。
3 自底向上求解:即从第一行第一列开始循环求解即可。
4 根据循环的结果构造最优解。
算法如下:
#include<iostream.h>
//内联函数 用来比较大小
inline int max(int a,int b)
{
return a>b?a:b;
}
int maxvalue(int a[6][6])
{
int f[6][6]={0};
//循环
for(int i=0;i<6;i++)
{
for(int j=0;j<6;j++)
{
//如果是第一行第一列
if(0==i && 0==j)
{
f[i][j]=a[0][0];
}
//如果是第一行
else if(0==i)
{
f[i][j]=f[i][j-1]+a[i][j];
}
//如果是第一列
else if(0==j)
{
f[i][j]=f[i-1][j]+a[i][j];
}
//其他列处理
else
{
f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
}
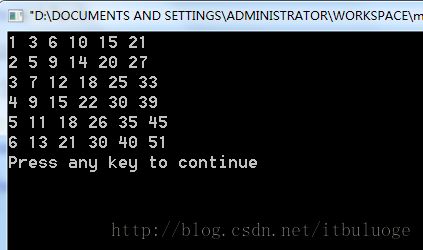
cout<<f[i][j]<<" ";//打印最优值
}
cout<<endl;//打印最优值
}
return f[5][5];
}
int main()
{
//测试数据
int a[6][6]=
{
{1,2,3,4,5,6},
{1,2,3,4,5,6},
{1,2,3,4,5,6},
{1,2,3,4,5,6},
{1,2,3,4,5,6},
{1,2,3,4,5,6}
};
maxvalue(a);
return 0;
}

文章来自IT部落格