Aztec 钻石问题（一）：蜘蛛移动

这篇文章里要介绍的是非常精彩的 Aztec 钻石问题。我觉得这是一个可以进入 "数学天书" 的问题，它的表述简单而初等，但是却与计数组合学中许多最深刻美妙的问题有着千丝万缕的联系，当然它还有一个令人拍案叫绝的解法。所有这些不能不让我把它写出来和大家分享。

问题表述 

 

什么是 Aztec 钻石模型呢？很简单：依次把 $2,4,\cdots,2n$ 个方格摞在一起，然后关于 $x$ 轴对称地反射过去，得到的图形就叫 $n$ 阶 Aztec 钻石图 $AZ_n$，Aztec 钻石图的一个多米诺铺砌是指用 $1\times2$ 的骨牌不重复不遗漏地恰好盖住整个图形：（例子中 $n=30$）

 

我们的问题是： $AZ_n$ 一共有多少种不同的多米诺铺砌？

多米诺铺砌本质上属于完美匹配问题的范畴：考虑一张新图 $G_n$，$AZ_n$ 的每个方格看作是 $G_n$ 中的顶点，$G_n$ 中的两个顶点相邻当且仅当它们对应的方格在 $AZ_n$ 中有公共的边。

 

 

现在问题转化为求 $G_n$ 的完美匹配的个数，基本的想法是权函数。

设 $G$ 是一个简单平面图，$G$ 的每条边 $e$ 有一个权值 $w(e)$，$w(e)$ 通常是一个变量，比如 $x,y,z,w$。对 $G$ 的每一个完美匹配 $M$，定义 $M$ 的权值 $w(M)$ 为 $M$ 中所有边的权值的乘积：\[w(M)=\prod_{e\in M}w(e),\]

然后定义 $G$ 的权函数 $M(G)$ 为 $G$ 的所有完美匹配的权值的和：

\[ M(G)=\sum_{M}w(M).\]

如果 $G$ 的每条边的权值都是 1，那么 $M(G)$ 就是 $G$ 的完美匹配的个数。但是一般情况下，边的权值 $w(e)$ 是一个未定元，所以 $M(G)$ 是一个包含未定元的多元函数。但是只要求出了权函数 $M(G)$ 的表达式，那么只要把其中所有变元都赋值为 1，就得到了 $G$ 的完美匹配的个数。

能求出权函数来当然是一件好事，因为权函数里面包含了图的非常多的信息，可以帮助我们计算出许多其它感兴趣的量来。比如说指定一条边 $e$，问 $G$ 有多少个匹配不包含 $e$？为此只要把边 $e$ 的权值设置为 0，其它的边权值保持为 1，代入权函数中即可。

看起来求出图的权函数是一个比直接计算其完美匹配的个数更复杂的问题，那为什么我们要舍近求远呢？权函数方法的奥秘在哪里呢？

这就是关键所在：对于一个复杂的图，我们想通过一些 "手术" 或者说 "变换" 把它变成简单一些的图，比如删去一些顶点和边，或者把其中的一部分用一个新图去替换。当然这些变换通常会改变图的完美匹配的个数，但是权函数却在变换前后保持某种不变性或者说相似性，这样我们就可以找到权函数所满足的递推关系进而把它求出来。

Aztec 钻石模型是由 N. Elkies，G. Kuperberg，M. Larsen 和 J. Propp 在 1992 年的论文中提出来的，这是一篇很精彩的文章，但是也很难读懂（需要对代数组合学有比较深的了解）。在那篇文章中他们一共给了 4 种解法，可以说都非常的 "高深" 。时至今日有人统计 Aztec 钻石模型已经有不下一打的解法，然而最精彩的解法却毫无疑问是我们将要介绍的名为 "蜘蛛移动" 的方法。

我们需要两个简单但是不平凡的引理：

引理之一：顶点分裂

 

 

如图所示：设顶点 $v\in G$ 的邻居 $N(v)$ 可以分成两个不相交的集合 $N(v)=H\cup K$，这里 $H$ 和 $K$ 中允许有一个是空集，我们对图 $G$ 作一个简单的变换：从 $v$ 中分裂出两个新的顶点 $v',v''$，用 $v'$ "代替" $v$ 去和 $H$ 中的顶点相连，用 $v''$ "代替" $v$ 去和 $K$ 中的顶点相连，$v$ 与 $v',v''$ 之间的边权值定义为 1，则得到的新图 $G'$ 与原图有同样的权函数：$M(G)=M(G')$。

证明是非常简单的，读者可以自己尝试完成。

在西游记里面，孙悟空有一项绝技，拔出一把毫毛，吹一口气，喊一声变，这些毫毛就变作许多小孙悟空，然后乒乒乓乓打妖怪，这就是孙悟空的分身术。我们这里的想法也是让 $v$ 当一回孙悟空，让 $v',v''$ 这两个分身替它去连接 $H,K$，而它只要连接 $v',v''$ 就行。

顶点分裂引理通常属于预处理的步骤，对图的影响本质上不大。最核心的部分是我们要讲的第二个引理：蜘蛛移动。

 

引理之二：蜘蛛移动

假设图 $G$ 的某个局部如下图所示：

 

 

这里位于中心处的胞腔的四条边的权值分别为 $x,y,z,w$，胞腔与周围四个顶点 $A,B,C,D$ 相连的四条边的权值都是 1。

现在我们删去中心的胞腔，把 $A,B,C,D$ 连接为一个新的胞腔，并且规定边的权值为（记 $\Delta=xw+yz$）

\[w'=\frac{x}{\Delta},\quad z'=\frac{y}{\Delta},\quad x'=\frac{w}{\Delta},\quad y'=\frac{z}{\Delta}.\]

 

 

则得到的新图 $G'$ 与原图 $G$ 的权函数的关系为

\[M(G)=\Delta M(G').\]

证明：设 $S=\{A,B,C,D\}$，根据 $S$ 在 $G$ 中匹配的方式，可以把 $G$ 的所有完美匹配分成三大类：

I. $S$ 中的四个顶点与胞腔的四个顶点一一匹配：

II. $S$ 中的四个顶点都和外部的顶点匹配：

III. $S$ 中有两个顶点和胞腔中的顶点匹配，另外两个与外部的顶点匹配：

 

对 I 类的一个匹配 $M$，设 $M$ 中其余部分的边的因子乘积是 $Q$，则由于 $M$ 在内部的四条边权值是 1，因此 $\pi(M)=Q$。将内部的胞腔删除以后，我们有两种方式可以定义 $A,B,C,D$ 的匹配，即 $\{AB,CD\}$ 或者 $\{AD,BC\}$。前者的权值是 $y'z'Q$，后者权值是 $x'w'Q$，和为 $(x'w'+y'z')=Q/\Delta$。

 

 

总之对 I 类的每一个匹配，我们可以把它变成 $G'$ 中的两个匹配，变换之后的匹配权值之和是原来的 $1/\Delta$。

 

对 II 类中的匹配，由于胞腔的四个顶点是自己两两配对，这有两种可能的方式，它们的权分别是 $xwQ$ 和 $yzQ$，其中 $Q$ 仍然是匹配在其余部分的权的积。但是删掉胞腔以后这两种可能变成了一种，权值是 $Q$。

 

 

 

总之 II 类的匹配可以两两配对合并为 $G'$ 中的一个匹配，变换后的权值也是原来的 $1/\Delta$。

 

对 III 类中的一个匹配 $M$， 不妨设 $S$ 中的顶点 $\{B,C\}$ 与胞腔中的顶点匹配（其余三种可能的情形是 $\{A,B\}$，$\{C,D\}$，$\{A,D\}$，分析是类似的，而 $\{A,C\}$ 和 $\{B,D\}$ 是不可能出现的情形）。于是 $M$ 的权值为 $wQ$，而删去胞腔以后在不影响外部匹配的情况下只有一种方式定义为 $G'$ 中的匹配，权值为 $w'Q$，所以变换后的权值仍然是原来的 $\frac{x'Q}{wQ}=\frac{1}{\Delta}$。

 

 

综合上述三种情形我们就得到了 $M(G)=\Delta M(G')$。

 

最后一击

 

 

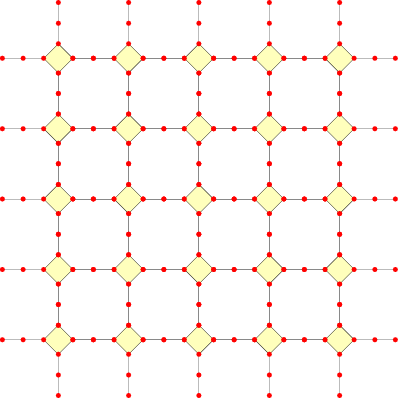
我们来给出 Aztec 钻石问题的解法：设 $G_n$ 的权函数为 $w(G_n)$，把它斜 45 度角放置，这样很清楚地显示了 $n^2$ 个胞腔，每个胞腔的边的权值和上面一样，顺时针方向为 $w,x,z,y$。

 

 

首先在 $n^2$ 个胞腔处反复地使用顶点分裂，我们得到下面这张图，新增加的边的权值都是 1：

 

 

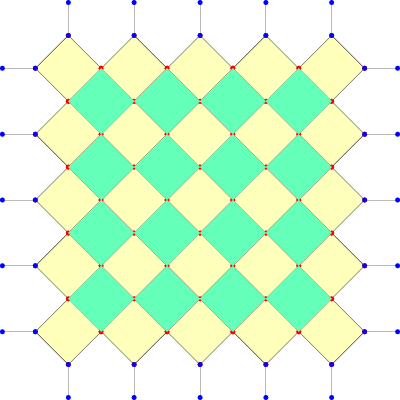
然后对第二张图在各个胞腔处使用 $n^2$ 次蜘蛛移动，得到第三张图：

 

 

第一张图和第二张图的权函数是一样的，都是 $w(G_n)$；经过 $n^2$ 次蜘蛛移动得到的第三张图的权函数为 $\frac{w(G_n)}{\Delta^{n^2}}$。

我们再换另一个角度来计算第三张图的权函数。这也是整个证明峰回路转，柳暗花明之处！注意第三张图的匹配在边界上是限制死的，真正自由的部分是内部的一个低一阶的图 $G_{n-1}$，所以可以剥去外面的这层环形回路！

 

 

而且这个子图的边的权值的标记规则是 $x/\Delta,y/\Delta,z/\Delta,w/\Delta$，因此这个子图的权函数为 $\frac{w(G_{n-1})}{\Delta^{n(n-1)}}$（因为 $G_{n-1}$ 的每个匹配包含 $n(n-1)$ 条边，是 $G_{n-1}$ 的顶点个数的一半）。从而我们用两种方法得到了第三张图的权函数，即\[\frac{w(G_n)}{\Delta^{n^2}}=\frac{w(G_{n-1})}{\Delta^{n(n-1)}},\]

也就是\[ w(G_n)=\Delta^nw(G_{n-1}),\]

注意 $n=1$ 时 $w(G_1)=\Delta$，从而 $w(G_n)=\Delta^{\frac{n(n+1)}{2}}$。特别令 $w=x=y=z=1$ 我们就得到 $n$ 阶 Aztec 钻石图 $AD_n$ 的所有多米诺骨牌覆盖的个数为 $2^{\frac{n(n+1)}{2}}$。

怎么样？整个过程是不是非常的精彩呢？蜘蛛移动很类似于电网络里面的 $Y-\Delta$ 变换，类似的图变换技巧在精确可解格点模型中是很常用的。

参考文献

1. Altenating sign matrices and domino tilings, Elkies, Kuperberg. 1991.

2. Generalized Domino-Shuffling, James Propp, 2000.

3. Random domino tilings and the arctic circle theorem, Jockush, Propp