复变函数可视化：区域着色法

区域着色法是复变函数可视化中比较常用的方法：对复平面上的点 $z$ 以及复变函数 $f(z)$，用 $f(z)$ 的值来规定 $z$ 点处的 HSV 颜色空间的值，然后再转换到 RGB 颜色空间。之所以先映射到 HSV 空间是因为 HSV 空间是直接面对人的视觉的，而 RGB 空间是面对机器硬件的。

 

这里怎样通过 $f(z)$ 的值规定 HSV 颜色是可以自由发挥的，不同的方法会得出不同的染色效果（但是不会改变图像的形状）。通常是根据 $f(z)$ 的模长和幅角来确定颜色。

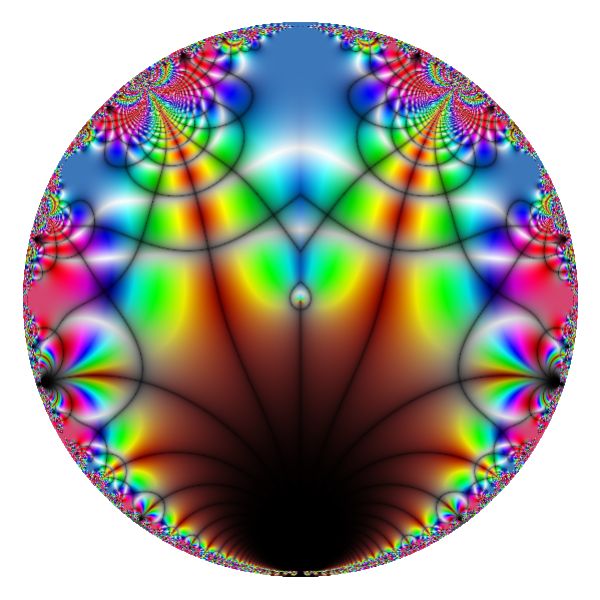
下图是 Rogers - Ramanujan 连分式的图像，我在程序的注释中写了简介。

 

 

程序中使用了 $\sin,\cos$ 等函数帮助起到平滑的效果。

 

# coding = utf-8

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import hsv_to_rgb
import time

"""
Rogers-Ramanujan 连分式是一个定义在复平面上单位圆盘 D(0,1) = {q: |q|<1} 上的复函数, 定义如下:

                                      1
            R(q) = q^{1/5} *  --------------------
                                         q
                               1 + --------------
                                           q^2
                                    1 +  ----------
                                               q^3
                                          1 + --------
                                               1 + ...

它可以用两列关于 q 的多项式来逼近:
设 {a_n(q)}, {b_n(q)} 是两个多项式序列, 满足递推关系
(1). a_0 = 1, a_1 = 1, b_0 = 1, b_1 = 1+q
(2). a_n = a_{n-1} + q^n * a_{n-2}
(3). b_n = b_{n-1} + q^n * b_{n-2}
即 {a_n} 和 {b_n} 的递推关系是一样的, 仅仅初始值不同.

则函数列 {f_n: f_n= a_n / b_n} 在 D 内收敛到 q^{-1/5} * R(q).

我们的目的就是在单位圆 D 内采集一些点 q, 选择一个 n (通常 n > 300), 
计算 f_n 在这些 q 处的值 f_n(q), 并把 q^{1/5} * f_n(q) 作为 R(q) 的近似值. 
根据这些 R(q) 的值规定 q 点的颜色, 当采集的点足够密集, 就显示出了 R(q) 的图像. 
"""


def Convergent(q,n):
    """
    计算 f_n(q). 这里 q 表示一个网格, 用多维数组同时计算 f_n(q) 的值, 
    返回的也是一个网格.
    """
    A = np.ones((q.shape)+(7,),dtype = 'complex')
    # A 的每个元素是一个长度为 7 的数组, 值为 a_{n-2}, a_{n-1}, a_n, b_{n-2}, b_{n-1}, b_n, temp.
    #初始时的值为 a_0, a_1, a_2, b_0, b_1, b_2, 1.
    B = A[...,3:6]
    temp = A[...,6]

    A[...,2] += q**2
    B[...,1] += q
    B[...,2] += q + q**2

    with np.errstate(over='ignore', divide='ignore', invalid='ignore'):
        for k in range(3,n+1):
            start = time.time()
            temp = A[...,2] + q**k * A[...,1]
            A[...,0], A[...,1], A[...,2] = A[...,1], A[...,2], temp
            temp = B[...,2] + q**k * B[...,1]
            B[...,0], B[...,1], B[...,2] = B[...,1], B[...,2], temp
            end = time.time()
            print ('compute %3d-th appoximation in %2f seconds' % (k, end-start))
        return A[...,2] / B[...,2]


def DomainColoring(f,re=(-1.5,1.5), im = (-1,5,1.5), N=400):
    x,y = np.ogrid[re[0]:re[1]:N*1j,im[0]:im[1]:N*1j]
    z = x + y*1j
    w = f(z)
    theta, r = np.angle(w), np.absolute(w)

    # 根据 w 的模长和幅角来规定 HSV 颜色空间的值.
    # 这里使用sin,cos函数是为了起到平滑的效果.
    with np.errstate(invalid='ignore'):
        H = np.absolute(np.sin(theta))   
        S = np.absolute(np.sin(2*np.pi*r))
        V = np.absolute(np.sin(2*np.pi*w.imag) * np.sin(2*np.pi*w.real)) ** 0.25    #取 0.25 幂是为了提高亮度 

    #对于不收敛的点, 统一染成白色, 即 HSV(0,0,1). 
    inf = np.where(np.isinf(w))
    nan = np.where(np.isnan(w))
    H[nan] = 0
    H[inf] = 0
    S[inf] = 0
    S[nan] = 0   
    V[inf] = 1
    V[nan] = 1
        
    HSV = np.dstack((H,S,V))
    return hsv_to_rgb(HSV)


img = DomainColoring(lambda q: q**(0.2)*Convergent(q,400),re=(-1.1,1.1),im=(-1.1,1.1),N=600)

fig = plt.figure(figsize=(6,6),dpi=100)
ax = fig.add_axes([0,0,1,1],aspect=1)
ax.axis('off')
plt.imshow(img)
plt.savefig('Rogers_Ramanujan_ContinuedFraction.png')

Rogers-Ramanujan 连分式

 

还有一种方法则是先把 $f(z)$ 的值用球极投影映射到 Riemann 球面上，根据得到的三个坐标 $(x,y,z)\in[-1,1]^3$ 来规定 HSV 颜色值。

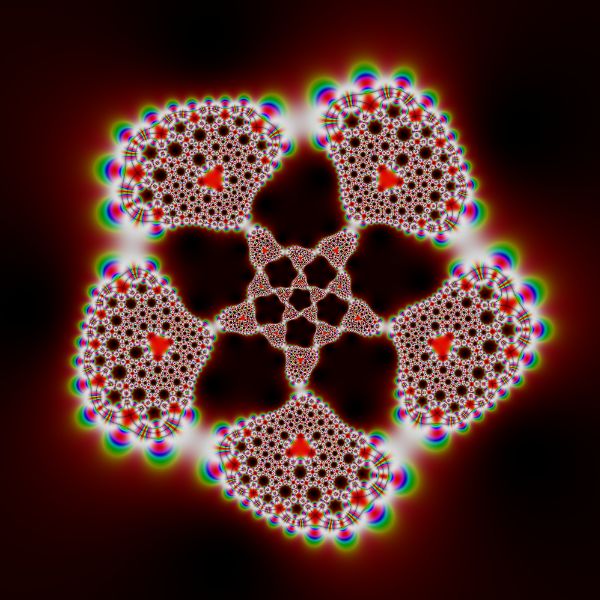
下图是 Klein $j-$ 函数的效果：

 

 

 

这里的 Klein $j-$ 函数是对称群 $A_5$ 下不变的，60 对 1 的映射，其图像非常对称。如果再和自身复合一次的话，同一个 $f(z)$ 值又会分出 60 个不同的原像来，就会出现上面类似 “分形” 的图案。中间我还复合了一个分式线性变换来扭曲图形。

 

#coding=utf-8

import numpy as np
import matplotlib.pyplot as plt
from numpy import sqrt, sin, cos, pi
from matplotlib.colors import hsv_to_rgb

def Icosahedron(z):
    return 1728*(z*(z**10+11*z**5-1))**5 / (-(z**20+1)+228*(z**15-z**5)-494*z**10)**3

def RiemannSphere(z):
    #将复平面上的点映射到Riemann球面上
    t = 1 + z.real**2 + z.imag**2
    return 2*z.real/t, 2*z.imag/t,2/t-1


def Mobius(z):
    return (z-20)/(3*z+1j)


x,y = np.ogrid[-6:6:1000j,-6:6:1000j]
z = x + y*1j

z = Icosahedron(z)
z = Mobius(z)
z = Icosahedron(z)
w = np.array(RiemannSphere(z))

H = sin(w[0,...]*pi)**2
S = cos(w[1,...]*pi)**2
V = abs(sin(w[2,...]*pi) * cos(w[2,...]*pi))**0.2

HSV = np.dstack((H,S,V))
rgb = hsv_to_rgb(HSV)


fig = plt.figure(figsize=(6,6))
ax = fig.add_axes([0,0,1,1],aspect=1)
ax.axis('off')
plt.imshow(rgb)
#plt.show()
plt.savefig('Icosa_Symmetry.png')

Icaosa