整数bresenham直线算法的演示程序

整数bresenham直线算法是光栅化的标准算法，同时在2D游戏中也可以用于目标直线追踪的算法。

在许多2D游戏中（如老式的RPG），地图环境是离散的，玩家控制的角色的行动方向也是受限的（4个方向或者8个方向）。我们又知道两点之间直线最短，许多情况下，可以利用bresenham直线算法进行目标的追踪。

bresenham直线算法的思想其实并不复杂，下面摘取一些http://cg.sjtu.edu.cn/lecture_site/chap2/mainframe212.htm中的内容来讲解，

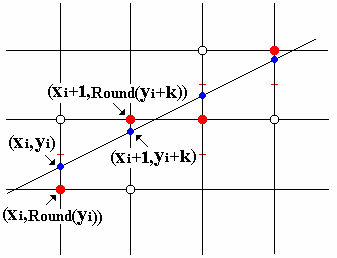
假定直线斜率k在0~1之间。此时，只需考虑x方向每次递增1个单位，决定y方向每次递增0或1。
设直线当前点为(xi,y)，直线当前光栅点为(xi,yi)

则下一个直线的点应为(xi+1,y+k)，下一个直线的光栅点或为右光栅点(xi+1,yi)（y方向递增量0），

或为右上光栅点(xi+1,yi+1)（y方向递增量1）

记直线与它垂直方向最近的下光栅点的误差为d，有：d=(y+k)–yi，且
 0≤d≤1
 当d<0.5：下一个象素应取右光栅点(xi+1,yi)
 当d≥0.5：下一个象素应取右上光栅点(xi+1,yi+1)

可能有人不太明白这一段，其实就是我们要画出一条直线，最终在显示器端是由一个个像素组成的，因为像素也是不连续的，那么我们只能选择离实际直线最近的像素点来进行近似。在2D游戏中也是如此，可以将游戏地图的一个个格子看成像素，那么就是要选择玩家角色需要走过的格子。

令e=d-0.5，关于d的判别式和初值可简化成：
    e的初值e0= -0.5，增量亦为k;
    e<0时，取当前象素(xi,yi)的右方象素(xi+1,yi)；
    e>0时，取当前象素(xi,yi)的右上方象素(xi+1,yi+1)； 
    e=0时，可任取上、下光栅点显示。

Bresenham算法的构思巧妙：它引入动态误差e，当x方向每次递增1个单位，可根据e的符号决定y方向每次递增 0 或 1。
    e<0，y方向不递增
    e>0，y方向递增1
    x方向每次递增1个单位，e = e + k
因为e是相对量，所以当e>0时，表明e的计值将进入下一个参考点（上升一个光栅点），此时须：e = e - 1

整数Bresenham算法
　
上述Bresenham算法在计算直线斜率和误差项时要用到浮点运算和除法，采用整数算术运算和避免除法可以加快算法的速度。
由于上述Bresenham算法中只用到误差项（初值Error =∆y/∆x-0.5）的符号，因此只需作如下的简单变换：
NError = 2*Error*∆x
即可得到整数算法，这使本算法便于硬件实现。

当然目前，这个算法还有一定的局限性，

1.那么如果直线不处于第一象限，需要如何解决？

这个简单，只需要计算∆x和∆y时，加上绝对值就行了。然后根据差值的正负号，确定每次x是+1，还是-1，因为c++中貌似没有提供符号函数sgn（如果有还请告知），需要自行判断一下。

2.如果直线的斜率大于1怎么办？

也就是y方向的差值绝对值要大于x方向的差值绝对值，这里就和斜率小于1时相反了。要往y方向递增，Error则是在x方向累计。

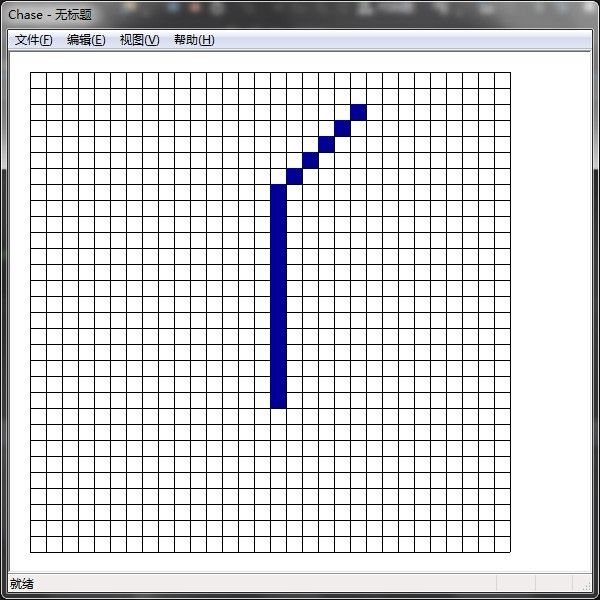
解决了这两个问题，就是一个一般化的整数bresenham直线算法了。昨晚写了一个演示程序，该程序首先画出一个30x30的地图，设置一个起始点和终点，让蓝色格子（可以想象成玩家角色）从起点走到终点，蓝色格子每500ms移动一次。

以下是一些结果：

(2,2) ---> (20,10)

(20,2) --->(15,20)

再让我们看看连算法都称不上的最简单的追踪方法，终点的x大于起点就增加x，对y也是同样。

(2,2) ---> (20,10)

(20,2) --->(15,20)

可以发现傻瓜方法的路线并不美观，并且并不是最短路径，bresenham直线算法就要好不少。

下面是该程序的下载，运用了一些C++ 11的特性，请注意编译器是否支持。

http://download.csdn.net/detail/natsu1211/6625629

因为没写什么注释，顺便稍微说说这个小程序，基于MFC SDI，环境是VS2013。

1.Cmap类

绘制地图，能够自己定义地图大小（先获取窗口的大小，再根据格子数算出每个格子的宽度），并维护了一个share_ptr<CMover>的vector，默认第一个元素是起点，第二个元素是终点。另外维护了一个vector二维数组，对应着绘制出的地图，每次调用AddMover函数就会将数组相应位置置1。这样在重绘时，我们就可以遍历这个二维数组，画出蓝格子。

2.CMover类

代表蓝格子本身，两种追踪方法在这里面实现。

3.View类

增加了InitUpdate消息响应程序，在其中进行timer的初始化。在timer的响应中，调用追踪算法。OnDraw不用说了，用来重绘，我为了省事，地图绘制的函数，物体添加和绘制函数的调用都在这里面完成了，也没使用双缓存。