k近邻法(k-nearest neighbor)
k近邻法(k-nearest neighbor)
标签: 机器学习 Python
1.什么是k近邻法
k近邻法是一种基本的多分类和回归的算法,常常简称为kNN。kNN在李航的《统计学习方法》中的描述如下:
给定一个训练数据集,对新的输入实例,在数据集中找到与该实例最近邻的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类。
可以用一个简单的例子说明一下kNN,二维坐标下有一些点,如图所示:
数据集包含A、B两类数据,具体如下表所示:
| x | y | label |
|---|---|---|
| 0 | 0.03 | A |
| 0.01 | 0 | A |
| 1 | 1.05 | B |
| 1 | 0.95 | B |
现有新的实例(0.1,0.1),要求将其分类。
第一步,计算输入实例和数据集各个数据的欧氏距离:[0.12, 0.01, 1.31, 1.24]
第二步,将计算的距离按照从小到大排序,统计前k个数据的类别,这里假设k为3,则前3个距离最近的数据类为AAB
第三步,将输入实例判断为频率最高的类,本例中A的频率最高(为2),即输入实例是A类数据
2.kNN三要素
kNN的三要素是k,距离度量和分类决策规则。
2.1k
如果选择小的k值,则只有和输入实例比较近的点才会对预测结果产生影响,这样做会导致分类系统的抗噪声能力弱,如果输入实例附近恰好有噪声,分类就极大地可能出错,导致过拟合。
如果选择大的k值,相当于在较大领域进行预测,假设k值和数据集数据的个数一样,则无论输入什么实例,都将分类为数据集中数量最多的类别。
一般情况下,k值选取一个比较小的数值。通常使用交叉验证法选取最优k值。
2.2距离度量
假设数据有n维,则距离的定义为:
这里p>=1,当p=1时,称为曼哈顿距离;当p=2时,称为欧氏距离,一般都使用欧氏距离。
2.3分类决策规则
kNN的分类策略规则是多数表决规则,即前k个最小距离中数量最多的类别决定输入实例的类别。
3.使用kNN对iris数据集中的花进行分类
3.1iris数据集
iris以鸢尾花的特征作为数据来源,常用在分类操作中。该数据集由3种不同类型的鸢尾花的50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的,后两个种类是非线性可分离的。
该数据集包含了5个属性:
& Sepal.Length(花萼长度),单位是cm;
& Sepal.Width(花萼宽度),单位是cm;
& Petal.Length(花瓣长度),单位是cm;
& Petal.Width(花瓣宽度),单位是cm;
& 种类:Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),以及Iris Virginica(维吉尼亚鸢尾)。
由于花瓣宽度变化很小,将其省略后根据前三维数据画出散点图,如下所示:
3.2载入数据
def file2matrix(fileName):
file = open(fileName)
allLines = file.readlines()
row = len(allLines)
dataSet = zeros((row, 4))
labels = []
index = 0
for line in allLines:
line = line.strip()
listFromLine = line.split(',')
dataSet[index, :] = listFromLine[0:4]
labels.append(listFromLine[-1]) #取最后一维为标签
index += 1
return dataSet, labels #数据集和标签分开3.3kNN算法
def kNN(x, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
distance1 = tile(x, (dataSetSize,1)) - dataSet #欧氏距离计算开始
distance2 = distance1 ** 2 #每个元素平方
distance3 = distance2.sum(axis=1) #矩阵每行相加
distance4 = distance3 ** 0.5 #欧氏距离计算结束
sortedIndex = distance4.argsort() #返回从小到大排序的索引
classCount = {}
for i in range (k): #统计前k个数据类的数量
label = labels[sortedIndex[i]]
classCount[label] = classCount.get(label,0) + 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) #从大到小按类别数目排序
return sortedClassCount[0][0]3.3kNN算法测试
def kNN_test():
testRatio = 0.1 #取数据集的前0.1为测试数据
dataSet, labels = file2matrix('irisdata_test.txt')
row = dataSet.shape[0]
testNum = int(row * testRatio)
error = 0.0 #判断错误的个数
for i in range (testNum):
result = kNN(dataSet[i, :], dataSet[testNum:row, :], labels[testNum:row], 3)
print 'the result came back with: %s, the real answer is: %s' % (result, labels[i])
if (result != labels[i]):
error += 1.0
print 'error rate is: %f' % (error/float(testNum))3.4小结
- 输出结果如下:
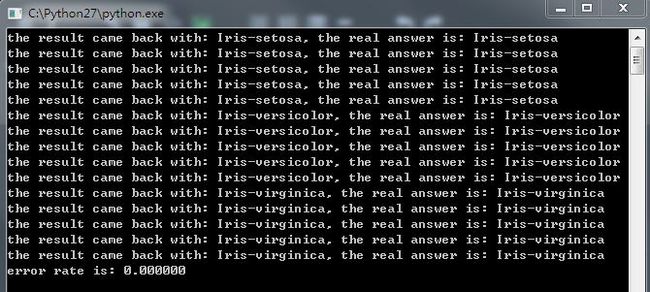
分类效果还是不错的,但是由于后两种花是非线性可分离的,故在交界处的数据很可能分类错误,可以使用SVM等方法将非线性可分离的数据分离 - 当有部分维数的数值较大的时候,会较大的影响距离计算,可以使用 (x−min)/(max−min) 对该维度进行归一化处理
4.总结
- 欢迎在我的GitHub中下载源代码,
MachineLearningAction仓库里面有常见的机器学习算法处理常见数据集的各种实例 - kNN没有明显的学习过程,属于惰性学习方法
- kNN适合于多分类问题,当维数较大时,比SVM快
- k值过小导致对局部数据敏感,抗噪能力差;k值过大,会因为数据集中实例不均衡导致分类出错
- 当数据集较大时,计算量较大,因为每次分类要进行一次全局运算
- kNN多应用于文本分类、模式识别、聚类分析,多分类领域