西南交大2011年第二次暑期集训比赛解题报告

比赛链接 http://acm.swjtu.edu.cn/JudgeOnline/showcontest?contest_id=1096

比赛统计

本场比赛总结

尽管这场比赛参加的人数不多，但是取得的效果我还是挺高兴的，这次的题目应该算是很常规的，每一道题都是考察了一方面的内容，所以我自己认为选题还是很好的，但还是有不足之处，就是缺乏考察数据结构和网络流的题目，等下一次的机会吧

解题分析

A

这一题是改编自2009年合肥赛区（中科大）现场赛的试题，其实我现在都不知道原题是怎么描述的，道听途说而已。方法很简单，打表，其实题目有透露信息的，比如到2009年才发现第47个梅森素数，可见，是可以打表通过的，不过我觉得下午过了的同学想必大多上网去找表了，是吗？“我自以为是”，如果你在合肥现场，你会怎么办呢？在英文版《具体数学》上Page109有梅森素数表可供参考，这题就不多说了。这里贴一个表吧

int A[36] = {2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, \
			127, 521, 607, 1279, 2203, 2281, 3217, 4253, \
			4423, 9689, 9941, 11213, 19937, 21701, 23209, \
			44497, 86243, 110503, 132049, 216091, 756839, \
			859433, 1257787, 1398269, 2976221};

B

这题是经典的树DP，改编自POJ，我们建立二维数组 dp[maxN][2]，其中

dp[ i ][ 0 ]，表示第 i 个人不参加活动时在树结构中最大的和谐值之和

dp[ i ][ 1 ]，表示第 i 个人参加活动时在树结构中最大的和谐值之和

显然

dp[ i ][ 0 ]  = sum { max(0, max(dp[ j ][0],  dp[ j ][ 1 ] )) }

dp[ i ][ 1 ]  = A[i] + sum { max(0,  dp[ j ][ 0 ]) }

#include<cstdio>
#include<cstring>
#include<vector>
#include<iostream>
#include<algorithm>

using namespace std;

const int maxN = 1024;

int N, x, y;
int A[maxN];
vector<int> v[maxN];

int ans;
int dp[maxN][2];

void dfs(int curNode)
{
	dp[curNode][0] = 0;
	dp[curNode][1] = A[curNode];
	ans = max(ans, A[curNode]);
	
	for(int j = 0; j < (int)v[curNode].size(); ++j) {
		if( dp[ v[curNode][j] ][0] == -1 ) {
			dfs( v[curNode][j] );
			
			dp[curNode][1] += max(0, dp[v[curNode][j]][0]);
			dp[curNode][0] += max(0, max(dp[v[curNode][j]][0], dp[v[curNode][j]][1]));
			
			ans = max(ans, max(dp[curNode][0], dp[curNode][1]));
		}
	}
}

int main()
{
	//freopen("data.in", "r", stdin);
	while( scanf("%d", &N) == 1 ) {
		for(int i = 1; i <= N && scanf("%d", A + i); ++i) v[i].clear(); 
		for(int i = 1; i < N && scanf("%d %d", &x, &y); ++i) v[x].push_back(y), v[y].push_back(x); 
		
		memset(dp, -1, sizeof(dp));
		ans = 0; dfs(1);
		
		printf("%d\n", ans);
	}
	return 0;
}

C

这题是很好的 dfs 搜索题，思想就是模拟栈了，这里注意到，因为最大才16，所以可以用位运算保存状态，在状态存储标记的时候，如果某一位为 ‘1’，表示离开，否则为进来，这样做的好处方便我们可以肯定，满足条件的最后一位一定是’1‘，而如果反过来表示，则最后一位一定是’0‘，但是，你并不知道它是不是表示离开这个状态。

#include<cstdio>
#include<cstring>
 
typedef long long llong;
 
const int maxn = 20 + 2;
 
int N, K;
int A[maxn], L[maxn];
int tot_ans;
 
void dfs(llong status, int posA, int posL, int posQ, int Q[]) {
	if(tot_ans == 16) return ;
	
	if(status & (1LL << (2 * N - 1))) {
		++tot_ans;
		for(int i = 0; i < (N << 1); ++i) {
			if(status & (1LL << i) ) putchar('L');
			else putchar('A');
		}
		puts("");
		return ;
	} // it has N A's and N L's, assume '1' -> L and '0' -> 'A'
 
	// if we can do 'A'
	if(posA < N) {
		int newQ[maxn << 1];
		memcpy(newQ, Q, posQ * sizeof(int));
		newQ[posQ] = A[posA];
 
		dfs(status, posA + 1, posL, posQ + 1, newQ);
	}

	// if we can do 'L'
	if(posL < N && Q[posQ - 1] == L[posL]) {
		dfs(status | (1LL << (posA + posL)), posA, posL + 1, posQ - 1, Q);
	}
}
 
int main() {
    //freopen("data.in", "r", stdin);
    //freopen("data.out", "w", stdout);
	int Q[maxn << 1]; int sgn = 0;
	while( scanf("%d%d", &N, &K) == 2 ) {
        if( sgn ) puts("");
        else sgn = 1;
        
		for(int i = 0; i < N; ++i) scanf("%d", A + i);
		for(int i = 0; i < N; ++i) scanf("%d", L + i);
 
		int idx_A = 0, idx_L = 0, idx_Q = 0;
		Q[idx_Q++] = A[idx_A++];
 
		llong status = 0;
		tot_ans = 0;
		dfs(status, idx_A, idx_L, idx_Q, Q);
 
		if( tot_ans == 0 ) puts("Impossible");
	}
	return 0;
}

D

模拟题，这题没什么好说了，其实，一开始这一题我一直担心会出错，因为这题没有标程，测试数据是我手工出的，在 Python 测了好几遍，赛后才写了个标程，还好测试数据没有问题。

#include<cstdio>
#include<cstring>

const int maxN = 100 + 2;

typedef long long i64d;

char str[maxN];

int main()
{
	//freopen("data.in", "r", stdin);
	static int idx = 0; bool sgn = 1, okX;
	i64d preVal = 0, X, Y, sgnX, sgnY;
	while( scanf("%s", str) == 1 ) {
		if( sgn ) printf("Case #%d:\n", ++idx), sgn = 0;
		if( !strcmp(str, "exit()")) { sgn = 1; preVal = 0; continue; }
		
		X = -1LL; Y = 0LL; okX = 0;
		sgnX = sgnY = 1LL;
		for(int i = 0; str[i]; ++i) {
			if( !okX ) {
				if( (str[i] == '+' || str[i] == '-') && X != -1LL ) { okX = 1; goto LP; }
				else if( str[i] == '+' ) continue;
				else if( str[i] == '-' ) sgnX *= -1LL;
				else if( str[i] == '_' ) X = preVal, okX = 1;
				else {
					if( X == -1LL ) X = 0;
					X = 10LL * X + (str[i] - '0');
				}
			} else { LP:
				if( str[i] == '+' ) continue;
				else if( str[i] == '-' ) sgnY *= -1;
				else if( str[i] == '_' ) Y = preVal;
				else Y = 10LL * Y + (str[i] - '0');
			}
		}
		
		//printf("%I64d + %I64d\n", X * sgnX, Y * sgnY);
		preVal = sgnX * X + sgnY * Y;
		
		printf("%I64d\n", preVal);
	}
	return 0;
}

以上四题就是我自己想让大家做下的题目了，没有 AK 的。

本来以为黄海与老师也出了题目，后来告诉我说时间紧，就没有出题目，没办法，我总不能让大家就只做四道吧，所以选了3题E、F、G放上去了，这三题都是 csc2009 的比赛题，感觉挺好的，也推荐大家做做吧。

E

题目大意

题目改编自网上一个flash游戏“魔塔”。

在魔塔游戏里面，公主被囚禁在塔里，塔是分了很多层的，此题简化了这个游戏，只有1层。在塔里面分布着各种各样的东西，有怪兽，有生命水（喝了可以增加生命值），有不同颜色的门和不同颜色的钥匙。这4样东西的总和最多为12个。每遇到一个怪兽，怪兽有攻击力，如果英雄的生命值大于攻击力，则可以打败这个怪兽继续前进，问最少需要走多少步，英雄能救出公主。且输出步骤，若有多个解，输出逻辑顺序最小的一个，以上左下右的顺序作为优先级。

思路

定义状态

题目给出东西的总和上限是12，塔的大小是12*12因此可定义状态如下：

生命值，各种颜色的钥匙总数，坐标，东西的取得状态（包括打败怪兽）。

再仔细分析可以知道，由于生命值和各种颜色的钥匙总数可以根据东西取得的状态进行计算，因此，状态简化为以下2样：

坐标，东西取得状态。

因此，总状态数为12*12*2^12.bfs即可。

定义结构体

搜索中的结点

struct Node
{
  int x, y, pre;
  int s, step;
  Node(){}
  Node( int xx, int yy, int p, int ss, int st ):x(xx),y(yy),pre(p),s(ss),step(st){} 
};

各样东西的结构体

struct element
{
  char kind;
  int val;
};

注意的问题

必须注意，当一个是钥匙或是一个怪兽的地方，如果状态中已经记录过了，就不需要再次判断，否则就不对了

其次，注意扩展的时候，按题目所给的优先级顺序扩展，本题不是SPJ，所以只有1个解。如果不按题目所给的顺序扩展，当不止1个解的时候，路径就不对了

F

题目大意

直线上有n个格子,0,1,…,n-1.现在有两个一样的棋子放在(0,1)位置.现在每步可以按跳棋的规则移动一个棋子,问至少多少步可以将两个棋子移动到(n-2,n-1)或(n-1,n-2)位置

题目分析

BFS

如果当前状态为(x, y)，而且不妨假设x < y，那么，下一步的状态就可以是： (x + 1, y), (x - 1, y), (x, y + 1), (x, y  - 1), (x - (y - x), x), (y, y + (y - x))，当然你需要判断其合法性

值得注意的是，你不要每一次都BFS，这样你会TLE，你可以一次遍历 N = 1000的情况，然后每次直接 O( 1 )输出结果就可以了，至于这样做的可行性，你可以自己想想

#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

const int maxN = 1024;

struct node
{
	int x, y;
	
	node() {}
	node(int _x, int _y) : x(_x), y(_y) {}
};

queue<node> q;

int N;
int dp[maxN][maxN];

void bfs()
{
	while( !q.empty() ) q.pop();
	
	dp[0][1] = 1;
	q.push( node(0, 1) );
	
	node tmp, cur; int x, y;
	while( !q.empty() ) {
		tmp = q.front(); q.pop();
		
		x = tmp.x, y = tmp.y;

		if( x - 1 >= 0 && !dp[x - 1][y] ) {
			dp[x - 1][y] = dp[x][y] + 1; 
			cur = tmp; cur.x -= 1;
			q.push( cur );
		}
		
		if( x + 1 < y && !dp[x + 1][y] ) {
			dp[x + 1][y] = dp[x][y] + 1; 
			cur = tmp; cur.x += 1;
			q.push( cur );
		}
		
		if( y - 1 > x && !dp[x][y - 1] ) {
			dp[x][y - 1] = dp[x][y] + 1; 
			cur = tmp; cur.y -= 1;
			q.push( cur );
		}
		
		if( y + 1 < N && !dp[x][y + 1] ) {
			dp[x][y + 1] = dp[x][y] + 1; 
			cur = tmp; cur.y += 1;
			q.push( cur );
		}
		
		if( 2 * y - x < N && !dp[y][2 * y - x] ) {
			dp[y][2 * y - x] = dp[x][y] + 1; 
			cur.x = y; cur.y = 2 * y - x;
			q.push( cur );
		}
		
		if( 2 * x - y >= 0 && !dp[2 * x - y][x] ) {
			dp[2 * x - y][x] = dp[x][y] + 1;
			cur.x = 2 * x - y; cur.y = x;
			q.push( cur );
		}
	}
}

int main()
{
	//freopen("data.in", "r", stdin);
	N = 1000;
	memset(dp, 0, sizeof(dp));
	bfs();
	
	int nT; scanf("%d", &nT);
	while( (nT --) > 0 ) {
		scanf("%d", &N);
		
		printf("%d\n", dp[N - 2][N - 1] - 1);
	}
	return 0;
}

G

数学模型

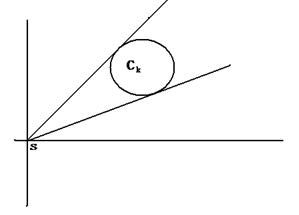
给定一点s，圆Ck，圆CI 。

问是否存在由s引出的一条射线，使得该射线经过Ck ，但不经过Cl 。（这里“经过”定义为相交或相切）

若设s即为坐标原点，则模型简化为：

是否存在由原点（0，0）引出的一条射线，使得该射线经过Ck ，但不经过CI 。

分析

过原点作两条射线相切于Ck

显然如果CI与这两射线没有交点，则问题答案为“Yes”，注意，是射线方向上无交点

考虑有交点的情况

Question： CI在何位置时，答案是“No”？

如图所示，可以看出，当且仅当CI与两射线不同时“经过”时，答案是“Yes”。

如此一来，只要知道如下两个问题求解方法：

（1）如何判断射线是否“经过”给定圆

（2）如何求过给定点与圆的切线以及切点

对于问题（1）

可以将射线所在的直线方程代入圆方程，对得到的二次方程求解

有解的话，还需判断是否在射线方向上，推荐使用判断向量乘积符号的方法

对于问题（2）

可以利用勾股定理以及直线倾斜角的角度关系求得